Random

Partial Differentiation

Usage

If you have a function of two variables such that $p=f(q,r)\,$

then the following equation is true in general

{\frac {dp}{dx}}={\frac {\partial p}{\partial q}}{\frac {dq}{dx}}+{\frac {\partial p}{\partial r}}{\frac {dr}{dx}}

this allows you to calculate the rate of change of $p$ given the rate of change of $q$ and $r$ . For example, in the case of a cone

V={\frac {\pi r^{2}h}{3}}

{\frac {\partial V}{\partial r}}={\frac {2\pi rh}{3}}

{\frac {\partial V}{\partial h}}={\frac {2\pi r^{2}}{3}}

this means that the following is true

{\frac {dV}{dt}}={\frac {2\pi r}{3}}{\bigg (}h{\frac {dr}{dt}}+r{\frac {dh}{dt}}{\bigg )}

Ref Desk Q's

electrons

I asked a similar question this yesterday, though this one seems much more complicated to me. I will go through my calucaltions so far, so if there are any errors, you can help me rectify them.

If you have n electrons distributed evenly around a circle radius r, distance x from another electron, what is the force of repulsion experienced by the electron not on the circle from the circle of electrons. Electrostatic repulsion is a inverse square law, and the coefficent of electrostatic force can be considered as k.

r = radius (OA, OC)
x = CY
y = OB
a = AY
α = AOY
β = BAY

using cosine rule; $a={\sqrt {x^{2}+(x+r)^{2}-2r(r+x)\cos \alpha }}$ so the force, being an inverse square is; $F={\frac {k}{x^{2}+(x+r)^{2}-2r(r+x)\cos \alpha }}$ now, seeing as always in the circle the components in y-direction will cancel, we can consider only those in the x-direction in order to caluclate a resultant force we need to consider only the x-directions components, to find this consider the triangle ABY, the angle β and distance OB are neccesary. using sine rule. $y=-r\cos(\alpha )\,$
therefore using sine rule,
$\sin \beta ={\frac {r-r\cos(\alpha )+x}{\sqrt {x^{2}+(x+r)^{2}-2r(r+x)\cos \alpha }}}$
so the x direction component of F, or Fsinβ is;
${\mathit {F_{x}}}={\frac {k(r-r\cos(\alpha )+x)}{{\big [}x^{2}+(x+r)^{2}-2r(r+x)\cos \alpha {\big ]}^{\frac {3}{2}}}}$

So to consider all the electrons; then $\alpha ={\frac {2\pi {\mathit {k}}}{N}}$ where N number of electrons. and k varies from 1 to N. Therfore a sum of all the forces would be.

${\mathit {F_{total}}}={\frac {k}{N}}\sum _{k=1}^{N}{\bigg [}{\frac {r-r\cos({\frac {2\pi k}{N}})+x}{{\big [}x^{2}+(x+r)^{2}-2r(r+x)\cos({\frac {2\pi k}{N}}){\big ]}^{\frac {3}{2}}}}{\bigg ]}$

Now this is it, I really need some help simplifying this massive mess, and like yesterday I really need the summation series out of the equation if that's possible. Thank you.

data handling

$\mathrm {R} (\parallel )\;\;\mathrm {F} =\mathrm {m} _{1}\mathrm {g} \sin \theta -\mathrm {m} _{2}\mathrm {g} \,\!$

$\mathrm {F} =\mathrm {ma} \,\!$

$\mathrm {ma} =\mathrm {m} _{1}\mathrm {g} \sin \theta -\mathrm {m} _{2}\mathrm {g} \,\!$

$(\mathrm {m} _{1}+\mathrm {m} _{2})\mathrm {a} =\mathrm {m} _{1}\mathrm {g} \sin \theta -\mathrm {m} _{2}\mathrm {g} \,\!$

$\mathrm {a} ={\frac {\mathrm {m} _{1}\mathrm {g} \sin \theta -\mathrm {m} _{2}\mathrm {g} }{\mathrm {m} _{1}+\mathrm {m} _{2}}}$

$\mathrm {m} _{1}=1.000,\;\;\mathrm {m} _{2}=0.526,\;\;\mathrm {g} =9.8$

$\mathrm {v} ={\frac {\Delta \mathrm {d} }{\Delta \mathrm {t} }}$

$\mathrm {v} ^{2}=\mathrm {u} ^{2}+2\mathrm {a} \mathrm {s} \,\!$

$\mathrm {v} ^{2}-\mathrm {u} ^{2}=2\mathrm {a} \mathrm {s} \,\!$

${\frac {\mathrm {v} ^{2}-\mathrm {u} ^{2}}{2\mathrm {s} }}=\mathrm {a} \,\!$

$\mathrm {u} =0,\;\;\mathrm {s} =0.25$

$\mathrm {F} _{t}=\,\!$

$\mathrm {R} (\parallel )\;\;\;\mathrm {m} _{1}\mathrm {g} \sin \theta -(\mathrm {m} _{1}+\mathrm {m} _{2})a-\mathrm {m} _{2}\mathrm {g} =\mathrm {F} _{t}\,\!$

$\mathrm {m} _{2}\mathrm {g} -(\mathrm {m} _{1}+\mathrm {m} _{2})a-\mathrm {m} _{1}\mathrm {g} \sin \theta =\mathrm {F} _{t}\,\!$

$\mathrm {m} _{2}\mathrm {g} =\mathrm {m} _{1}\mathrm {g} \sin \theta \,\!$

$0.526=\sin \theta \,\!$

$\theta =31.736\,\!$

$\Delta \mathrm {h} =0.25\sin \theta \,\!$

$\mathrm {gpe} =\mathrm {m} \cdot \mathrm {g} \cdot \mathrm {h} \,\!$

$\Delta \mathrm {gpe} _{trolley}=0.25\sin \theta \times 9.8\times 1\,\!$

$\Delta \mathrm {gpe} _{mass}=0.25\times 9.8\times 0.526\,\!$

$|\Delta \mathrm {gpe} _{mass}-\Delta \mathrm {gpe} _{trolley}|=\mathrm {ke} +\mathrm {energy} \;\mathrm {lost} \,\!$

sense proj

(1*1.1*10^(-6))/(pi*((0.193*10^(-3))/2)^2)

$R={\frac {\rho \times L}{A}}$

$R={\frac {1\times 1.1\times 10^{-6}}{\pi \times ({\frac {0.193\times 10^{-3}}{2}})^{2}}}$

Silicon proj

known

\rho _{p}\ \mathbf {R} \mathbf {e} \mathbf {s} \mathbf {i} \mathbf {s} \mathbf {t} \mathbf {i} \mathbf {v} \mathbf {i} \mathbf {t} \mathbf {y} \ \mathbf {o} \mathbf {f} \ \mathbf {P} \mathbf {u} \mathbf {r} \mathbf {e} \mathbf {\ } \mathbf {S} \mathbf {i} \mathbf {l} \mathbf {i} \mathbf {c} \mathbf {o} \mathbf {n} \ =10^{6}\Omega \mathbf {m} =10\ \mathbf {m} \mathbf {i} \mathbf {l} \mathbf {l} \mathbf {i} \mathbf {o} \mathbf {n} \ \Omega \mathbf {m}

\rho _{d}\ \mathbf {R} \mathbf {e} \mathbf {s} \mathbf {i} \mathbf {s} \mathbf {t} \mathbf {i} \mathbf {v} \mathbf {i} \mathbf {t} \mathbf {y} \ \mathbf {o} \mathbf {f} \ \mathbf {D} \mathbf {o} \mathbf {p} \mathbf {e} \mathbf {d} \ \mathbf {S} \mathbf {i} \mathbf {l} \mathbf {i} \mathbf {c} \mathbf {o} \mathbf {n} \ =10^{2}\Omega \mathbf {m} =10\ \mathbf {t} \mathbf {h} \mathbf {o} \mathbf {u} \mathbf {s} \mathbf {a} \mathbf {n} \mathbf {d} \ \Omega \mathbf {m}

h\ \ \mathbf {H} \mathbf {e} \mathbf {i} \mathbf {g} \mathbf {h} \mathbf {t} =1\mathbf {m} \mathbf {m} =10^{-3}\mathbf {m}

w\ \ \mathbf {W} \mathbf {i} \mathbf {d} \mathbf {t} \mathbf {h} =1\mathbf {m} \mathbf {m} =10^{-3}\mathbf {m}

l\ \ \mathbf {L} \mathbf {e} \mathbf {n} \mathbf {g} \mathbf {t} \mathbf {h} =5\mathbf {m} \mathbf {m} =5\times 10^{-3}\mathbf {m}

known

\rho ={{RA} \over l}

A=hw\,

therfore

{\frac {\rho l}{hw}}=R

for pure

{\frac {10^{6}\times 5\times 10^{-3}}{10^{-3}\times 10^{-3}}}=R

{\frac {10^{6}\times 5}{10^{-3}}}=R

10^{9}\times 5=R

R=5\times 10^{9}\Omega

for doped

{\frac {10^{2}\times 5\times 10^{-3}}{10^{-3}\times 10^{-3}}}=R

{\frac {10^{2}\times 5}{10^{-3}}}=R

10^{5}\times 5=R

R=5\times 10^{5}\Omega

Maths Problem

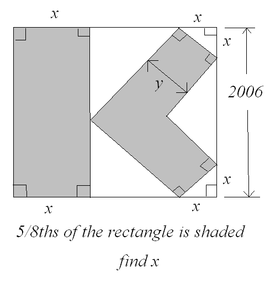
Ok well I encountered this problem (I added the y to simplify some calculations a bit, but otherwise its exactly the same information i got). I tried to solve but I wasnt sure wether I had done it correctly. So I thought I'd post here for someone to maybe review it and find the faults or confirm wether its correct. So heres what I went about doing. I numbered the steps for reference in your replies.

Well firstly isnce the triangles in the corners have x on both sides, we can assume they are isoceles right angled triangles, therefore the angles are 90, 45, and 45, thus meaning that all the angles in any of the shapes in this case are either 45 or 90.
$y={\sqrt {x^{2}+x^{2}}}$ (pythagorus)
The white triangle in the centre of the right hand edge is (assuming the two sides identical in length are variable z)
1. $2006-2x=z^{2}+z^{2}$ (pythagorus)
2. $2006-2x=2z^{2}$
3. ${\frac {2006-2x}{2}}=z^{2}$
4. ${\sqrt {\frac {2006-2x}{2}}}=z$
the L shape can now be divided into 3 segments, one square in the centre which is $y^{2}$ $y^{2}$ , and 2 identical rectangles which are y by z. And as such the grey area consists of
- $2(y({\sqrt {\frac {2006-2x}{2}}}))+y^{2}$
As such the entire grey area works out to equal this when the left part of the shape is included
- $2({\sqrt {x^{2}+x^{2}}})({\sqrt {\frac {2006-2x}{2}}})+({\sqrt {x^{2}+x^{2}}})^{2}+2006x$
Therefore, the entire size of the shape should equal
1. $8({\frac {2({\sqrt {2x^{2}}})({\sqrt {\frac {2006-2x}{2}}})+2x^{2}+2006x}{5}})$
2. $8({\frac {2(x{\sqrt {2}})({\sqrt {\frac {2006-2x}{2}}})+2x^{2}+2006x}{5}})$
3. $8({\frac {2x({\sqrt {2006-2x}})+2x^{2}+2006x}{5}})$
The two triangles with their sides against the x by 2006 shaded areas two identiacal sides can be calculated (assuming the two sides identical in length are variable a)
1. $(z+y)^{2}=a^{2}+a^{2}$
2. $(z+y)^{2}=2a^{2}$
3. ${\frac {(z+y)^{2}}{2}}=a^{2}$
4. ${\sqrt {\frac {(z+y)^{2}}{2}}}=a$
Substituting in the other formulae, to give in terms of x leaves
- ${\sqrt {\frac {({\sqrt {\frac {2006-2x}{2}}}+2(x{\sqrt {2}}))^{2}}{2}}}=a$
So the formula for the entire square equals
- $2006({\sqrt {\frac {({\sqrt {\frac {2006-2x}{2}}}+2(x{\sqrt {2}}))^{2}}{2}}})+2x)$
So now we have 2 formula for the entire shape, so we can substitute them together
- $2006({\sqrt {\frac {({\sqrt {\frac {2006-2x}{2}}}+2(x{\sqrt {2}}))^{2}}{2}}})+2x)=8({\frac {2x({\sqrt {2006-2x}})+2x^{2}+2006x}{5}})$

Unfortunately this is where I got stuck. So if anyone knows where to go from here... The help would be appreciated. Philc _T^E_C^I 21:04, 10 September 2006 (UTC)

Space

Russian Launch Vehicles Template

Russian Launch Vehicles

R-7 Semyorka • R-12 Cosmos • R-14 Cosmos • D-1 Proton (UR-500 Proton) • N-1 (SL-15, G-1e) • UR-700 • R-56 (RK-100) •

[1] Angara Angara-2 Angara-100 Angara-3 Avrora (see R-7) Baikal Berkut Bulat Burlak Cosmos (see R-12, R-14) Dnepr Dvina Edinstvo Energia Energia-M Energia-2 Enisei Faeton-2/2T Fregat complex (see Grom) Grom Groza Ishim Kvant Luna (see R-7A) Molnia (see R-7A) N1/L3 Neitron (see Energia-M) Neva Priboi Prizuv (see UR-100) R-3 R-7A/Sputnik R-7A/ Luna/Vostok R-7A/Vostok-2 R-7A/Vostok-2M R-7A/ R-7A/Molnia R-7A/Voskhod R-7A/Soyuz R-7A/Soyuz-U R-7A/Soyuz-U2 R-7A/Soyuz-U2 R-7A/Soyuz-2 R-7A/Yamal R-7A/Avrora R-7A/Onega R-7A/Soyuz-2-3 R-7A/Soyuz-3 R-12/Cosmos R-12/Cosmos-2 R-14/Cosmos-1 R-14/Cosmos-3 R-14/Cosmos-3M R-14/Cosmos-U R-14/Vzlet R-16/Tsyklon-1 R-16-based R-26-based OR-36-based R-36-based R-36/Tsyklon-2A R-36/Tsyklon-3 (Tsyklon-M) R-36/Tsyklon-2 R-36/Tsyklon-4 (Mayak) R-56/RK-100 Rif-MA Riksha RLA-125 (Groza) Rockot Shtil-1N Shtil-2N Shtil-3A Shtil-3N Soyuz (see R-7A) Space Clipper Start-1 Start Surf Tsyklon (see R-36) Strela UR-200 UR-500K Proton UR-500K-L1, L1P UR-500KM UR-700 UR-700M UR-900 UR-1000 Volna Voskhod (see R-7A) Vostok (see R-7A) Vulkan Vysota Vzlet (see R-14) YaKhR-2 Yamal (see R-7A) Zenit-based Zenit-based Zenit-2 Zenit-3SL Zub

Deletion

All FIFA World Cup squad lists

August 11, 2006 21:00
	Delete	4–2	Keep	venue

Copa Libertadores de América

Year	Final			Semifinalists
Year	Winner	Score	Runner-up	Semifinalists
1960 Details	Peñarol Uruguay	1 - 0 1 - 1 Aggregate 2 - 1	Olimpia Paraguay	San Lorenzo Argentina	Millonarios Colombia
1961 Details	Peñarol Uruguay	1 - 0 1 - 1 Aggregate 2 - 1	Palmeiras Brazil	Olimpia Paraguay	Independiente de Santa Fe Colombia
1962 Details	Santos F.C. Brazil	1 - 2 3 - 2 Aggregate 3 - 0	Peñarol Uruguay	Universidad Católica Chile	Nacional Uruguay
1963 Details	Santos F.C. Brazil	3 - 2 2 - 1 Aggregate 5 - 3	Boca Juniors Argentina	Botafogo Brazil	Peñarol Uruguay
1964 Details	Independiente Argentina	0 - 0 1 - 0 Aggregate 1 - 0	Nacional Uruguay	Santos F.C. Brazil	Colo-Colo Chile
1965 Details	Independiente Argentina	1 - 0 1 - 3 Aggregate 4 - 1	Peñarol Uruguay	Santos F.C. Brazil	Boca Juniors Argentina
1966 Details	Peñarol Uruguay	2 - 0 2 - 3 Aggregate 4 - 2	River Plate Argentina	Independiente Argentina	Universidad Católica Chile
1967 Details	Racing Club Argentina	0 - 0 0 - 0 Aggregate 2 - 1	Nacional Uruguay	Universitario Peru	Cruzeiro Brazil
1968 Details	Estudiantes L.P. Argentina	2 - 1 1 - 3 Aggregate 2 - 0	Palmeiras Brazil	Peñarol Uruguay	Racing Club Argentina
1969 Details	Estudiantes L.P. Argentina	1 - 0 2 - 0 Aggregate 3 - 0	Nacional Uruguay	Peñarol Uruguay	Universidad Católica Chile
1970 Details	Estudiantes L.P. Argentina	1 - 0 0 - 0 Aggregate 1 - 0	Peñarol Uruguay	Universidad de Chile Chile	River Plate Argentina
1971 Details	Nacional Uruguay	1 - 0 0 - 1 Aggregate 2 - 0	Estudiantes L.P. Argentina	Palmeiras Brazil	Barcelona (Guayaquil) Ecuador
1972 Details	Independiente Argentina	0 - 0 2 - 1 Aggregate 2 - 1	Universitario Peru	Nacional Uruguay	São Paulo Brazil
1973 Details	Independiente Argentina	1 - 1 0 - 0 Aggregate 2 - 1	Colo-Colo Chile	San Lorenzo Argentina	Cerro Porteño Paraguay
1974 Details	Independiente Argentina	1 - 2 2 - 0 Aggregate 1 - 0	São Paulo Brazil	Peñarol Uruguay	Millonarios Colombia
1975 Details	Independiente Argentina	0 - 1 3 - 1 Aggregate 2 - 0	Unión Española Chile	Rosario Central Argentina	Universitario Peru
1976 Details	Cruzeiro Brazil	4 - 1 1 - 2 Aggregate 3 - 2	River Plate Argentina	LDU (Quito) Ecuador	Independiente Argentina
1977 Details	Boca Juniors Argentina	1 - 0 0 - 1 Aggregate 0 - 0 Penalties 5-4	Cruzeiro Brazil	Deportivo Cali Colombia	Internacional Brazil
1978 Details	Boca Juniors Argentina	0 - 0 4 - 0 Aggregate 4 - 0	Deportivo Cali Colombia	River Plate Argentina	Cerro Porteño Paraguay
1979 Details	Olimpia Paraguay	2 - 0 0 - 0 Aggregate 2 - 0	Boca Juniors Argentina	Independiente Argentina	Guarani Brazil
1980 Details	Nacional Uruguay	2 - 0 0 - 0 Aggregate 2 - 0	Internacional Brazil	Olimpia Paraguay	America de Cali Colombia
1981 Details	Flamengo Brazil	2 - 1 0 - 1 Aggregate 2 - 0	Cobreloa Chile	Deportivo Cali Colombia	Nacional Uruguay
1982 Details	Peñarol Uruguay	0 - 0 1 - 0 Aggregate 1 - 0	Cobreloa Chile	Flamengo Brazil	Olimpia Paraguay
1983 Details	Grêmio Brazil	1 - 1 2 - 1 Aggregate 3 - 2	Peñarol Uruguay	Nacional Uruguay	Estudiantes L.P. Argentina
1984 Details	Independiente Argentina	1 - 0 0 - 0 Aggregate 1 - 0	Grêmio Brazil	Nacional Uruguay	Flamengo Brazil
1985 Details	Argentinos Juniors Argentina	1 - 0 0 - 1 Aggregate 1 - 1 Penalties 5-4	America de Cali Colombia	El Nacional Ecuador	Independiente Argentina
1986 Details	River Plate Argentina	2 - 1 1 - 0 Aggregate 3 - 1	America de Cali Colombia	Argentinos Juniors Argentina	Olimpia Paraguay
1987 Details	Peñarol Uruguay	0 - 2 2 - 1 Aggregate 2 - 0	America de Cali Colombia	Cobreloa Chile	River Plate Argentina
1988 Details	Nacional Uruguay	0 - 1 3 - 0 Aggregate 3 - 1	Newell's Old Boys Argentina	America de Cali Colombia	San Lorenzo Argentina
1989 Details	Atlético Nacional Colombia	2 - 0 0 - 2 Aggregate 2 - 2 Penalties 5-4	Olimpia Paraguay	Danubio Uruguay	Internacional Brazil
1990 Details	Olimpia Paraguay	2 - 0 1 - 1 Aggregate 3 - 1	Barcelona (Guayaquil) Ecuador	River Plate Argentina	Atlético Nacional Colombia
1991 Details	Colo-Colo Chile	0 - 0 3 - 0 Aggregate 3 - 0	Olimpia Paraguay	Atlético Nacional Colombia	Boca Juniors Argentina
1992 Details	São Paulo Brazil	1 - 0 0 - 1 Aggregate 1 - 1 Penalties 3-2	Newell's Old Boys Argentina	America de Cali Colombia	Barcelona (Guayaquil) Ecuador
1993 Details	São Paulo Brazil	5 - 1 0 - 2 Aggregate 5 - 3	Universidad Católica Chile	America de Cali Colombia	Cerro Porteño Paraguay
1994 Details	Vélez Sársfield Argentina	0 - 1 1 - 0 Aggregate 1 - 1 Penalties 5-3	São Paulo Brazil	Atlético Junior Colombia	Olimpia Paraguay
1995 Details	Grêmio Brazil	3 - 1 1 - 1 Aggregate 4 - 2	Atlético Nacional Colombia	River Plate Argentina	Emelec Ecuador
1996 Details	River Plate Argentina	0 - 1 2 - 0 Aggregate 2 - 1	America de Cali Colombia	Grêmio Brazil	Universidad de Chile Chile
1997 Details	Cruzeiro Brazil	0 - 0 1 - 0 Aggregate 1 - 0	Sporting Cristal Peru	Colo-Colo Chile	Racing Club Argentina
1998 Details	Vasco da Gama Brazil	2 - 0 2 - 1 Aggregate 4 - 1	Barcelona (Guayaquil) Ecuador	Cerro Porteño Paraguay	River Plate Argentina
1999 Details	Palmeiras Brazil	0 - 1 2 - 1 Aggregate 2 - 2 Penalties 4-3	Deportivo Cali Colombia	River Plate Argentina	Cerro Porteño Paraguay
2000 Details	Boca Juniors Argentina	2 - 2 0 - 0 Aggregate 2 - 2 Penalties 4-3	Palmeiras Brazil	Corinthians Brazil	Club América Mexico
2001 Details	Boca Juniors Argentina	1 - 0 0 - 1 Aggregate 1 - 1 Penalties 3-1	Cruz Azul Mexico	Palmeiras Brazil	Rosario Central Argentina
2002 Details	Olimpia Paraguay	0 - 1 2 - 1 Aggregate 2 - 2 Penalties 4-2	São Caetano Brazil	Club América Mexico	Grêmio Brazil
2003 Details	Boca Juniors Argentina	2 - 0 3 - 1 Aggregate 5 - 1	Santos F.C. Brazil	Independiente Medellín Colombia	America de Cali Colombia
2004 Details	Once Caldas Colombia	0 - 0 1 - 1 Aggregate 1 - 1 Penalties 2-0	Boca Juniors Argentina	River Plate Argentina	São Paulo Brazil
2005 Details	São Paulo Brazil	1 - 1 4 - 0 Aggregate 5 - 1	Atlético Paranaense Brazil	River Plate Argentina	Guadalajara Mexico
2006 Details

CAF Champions League

Champions League Finals

Season	Winner	Score	Runner-up	Group stage runners-up Note: Before 2001 two groups were used instead of semifinals, the winners of each group passed to the finals, shown are the runners up of each group
1997 Details	Raja Casablanca (Morocco)	1st leg: 0-1 2nd leg: 1-0 Penalties: 5-4	Obuasi Goldfields (Ghana)	USM Alger (Algeria)	Al-Zamalek (Egypt)
1998 Details	ASEC Abidjan (Côte d'Ivoire)	1st leg: 4-2 2nd leg: 0-0	Dynamos (Zimbabwe)	Manning Rangers (RSA)	Hearts of Oak (Ghana)
1999 Details	Raja Casablanca (Morocco)	1st leg: 0-0 2nd leg: 0-0 Penalties: 4-3	Espérance (Tunisia)	Al-Ahly (Egypt)	ASEC Abidjan (Côte d'Ivoire)
2000 Details	Hearts of Oak (Ghana)	1st leg: 2-1 2nd leg: 3-1	Espérance (Tunisia)	Al-Ahly (Egypt)	Mamelodi Sundowns (RSA)
Season	Winner	Score	Runner-up	Losing Semifinalists
Season	Winner	Score	Runner-up	lost to eventual winner	lost to eventual runner-up
2001 Details	Al-Ahly (Egypt)	1st leg: 1-1 2nd leg: 3-0	Mamelodi Sundowns (RSA)	Espérance (Tunisia)	Atlético Petróleos Luanda (Angola)
2002 Details	Al-Zamalek (Egypt)	1st leg: 0-0 2nd leg: 1-0	Raja Casablanca (Morocco)	TP Mazembe (DRC)	ASEC Abidjan (Côte d'Ivoire)
2003 Details	Enyimba (Nigeria)	1st leg: 2-0 2nd leg: 0-1	Ismaily SC (Egypt)	USM Alger (Algeria)	Espérance (Tunisia)
2004 Details	Enyimba (Nigeria)	1st leg: 1-2 2nd leg: 2-1 Penalties: 5-3	Étoile Sahel (Tunisia)	Espérance (Tunisia)	ASC Jeanne d'Arc (Senegal)
2005 Details	Al-Ahly (Egypt)	1st leg: 0-0 2nd leg: 3-0	Étoile Sahel (Tunisia)	Al-Zamalek (Egypt)	Raja Casablanca (Morocco)
2006 Details

SAM76

The SAM76 language is a list and string processor that is uniquely suited for a variety of interactive and user-directed applications, including artificial intelligence programming, and permits a high portability from machine to machine. The SAM76 language shares certain features in common with the LISP and Forth programming languages and, pointing to the future of multiuser or concurrent systems operation, with the SHELL programming language of the UNIX operating system.

Claude Kagan, the language's developer, sought to combine within a single interpretive processor, the characteristics of two different string and general-purpose macro generators and the provisions to embed multiple infix operator mathematical systems.

SAM76 language was designed to;

be very pure syntactically and semantically
require a minimum of user keyboarding to achieve powerful results
fit in a very small computer system
permit editing, testing, and executing modules interactively
not prevent the user from doing strange things with the syntax of the language yielding, however, predictable results.

Macro generators provide one of the keys to understanding the principles behind the development of the SAM76 language. A user will define a macro (a code word that can be defined by the user to invoke a specific set of instructions to perform a routine within the program) to execute a set of instructions, usually in either machine or assembly language, and insert the macro in the program. In this way, a user need only define a routine once and then when that particular operation, or string is required, the user can substitute the macro.

Characteristics of the SAM76 language

The SAM76 language follows a well defined syntax which is easy to learn and to read. It relies heavily, however, on a system of symbols to replace the pseudo English words of BASIC and Pascal.

The SAM76 interpreter also provides for a highly reactive and interactive language that can almost converse with the user from task to task. Consequently, the language has the capability of performing complex operations in program control, text editing and manipulation, gaming, simulation, and mathematics.

Because it has features similar to LISP, Forth and other list processors, SAM76 also has the capability of functioning as a query language, providing powerful human machine interaction that uses keyboard data from an interaction to modify and shape future responses. The language is also capable of growing by entension. Because, like LISP and Logo, there is almost no difference between procedures and data structures, procedures can be treated as data and be acted upon by other procedures, even procedures defined by different users. The new procedures that are mapped or created behave as if they were language primitives or inherent functions of the language. Like Logo, this means that new users can create their own separate vocabularies which can be saved and executed, adding to the language vocabulary and providing for individual customization.

Notation and Syntax

An expression may be characterised as being "active," that is to say its value string is subject to rescanning, "neutral" the value will not be rescanned or "protected" meaning "quoted" or immune from evaluation. Typically these are:

%active expression/ &neutral expression/ !protected string/

Like LISP, all commands and data objects in SAM76 are represented by lists, or strings of characters. However, in the latter language, syntax plays a vital role in identifying those characters which, because of their position in a given expression, have an additional meaning. The characters are called warning characters and represent the following concepts:

       %       start symbol for active expression
       &       start symbol for neutral expression
       !       start symbol for protected string
       /       end symbol for all types of expressions
       
       
       #       alternate start of expression
       :       end of active alternate expression
       ;       end of neutral alternate expression
       
       
       ,       argument separator symbol
       ( )     string protection pair
       < >     alternate protection pair
       @       protect or quote next single character
       `       ignore next single character
       [ ]     reserved as boundaries for special expressions
       
       
       Expressions may reach the scanner from various sources such as a
       keyboard  or  a  file  or a communications channel. This type of
       input  stream is commonly terminated by an activating character.
       Initially  this  activating character is set to be the "=" sign,
       although   it  may  be  changed  using  the  "change  activator"
       function.
       
       
       Other means of terminating the input stream includes an explicit
       character count, the encounter of one or more specified patterns
       of characters, or a user-specified timing function.
       
       
       When characters which are also used as warning characters are to
       be  part  of  the  data, they must be protected, either by being
       enclosed in one of the allowable protection pairs or preceded by
       the single character protection code.
       
       �         
       The SAM76 language                                <Page No.   5>
       ----------------------------------------------------------------
       
       
       
       A  legal SAM76 expression is a string bounded at its left end by
       a  start  symbol,  and  at  its right end by the appropriate end
       symbol. Elements of the expression are separated from each other
       by  the  argument  separator (,). The first argument is always a
       command,  or  the  name  of a user-defined string, expression or
       procedure.  Subsequent arguments (1, 2, 3, ... N) are treated as
       required  by the command or as macros which will be plugged into
       the proper places of the named user-defined string. For example:
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       	o  %ad,%mu,2,3/,%di,20,5//={10}
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~~
       
       
       The  foregoing  example consists of an expression which will add
       the  values  resulting  from the multiplication of 2 and 3, with
       the  division  of 20 by 5. Note that expressions are scanned and
       evaluated from left to right and inside out.
       
       
       It  is also possible to create user defined functions. First the
       user will define a "text" named "square" to be a procedure which
       will multiply some value "x" by "x":
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       	o  %dt,square,!%mu,x,x///={}
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~~
       
       
       Note  that  in  the foregoing step the multiplication expression
       has  been protected by the pair of warning characters ! .../ and
       the act of defining with the function "dt" simply creates a data
       object called "square" but returns no value.
       
       
       The  next  step is to convert the characters "x" into partitions
       (parameter  positions)  of  value  1  using the "partition text"
       command:
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)
       	o  %pt,square,x/={}
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       
       �         
       The SAM76 language                                <Page No.   6>
       ----------------------------------------------------------------
       
       
       
       If  we  now  examine  the  object named square with the function
       "view text" whose mnemonic is "vt" we will see:
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)
       	o  %vt,square/=
       	o  %mu,[1],[1]/
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       
       
       We  can  make  use  of  this new function to square numbers. For
       example:
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)
       	o  %square,5/={25}
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       
       
       Or, using the mnemonic "ad" for addition:
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)
       	o  %square,%ad,3,2//={25}
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       
       �         
       The SAM76 language                                <Page No.   7>
       ----------------------------------------------------------------
       
       
        ______________________________________________________________ 
       ||                                                            ||
       ||                    Descriptive examples                    ||
       ||                                                            ||
        ______________________________________________________________ 
       
       
       
       When  the  SAM76  language  is  initially  started the following
       expression is loaded:
       
       
               &os,%is//
       
       
       This  is  known  as  the  RESTART  expression and consists of an
       "input   string"   command  nested  inside  an  "output  string"
       expression.  In effect this says "Output that which results from
       evaluating   that  which  is  input".  When  all  evaluation  is
       completed   the  expression  is  reloaded  and  the  process  is
       repeated.  The  restart  expression  is  invisible  to the user.
       Initially,  the  requirement for user input is the result of the
       execution  by the scanner of the "is" command. The output of the
       material  entered  by  the user is dictated by the "os" command,
       for example:
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)
       	o  %ad,1,9/={10}
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       
       
       The  user  enters  "%ad,1,9/" followed by an "=" sign to signify
       end  of  input.  The  entered epression replaces the %is/ in the
       restart expression:
       
       
               &os,%ad,1,9//
       
       
       This results in
       
       
               &os,10/
       
       
       which is in turn evaluated to output the value 10.
       
       
       The  four  ways  in which user-defined functions or texts may be
       fetched or invoked are:
       
       
       %name, ... /            active value implied fetch
       &name, ... /            active value neutral implied fetch
       %ft,name, ... /         active value, explicit fetch text
       &ft,name, ... /         neutral value, explicit fetch.
       
       
       In  the  first  three modes shown above the value string will be
       rescanned  and  evaluated. The fourth expression will return the
       object called "name" as if it had been quoted.
       
       �         
       The SAM76 language                                <Page No.   8>
       ----------------------------------------------------------------
       
       
       
       The first example illustrates the use of partitions to translate
       text  by  parametrizing  the  positions of the different English
       words by replacing them with an internal marker which identifies
       the position value. Strings that remain between these partitions
       are referred to as "elements."
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)
       	o  %dt,text,
       	o  the dog and the cat and the horse/={}
       	o  %pt,text,the,dog,and,cat,horse/={
       	o  }
       	o  %text,le,chien,et,chat,cheval/={
       	o  le chien et le chat et le cheval}
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       
       
       The  first  line  of  the example shows the definition of a text
       named  "text"  to  contain  the  phrase "the dog ... horse." The
       second  line  uses the "partition text" function to convert each
       of the words in "text" to partitions whose value will correspond
       to  the  position  in  the  "pt"  expression  of the words being
       matched.
       
       
       The  last  line  in  the  example  shows  the  invocation of the
       partitioned  text  using a list of French words as the source of
       data   to   fill  the  partitions  with  words  whose  positions
       correspond to the value of the partitions.
       
       
       Use of the "view text" function to examine the text "text" would
       reveal the partitions in the following manner:
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)
       	o  %vt,text/=
       	o  [1] [2] [3] [1] [4] [3] [1] [5]
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       
       
       Notice  that  this  is  not  an "intelligent" translation of the
       English  into  the French because any words can be inserted into
       the  partition  frames  for  the conversion process to work. All
       that  is  happening  here is that in input string is partitioned
       and  a  new string, corresponding to the existing partitions, is
       imposed upon the script.
       
       
       It  is  evident from the examples that syntax plays a vital role
       in  the  SAM76  language,  defining  the  sequence of operations
       within each string. Use of mnemonics reduces the overhead which,
       unlike  BASIC, allows complicated programs to be written without
       an  overabundance  of  code.  For  example, the followin example
       illustrates  the construction of a password checking system with
       an  automatic exit if either an incorrect password is intered or
       there is no action after a given time.
       
       �         
       The SAM76 language                                <Page No.   9>
       ----------------------------------------------------------------
       
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)
       	o  %dt,password,!%ca,%xc,0D//%os,
       	o  Enter password followed by "return" ?- /%iw,100/`
       	o  %dt,x,&is//%ig,%crd,x/,,!%gotinput//,`
       	o  !%os, TIME OUT/%ex///////=
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       
       
       Let  us  now  read the first step, noting that bold face letters
       form   the   mnemonics   of  the  commands.  The  passage  below
       illustrates  the SAM76 stream of consciousness method of writing
       the language and is best understood if read aloud.
       
       
       "Define  a Text named 'password' to be a procedure (indicated by
       the  first  exclamation  point)  ...  this  procedure will first
       Change the Activator to be that character which results from the
       'X'  base  to  Character conversion of HEX 0D (namely a carriage
       return code) ...
       
       
       next this procedure will Output the String: '(CR LF codes)
       Enter password ... ?- ' ...
       
       
       following  this,  the  procedure  will set the Input Wait timing
       function  for  100 time units ... the ignore symbol that follows
       is  to  permit  the use of a (CR LF code) here that is not to be
       evaluated ...
       
       
       the  procedure  will  then  Define  a  Text named 'x' which will
       contain any material that is entered from the keyboard ... input
       termination will then be either the return code specified by the
       initial  'change activator' command, or with time out after time
       set by the 'input wait' function ...
       
       
       subsequent  to  input or time out, the procedure tests to see If
       Greater  the number of Characters to the Right of the Divider in
       'x'  than  zero  (indicated  by  the null string between the two
       adjacent commas) ... if 'x' contains one or more characters then
       control  is transferred to a procedure 'gotinput' to be defined,
       else  we  will  Output  the  String  ' TIME OUT' and EXit to the
       operating system."
       
       
       However, if the procedure finds that there are characters in the
       set (x), then the following routine applies:
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)
       	o  %dt,gotinput,!%ii,&ft,x/,SAM76,!%os,
       	o  You got it right/%ri//,!%os,
       	o  Wrong - Try again/%password//////=
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       
       
       Translated, this second procedure reads:
       
       �         
       The SAM76 language                                <Page No.  10>
       ----------------------------------------------------------------
       
       
       
       "Define a Text named "gotinput" to be a procedure that will test
       to  determine  if  the content of 'x' is Identical to the string
       'SAM76'  ...  if  it is identical then Output the String '(CR LF
       code)You  got  it  right' and Return the user to the Initialized
       condition  ...  if  not  identical then Output the String 'CR LF
       code)Wrong  ...'  and  invoke  the  procedure  named  'password'
       again."
       
       �         
       The SAM76 language                                <Page No.  11>
       ----------------------------------------------------------------
       
       
       
       The  next  example  illustrates  the  use of the multi-partition
       capability of the SAM76 language. A multi-partition is a special
       type  of  partition  which  is filled by all arguments of a list
       whose positions, counting from the left, are equal to or greater
       than  the  value of the multi-partition. Each term from the list
       which  is  placed  in  the  multi-partition  is  preceded by the
       "argument separator" character.
       
       
       This  permits the processing of lists of undefined and arbitrary
       lengths.  The  elements  of  the  list  may  be text strings, or
       procedures.   The   multi-partition   also   provides  tools  to
       manipulate matrices and other types of arrays.
       
       
       The procedure which is defined below is designed to tabulate the
       names of the files on a disk giving their size.
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)
       	o  %dt,tabulate,!%loop%lf,@,////=
       	o  %dt,loop,!%ii,q1,,,!%os,
       	o  q1 - %qfs,q1//%loopmp2//////=
       	o  %pt,loop,q1/%mt,loop,,mp2/=
       	o  %vt,loop/=
       	o  %ii,[1],,,!%os,
       	o  [1] - %qfs,[1]//%loop[#2]///
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       
       
       A  procedure  named  "tabulate" is defined as an invocation to a
       procedure named "loop" ... arguments to this procedure come from
       the evaluation of the "lf" function which returns a list of file
       names ... each file name is preceded by a comma.
       
       
       A  procedure  named  "loop"  is  defined  which  through a dummy
       argument  q1, to be parametrized, tests for the end of the list.
       If  the  end of the list is not reached, then an "output string"
       function  is  executed  with  the  name of the current file name
       being  plugged  into  the two other q1 positions. The first will
       merely display the file name, and the second is an argument to a
       "query  file  size"  function.  At  the  completion  of the "os"
       function  the procedure "loop" is reinvoked with arguments being
       the second term of this list to its end.
       
       �         
       The SAM76 language                                <Page No.  12>
       ----------------------------------------------------------------
       
       
       
       The  "partition text" and "multi-partition text" expressions are
       used to convert the dummy entries in loop to appropriate values.
       
       
       In order to execute the foregoing program we merely enter:
       
               %tabulate/=
       
       and the tabulation will follow.
       
       �         
       The SAM76 language                                <Page No.  13>
       ----------------------------------------------------------------
       
       
       
       Two  examples  of  the  use of SAM76 in the solution of problems
       using recursion are shown below.
       
       
       The  first  procedure  calculates  the  integer factorial of any
       number. The procedure name is 'FAC' and a View Text of FAC would
       display:
       
       
       %ii,[1],1,1,!%mu,[1],%FAC,%su,[1],1/////
       
       
       For example the factorial of 30 would be determined thus:
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)
       	o  %FAC,30/={265252859812191058636308480000000}
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       
       
       The  second  example  illustrates  a  recursive way to solve the
       problem of the towers of Hanoi, a favorite with afficionadoes of
       this type of language; Viewing Text named "HANOI" we see:
       
       
       %ii,[1],0,,!%HANOI,%su,[1],1/,[2],[4],[3]/!
       Move Ring [1] from [2] to [3]/%HANOI,%su,[1],1/,[4],[3],[2]///
       
       
       Assuming  three  towers  named  "here", "middle" and "there" the
       moves  required  to  move  4  rings from "here" to "there" using
       "middle" as a way station would be determined as follows:
       
       	o17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)
       	o  %HANOI,4,here,there,middle/={
       	o  Move Ring 1 from here to middle
       	o  Move Ring 2 from here to there
       	o  Move Ring 1 from middle to there
       	o  Move Ring 3 from here to middle
       	o  Move Ring 1 from there to here
       	o  Move Ring 2 from there to middle
       	o  Move Ring 1 from here to middle
       	o  Move Ring 4 from here to there
       	o  Move Ring 1 from middle to there
       	o  Move Ring 2 from middle to here
       	o  Move Ring 1 from there to here
       	o  Move Ring 3 from middle to there
       	o  Move Ring 1 from here to middle
       	o  Move Ring 2 from here to there
       	o  Move Ring 1 from middle to there}
       	o
       	17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)17:11, 2 August 2007 (UTC)~
       
       
       These   examples   indicate   that  the  SAM76  language  offers
       interesting  possibilities  to programmers because its structure
       resembles  the  structure  of logical or procedural thought very
       closely, and its system of ready-to-hand mnemonics can eliminate
       much of the coding overhead associated with BASIC.
       
       �         
       The SAM76 language                                <Page No.  14>
       ----------------------------------------------------------------
       
       
       
       Currently, the SAM76 language enjoys implementation on most CP/M
       systems including the Apple II and IIe, as well as under MSX-DOS
       and on the very much larger DEC System 10.
       
       �         
       The SAM76 language                                <Page No.  15>
       ----------------------------------------------------------------
       
       
        ______________________________________________________________ 
       ||                                                            ||
       ||                     Resident Functions                     ||
       ||                                                            ||
        ______________________________________________________________ 
       
       
       
       All resident functions consist of not less than two and not more
       than  three  alphabetic  characters.  In  general  the  mnemonic
       assigned  consists,  in the case of single word commands, of the
       first  two  letters of the command. In the case of multiple word
       commands,  the  mnemonic consists of the first letter of each of
       the several words which form the command.
       
       
       Each  resident  function in a standard system has assigned to it
       an  abitrary  serial  number.  This  number is used to precisely
       identify  the formal definition of each function. This method of
       correlation serves several purposes, namely, ...
       
       
       (1)  An  implementation  of the SAM76 language may be defined in
       terms of the available function numbers and initial selection of
       function  mnemonics.  The  user  can  then safely assume correct
       operation  of functions if the implementation definition matches
       the one being used.
       
       
       (2)  A more important use for this identification scheme relates
       to   the  international  usage  of  SAM76.  Commands  and  their
       associated mnemonics may be clear in one user's language such as
       "English,"  but  be  obscure in some other language as "French."
       The  provision  of a function in the SAM76 language that changes
       the  mnemonics  in the resident function tables permits the most
       effective use of command words in a variety of languages.
       
       
       (3)  Portability  of  user scripts across international language
       boundaries  is simplified since it is not necessary to translate
       the  command  arguments  in  the  programs  from one language to
       another.  Instead  the  state  of  the  machine  may  be readily
       switched from one mode to the other at any time.
       
       
       The  list  of  functions  in  the following table is arranged by
       functional   category.   The  first  argument  is  the  function
       mnemonic.  Subsequent  arguments are identified by abbreviations
       as  defined  below.  The active form for each function is shown.
       The  neutral  form  of  a  function is shown only in those cases
       where a different action is performed from its active form. This
       is the case only for those functions which have a null value.
       
       
       Note that the functions listed in this description form only the
       minimal  set of a standard implementation of the SAM76 language.
       Some  of  these  functions  have  sub functions; other functions
       exist in specialized system implementations.
       
       �         
       The SAM76 language                                <Page No.  16>
       ----------------------------------------------------------------
       
       
        ______________________________________________________________ 
       ||                                                            ||
       ||        ABBREVIATIONS USED IN THE LIST OF FUNCTIONS         ||
       ||                                                            ||
        ______________________________________________________________ 
       
       
       
       
       %function,arguments,......./            Active expression
       &function,arguments,........../         Neutral expression
       
       
       x,x1,...        "x" base (binary, octal, hex) numbers
       d,d1,...        Decimal base numbers
       n,n1,...        "n" base (arithmetic) numbers
       s0              Prefixing string (as in lists)
       s,s1,...        character strings
       f               file name
       t               text name
       vz              default value
       v-,v+,v0        conditional value
       vt,vf           true/false value
       sub             indicates sub-functions - using
                       "lf,s0" as subfunction gives list.
       
       
       A  hyphen  following  the  function  number  signifies that this
       function   has   been  added  to  th  list  since  the  original
       publication  in  the "Mc Graw Hill Personal Computer Programming
       Encyclopedia" in 1985.
       
       
       TEXT FUNCTIONS
       
       
               TEXT MANIPULATION
       
       103     %dt,t,s,d1,d2/          ;Define Text
       104     %et,t1,t2,...,t/        ;Erase Text
       105     %lt,s0/                 ;List Text
       106     %ft,t,s1,s2,...,s/      ;Fetch Text
       114     %ht,t/                  ;Hide Text
       118     %vt,t1,t1,...,t/        ;View Texts
       132     %ct,t1,t2,t3,...t/      ;Combine Texts
       206     %ea/                    ;Erase All
       
       
               TEXT DIVISION
       
       137     %fc,t,vz/               ;Fetch Character
       138     %fdc,t,d,vz/            ;Fetch "D" Characters
       139     %fde,t,d,vz/            ;Fetch "D" Elements
       140     %fdm,t,d,s,vz/          ;Fetch "D" Matches
       141     %fe,t,vz/               ;Fetch Element
       142     %ff,t,d,vz/             ;Fetch Field
       143     %fl,t,s,vz/             ;Fetch Left match
       144     %fr,t,s,vz/             ;Fetch Right match
       145     %fp,t,x1,x2,...,x/      ;Fetch Partition
       146     %md,t,d/                ;Move Divider to pos. "d"
               &md,t,d/                ;Move Divider "d" positions     �         
       The SAM76 language                                <Page No.  17>
       ----------------------------------------------------------------
       
       
       147     %crd,t/                 ;Characters right of divider
       148     %cld,t/                 ;Characters Left of Divider
       197     %qld,t/                 ;Query Left of Divider
       198     %qrd,t/                 ;Query Right of Divider
       207     %ed,t,d1,d2,vz/         ;Extract "D" characters
       210     %ftb,t,s,vz/            ;Fetch To Break character
       211     %fts,t,s,vz/            ;Fetch To Span character
       
       
       
       STRING FUNCTIONS
       
       150     %hm,t,s/                ;How many Matches
       160     %ai,s0,s1,s2,...,s/     ;Alphabetic Insertion
       161     %as,s0,s1,s2,...,s/     ;Alphabetic Sort
       162     %ps,d,s1,s2/            ;Pad String
       163     %rs,s/                  ;Reverse String
       164     %ds,d,s/                ;Duplicate String
       168     %tr,t,s/                ;Trim
       209     %nu,s1,s2,...,s/        ;Null
       212     %hc,s/                  ;How many Characters
       214     %lw,s0,s1,s2,...,s/     ;List Where
       215     %ra,d,s1,s2,s3,...,s/   ;Return Argument
       247     %rj,d,s1/               ;Return Justified lines
       248     %rp,c,d,s1/             ;Return Padded lines
       
       
       
       BRANCH FUNCTIONS
       
       111     %ni,vt,vf/              ;Neutral Implied
       126     %yt,t,s,vt,vf/          ;Ys There
       127     %tb,t,vt,vf/            ;Text Branch
       135     %ii,s1,s2,vt,vf,.../    ;If Identical
       136     %ig,d1,d2,vt,vf,.../    ;If Greater
       159     %ab,s1,s2,vt,vf/        ;Alphabetic Branch
       226     %fb,f,vt,vf/            ;File Branch
       900     %gel,d1,d2,v+,v0,v-/    ;Greater Equal or Less
       
       
       
       MATHEMATICAL FUNCTIONS
       
       
               ARITHMETIC
       
       128     %ad,n1,n2,n3,...,n/     ;Add
       129     %su,n1,n2,...,n/        ;Subtract
       130     %di,n1,n2,vz/           ;Divide
       131     %mu,n1,n2/              ;Multiply
       
               LOGICAL
       
       186     %or,x1,x2/              ;Or the bits
       187     %and,x1,x2/             ;And the bits
       188     %not,x/                 ;Not (complement) the bits
       189     %rot,d,x/               ;Rotate the bits
       190     %sh,d,x/                ;Shift the bits�         
       The SAM76 language                                <Page No.  18>
       ----------------------------------------------------------------
       
       
       
       
       
       PARTITION FUNCTIONS
       
       107     %pt,t,s1,s2,...,s/      ;Partition Text
       108     %pc,d/                  ;Partition Character
       109     %mt,t,s1,s2,...,s/      ;Multi-part Text
       110     %mc,d/                  ;Multi-part Character
       149     %hp,t,d/                ;How many Partitions
       151     %ep,t,p1,p2,...,p/      ;Erase Partitions
       167     %qp,t/                  ;Query Partition
       
       
       
       I/O FUNCTIONS
       
       101     %os,s/                  ;Output String
       102     %is/                    ;Input String
       115     %ic/                    ;Input Character
       116     %id,d/                  ;Input "D" Characters
       117     %im,s1,s2,...,s/        ;Input to Match
       213     %iw,n/                  ;Input Wait
       241     %lic,s0/                ;List Input Channels
       242     %loc,s0/                ;List Output Channels
       245     %sic,sym/               ;Select Input Channel
       246     %soc,sym/               ;Select Output Channel
       264     %qio/                   ;Query I/O assignments
       265     %sio,iobyte/            ;Set I/O byte
       
       
       
       STORAGE FUNCTIONS
       
       216     %lf,s0/                 ;List Files
       217     %qfs,filename/          ;Query File Size
       219     %qfe/                   ;Query File Extension
       220     %bf,f/                  ;Bring File
       221     %sfe,extension/         ;Set File Extension
       222     %sf,f/                  ;Store File
       223     %sdu,dir/               ;Select Directory Unit
       224     %ef,f/                  ;Erase File
       225     %qdu/                   ;Query Directory Unit
       233     %dif,filename/          ;Designate Input Filename
       234     %dof,filename/          ;Designate Output Filename
       235     %rfr/                   ;Read File Record
       236     %wfr,s/                 ;Write File Record
       243     %rf,filename/           ;Read File
       244     %wf,filename,s/         ;Write File
       
       
       
       RANDOM NUMBER
       
       252     %rn,n/                  ;Random Number
       253     %srn,n/                 ;Seed Random Number
       
       �         
       The SAM76 language                                <Page No.  19>
       ----------------------------------------------------------------
       
       
       
       CONVERSION
       
       170     %xc,x1,x2,...,x/        ;X to Character
       171     %cx,s0,s/               ;Character to X
       172     %xd,x/                  ;X to Decimal
       173     %dx,d/                  ;Decimal to X
       
       
       
       GRAPHICS
       
       174     %pl,sub,s1,...,s/       ;Plot
       175     %wi,xn1,yn1/            ;Write Initialize
       176     %wx/                    ;Write X displacement
       177     %wy/                    ;Write Y displacement
       178     %wr/                    ;Width Right
       179     %wl/                    ;Width Left
       180     %ws,xn1,yn1,...,xn,yn/  ;Write Straight lines
       
       
       
       SOFTWARE "Z" COUNTERS
       
       182     %zd,r,v-,v0,v+/         ;"Z" reg. Decrement and branch
       183     %zi,r,v-,v0,v+/         ;"Z" reg. Increment and branch
       184     %zq,r/                  ;"Z" reg. Query
       185     %zs,r,n/                ;"Z" reg. Set
       
       
       
       TRACE MODES
       
       124     %tma/                   ;Trace Mode All deactivated
               &tma/                   ;Trace Mode All activated
       125     %tm,d/                  ;Trace Mode activated
               &tm/                    ;Trace Mode deactivated
       
       
       
       CONTROL FUNCTIONS
       
       113     %ca,s/                  ;Change Activator
       133     %cnb,d/                 ;Change Number Base
       134     %qnb/                   ;Query Number Base
       157     %sfd,fun,dev/           ;Specify Function Device
       158     %sar/                   ;Set Auto Return on line feed
       169     %ut,cc/                 ;User Trap
       191     %cll,d/                 ;Change Line Length
       192     %qll/                   ;Query Line Length
       193     %cin,t1,d1,...,t,d/     ;Change Id Number
       194     %qin/                   ;Query Id Number
       195     %cfc,d1,s/              ;Change Fill Character schema
       196     %qfc,s0/                ;Query Fill Character schema
       199     %sem,dev/               ;Set "Echoplex" Mode
       200     %cxb,d/                 ;Change X base
       201     %qxb/                   ;Query X base
       202     %qof/                   ;Query Overflow Functions
       203     %cro,s1/                ;Change Rub Out character schema�         
       The SAM76 language                                <Page No.  20>
       ----------------------------------------------------------------
       
       
       204     %qro/                   ;Query Rub Out character schema
       205     %qta/                   ;Query Text Area
       227     %qcs/                   ;Query Command String
       237     %@t/                    ;wh@ is processor Title
       238     %@f,s0/                 ;wh@ are Functions
       239     %@n/                    ;wh@ is processor ver. Number
       240     %@cn,current,new/       ;Change Name of function
       250     %cwc,s1/                ;Change Warning Characters
       251     %qwc/                   ;Query Warning Characters
       261     %cws,d/                 ;Change Work Space
       262     %qws/                   ;Query Work Space
       266     %cpc,x1,t1,...,tn/      ;Change Protection Class
       267     %qpc,s0,t1,t2,...,t/    ;Query Protection Class
       
       
       
       MISC. FUNCTIONS
       
       112     %ex,f/                  ;Exit
       155     %xll,s0/                ;Xamine Label List
       156     %xal,label,x/           ;Xamine Address of Label
       165     %rr,s1/                 ;Return to Restart
       166     %ri/                    ;Restart Initialized
       228     %lff,s0/                ;List File Functions
       231     %sw,s1,s2,s3,...,s/     ;Switches
       232     %sy,s1,s2,...,s/        ;System Functions
       257     %ti,s0/                 ;Time
       258     %sti,hh,mm,ss/          ;Set Time
       259     %da,s0/                 ;Date
       260     %sda,da,mo,yr/          ;Set Date
       268     %nud,func,arguments/    ;Null Display mode
       289 -   %rgc,d/                 ;Read Game Controller
       290 -   %ipb,d,t,f/             ;If Push Button
       291 -   %san,d,x/               ;Set Annunciator
       301 -   %dow/                   ;Day Of Week
       303 -   %bsr,subfun,arg2,..../  ;BSR controller functions
       304 -   %lef,s0/                ;List Extended Functions
       
       
       EXPERIMENTATION FUNCTIONS
       
       119     %xr,x/                  ;eXamine Register
       120     %xw,x1,x2/              ;eXperimental Write in reg.
       121     %xrp,x/                 ;eXamine Register Pair
       122     %xwp,x1,x2/             ;eXperimental Write in reg. Pair
       123     %xj,x/                  ;eXperimental Jump
       254     %xqs,s0/                ;X Query work Space
       255     %xi,port/               ;eXperimental Input
       256     %xo,x,port/             ;eXperimental Output
       269     %xrs,unit,trk,sec,s0/   ;X Read Sector
       270     %xws,unit,trk,sec,X/    ;X Write Sector
       271     %xu,sub,arguments/      ;Xperimental User
       272     %xqf,s/                 ;eXperimental Query Function
       273     %xcf,s,x/               ;eXperimental Change Function
       
       �         
       The SAM76 language                                <Page No.  21>
       ----------------------------------------------------------------
       
       
       
       SYSTEM OR MACHINE DEPENDENT FUNCTIONS
       
       274 -   %trs,subf,a1,a2,../     ;TRS 80 Model 1
       288 -   %son,subf,a1,a2,../     ;SONY SMC70
       302 -   %pcc,subf,a1,a2,../     ;PC Compatibles
       305 -   %msx,subf,a1,a2,../     ;MSX machines
       
       
       GRAPHICS PRINTER FUNCTIONS
       
       287 -   %eps,subf,a1,a2,../     ;EPSON MX, FX &c.
       295 -   %ips,subf,a1,a2,../     ;Itoh Print System
       
       �         
       The SAM76 language                                <Page No.  22>
       ----------------------------------------------------------------
       
       
        ______________________________________________________________ 
       ||                                                            ||
       ||                         References                         ||
       ||                                                            ||
        ______________________________________________________________ 
       
       
       
       1.      Strachey,  C.  -  "A  general  purpose  macrogenerator",
       Computer Journal, Vol. 8, No. 3, Oct. 1965 p. 225;
       
       
       2.      Hall,   Andrew   D.  -  "The  M6  macroprocessor",  Bell
       Telephone Labs; Computer Science Report No. 2; 1971;
       
       
       3.      Roichel,  Ancelme  &  al. "SAM76 Language System", DECUS
       (Digital  Equipment  User's  Group) library, Maynard, Mass., No.
       10-342, 1982.
       
       
       4.      Kagan,  Claude  A. R. - "A string language Processor for
       small machines", Proceedings of the ACM SIGPLAN Symposium on the
       Pedagogical  Applications  of  small  Computers,  University  of
       Kansas, Lawrence, Kansas , Nov 18, 1971.
       
       
       5.      Kagan, Claude A. R., "The SAM76 Language", IEEE Computer
       Society Repository, R76-301, August 1976.
       
       
       6.      Roichel, Ancelme, and Nicholas, Karl, "SAM76 - The First
       Language  Manual", SAM76 Inc., Pennington, N.J., Second Edition,
       1978.
       
       
       7.      Various  -  "SAM76 Language - descriptions and updates",
       Dr. Dobb's Jounal, Volume 3 for the year 1977.
       
       
       8.      Kagan,  Claude  A.  R.  and  Nicholas,  Karl, "The SAM76
       Language",   in   "Mc   Graw  Hill  Personal  Computer  Language
       Encyclopedia", NYC, 1985.
       
       
       9.      Kagan, Claude A. R. and Nicholas, Karl, "Exotic Language
       of  the Month - The SAM76 language", Computer Language Magazine,
       November 1985.
       
       
       10.     Kagan,  Claude  A.  R.  and  Nicholas,  Karl, "SAM76 and
       TRAC", in Computer Language, January 1986, page 10.
       
       �         
       The SAM76 language                                <Page No.  23>
       ----------------------------------------------------------------
       
       
        ______________________________________________________________ 
       ||                                                            ||
       ||                      ACKNOWLEDGEMENTS                      ||
       ||                                                            ||
        ______________________________________________________________ 
       
       
       
       
       
       
       
       
       
       The   following  people  contributed  in  various  ways  to  the
       development of the SAM76 language and its implementations: Roger
       Amidon,   Neil  Colvin,  Carl  Galletti,  Barry  Lubowsky,  Karl
       Nicholas,  L.  G.  Schear. Among the many others who contributed
       are  the following members of a former (1967-1971) group of high
       school  students  in New Jersey known as the R.E.S.I.S.T.O.R.S.:
       Chuck Ehrlich, J. N. B. King, Gnat Kuhn, Barry Klein, Bob Evans,
       David   Theriault,   John   Levine,   Gifford   Marzoni,   Peter
       Eichenberger, Jordan Young, Johnny Gorman, and Joseph Tulloch.
       
       
       Further  credit should be given to the following who assisted in
       many  ways in promoting and implementing the SAM76 language on a
       variety  of machines: Larry Stein of PRODIGY computers of N. J.,
       Mark  Wolinsky  -  Jim  and Dave Hair of Floppy Disk Services of
       Princeton, N. J., Dr. Al Katz at Trenton State College of N. J.,
       Hank Beechold also of Trenton State College who was instrumental
       in polishing up the material for the Mc Graw Hill publication.
       
       
       In  addition  thanks to the numerous "pioneers" who acquired the
       SAM76  language  and  who  through  their comments and feed back
       helped to support continuing effort for the last ten years.
       
       
       
       
                                       Claude A. R. Kagan - 1986

</nowiki>

Weirdo Bug

Code	Display
[[England national football team\|England]] [[Image:Flag of England (bordered).svg\|18px]]	England
[[England national football team\|England]] [[Image:Flag of England (bordered).svg\|19px]]	England
[[England national football team\|England]] [[Image:Flag of England (bordered).svg\|20px]]	England
[[England national football team\|England]] [[Image:Flag of England (bordered).svg\|21px]]	England
[[England national football team\|England]] [[Image:Flag of England (bordered).svg\|22px]]	England

UEFA Cup

History

The first incarnation of the UEFA cup was the Inter-Cities Fairs Cup was the brainchild of Ernst Thommen from Switzerland, Italy’s Ottorino Barrasi (both of whom became future vice-presidents of FIFA and Sir Stanley Rous, the future president of FIFA.

The competition lasted from 1955 to 1958, was a tournament open to cities that had hosted trade fairs, and not necessarily clubs - cities with more than one club sent representative teams (e.g. London).

The cities that participated in the initial tournament were Barcelona, Basle, Birmingham, Copenhagen, Frankfurt, Lausanne, Leipzig, London, Milan and Zagreb. This tournament was only supposed to last for two years but it ended up lasting for three. In which 23 games were played. The winner was Barcelona, who only fielded players from FC Barcelona beat the London XI side 8-2 on aggregate in the final.

A second tournament took place between 1958 and 1960, this tournament the organisers altered the format, making it club, as well as city teams that could enter, but the teams still had to come from cities the hold trade fairs, and changing the competition to a knockout with the sixteen teams that entered, it was also won by Barcelona. The third tournament was held over the course of the 1960-61 season, and all subsequent tournaments have been held on a yearly basis. In 1962 the number of entrants had gone up to 32, and again in 1967 to 48, 60 in 1968. And for the 1969-70 tournaments there were 64 teams starting. Today there are more than 100.

As time progressed, the competition saw more clubs and fewer representative sides enter, so that by the mid-1960s, it was exclusively for clubs, who usually qualified by virtue of a high finish in their domestic league. However, a rule that only one club per city could enter was applied. In the early days of the tournament, the southern European clubs dominated, notably Barcelona and Valencia, winning the competition five times between them. In 1968 Leeds won the competition, and were the first northern European club to do so.

The competition completely dropped its link with the trade fairs and the organisation responsibilities were handed over to UEFA, as they were the only organisation to have good enough administration and knowledge of the sport to run such a competition. UEFA Cup in 1971, with Tottenham Hotspur F.C being the first winner of the UEFA Cup. However, the 'one club per city' rule was only rescinded in 1975; Everton had finished fourth in the English league and could thus qualify, but were barred from entry because Liverpool had also qualified by coming second. Everton appealed, saying the rule was an unfair anachronism, and UEFA agreed to overturn it.

The competition was traditionally open to the runners-up of domestic leagues, but in 1999, the competition was merged with the Cup Winners' Cup. Since then the winners of domestic cup competitions have also entered the UEFA Cup. Also clubs that were eliminated in the third round of the UEFA Champions League and the eight third placed teams at the end of the group phase could go and compete in the UEFA Cup. Also admitted to the competition are three Fair Play representatives, three UEFA Intertoto Cup ‘winners’ and winners of some selected domestic league cup competitions.

The winners keep the trophy for a year, and after handing it back, can keep a four fifths size replica permanently. The regulations also states that the original trophy is handed to any club that wins the UEFA Cup three times in a row, or five times overall though, this has not happened, yet.

2010 FIFA World Cup

Venues

In 2005, the organisers released a provisional list of 13 venues to be used for the World Cup, to be eventually narrowed down to ten: Bloemfontein, Cape Town, Durban, Johannesburg (two), Kimberley, Nelspruit, Orkney, Polokwane, Port Elizabeth, Pretoria (two), and Rustenburg.

On 17 March, 2006, FIFA officially announced the final list of venues:

City	Stadium	Capacity
Bloemfontein (Mangaung)	Free State Stadium	40,000
Cape Town	African Renaissance Stadium (to be built)	68,000
Durban	King Senzangakhona Stadium (to be built)	60,000
Johannesburg	Soccer City	94,700
Johannesburg	Ellis Park Stadium	60,000
Nelspruit	Mbombela Stadium (to be built)	40,000
Polokwane	Peter Mokaba Stadium	40,000
Port Elizabeth	Nelson Mandela Bay Stadium (to be built)	50,000
Pretoria (Tshwane)	Loftus Versfeld Stadium	52,000
Rustenburg	Royal Bafokeng Stadium	40,000

2006 FIFA World Cup

Seeding

To calculate the seeding for the 2006 FIFA World Cup, FIFA used the FIFA World Rankings current and past standings) in combination with the previous world cup performances of national teams, to determine their seeds for the World Cup^[1]. It uses the points obtained from the 1998 FIFA World Cup and the 2002 FIFA World Cup averaged in a 1:2 ratio respectively, added to the average amount of points that each team has at three given dates (at ratio 1:1:1), December 2003, December 2004, and November 2005. This generates a view to how well the teams have performed over the last ten years (since the rankings in 2003 include results from eight years previous to that) with a specific focus on how the teams have performed in the FIFA World Cup on previous occasions. Obviously if a team did not qualify for the previous two World Cups, their final total will be significantly less, as is the reason the Czech Republic are ranked so low on the seedings, despite being only 6th, 4th, and 2nd in the world on the rankings at the given dates.

Seed	Country	1. FIFA World Cup Finals					2. FIFA World Rankings							Total Points
		France '98 (33.3%)		Korea Japan '02 (66.7%)		Avg. Points	Dec '03 (33.3%)		Dec '04 (33.3%)		Nov '05 (33.3%)		Avg. Points
		Rk	Pt.	Rk	Pt.	Avg. Points	Rk	Pt.	Rk	Pt.	Rk	Pt.	Avg. Points
1	Brazil	2	31	1	32	31.7	1	32	1	32	1	32	32.0	64
2	England	9	24	6	27	26.0	8	25	8	25	9	24	24.7	51
3	Spain	17	9	5	28	21.7	3	30	5	28	6	27	28.3	50
4	Germany	7	26	2	31	29.3	12	22	19	19	16	19	20.0	49
5	Mexico	13	20	11	22	21.3	7	26	7	26	7	26	26.0	47
6	France	1	32	28	8	16.0	2	31	2	31	5	28	30.0	46
7	Argentina	6	27	18	9	15.0	5	28	3	30	4	29	29.0	44
8	Italy	5	28	15	18	21.3	10	24	10	23	12	22	23.0	44
9	United States	32	8	8	25	19.3	11	23	11	22	8	25	23.3	43
10	Netherlands	4	29	-	0	9.7	4	29	6	27	3	30	28.7	38
11	South Korea	30	8	4	29	22.0	22	16	22	17	29	13	15.3	37
12	Japan	31	8	9	24	18.7	29	12	17	20	15	20	17.3	36
13	Sweden	-	0	13	20	13.3	19	19	13	21	14	21	20.3	34
14	Croatia	3	30	23	9	16.0	20	18	23	16	20	17	17.0	33
15	Paraguay	14	19	16	17	17.7	22	17	30	12	30	12	13.7	31
16	Czech Republic	-	0	-	0	0.0	6	27	4	29	2	31	29.0	29
17	Portugal	-	0	21	9	6.0	17	21	9	24	10	23	22.7	29
18	Costa Rica	-	0	19	9	6.0	17	20	27	14	21	16	16.7	23
19	Saudi Arabia	28	8	32	8	8.0	26	14	28	13	32	11	12.7	21
20	Poland	-	0	25	8	5.3	25	15	25	15	23	15	15.0	20
21	Iran	20	9	-	0	3.0	28	13	20	18	19	18	16.3	19
22	Tunisia	26	8	29	8	8.0	45	8	35	11	28	14	11.0	19
23	{{subst:ecUf}}	-	0	24	9	6.0	37	11	39	10	37	9	10.0	16
24	Serbia and Montenegro	10	23	-	0	7.7	41	10	46	8	47	6	8.0	16
25	Switzerland	-	0	-	0	0.0	44	9	51	7	36	10	8.7	9
26	Ukraine	-	0	-	0	0.0	60	7	57	6	40	8	7.0	7
27	Ivory Coast	-	0	-	0	0.0	70	5	40	9	41	7	7.0	7
28	Australia	-	0	-	0	0.0	82	3	58	5	49	5	4.3	4
29	Trinidad and Tobago	-	0	-	0	0.0	70	6	63	4	51	3	4.3	4
30	Ghana	-	0	-	0	0.0	78	4	77	2	50	4	3.3	3
31	Angola	-	0	-	0	0.0	83	2	72	3	62	1	2.0	2
32	Togo	-	0	-	0	0.0	94	1	89	1	56	2	1.3	1

European Football Championship

History

Birth of the Competition

In 1956, the groundwork for a European national team competition was laid. Two years later, in 1958, the first European Nations Cup began. The original format of the competition saw the early rounds played in home and away matches between the countries on a knockout basis. This continued until the semi-finals, where the remainder of the competition was played in the host country, chosen from the four semi-finalists.

The French Football Federation’s Henri Delaunay came up with the idea of a European championship in 1927. Given the immense efforts that Delaunay had put into setting up a European national teams competition, UEFA deemed it appropriate that the inaugural competition be hosted by France. The trophy presented to the competition winner still bears his name.

The first final was held in Paris and saw the Soviet Union defeat Yugoslavia, after extra time, and be first to have their name engraved onto the trophy.

The 1964 competition was the first European Nations Cup to be affected by politics as it saw Greece refusing to play Albania as they were technically (though not officially) at war. The finals were hosted by Spain, and they saw the hosts beat the Soviet Union 2-1 in Madrid.

New Format introduced

The European Nations Cup changed its name to the UEFA European Football Championship for 1968 and also a new format was introduced. Eight groups of seeded teams played each other twice and the top side of each group proceeded to two-legged quarter finals. The semi-finals and final were played in the host country of Italy who won the competition after a 2-0 replay of the final, having drawn 1-1 in the first against Yugoslavia.

In the 1972 tournament, the same structure was retained, with Belgium being the host of the finals. Germany won the competition, beating the Soviet Union 2-0 in the final. The 1976 final round was hosted by Yugoslavia. In the final, Czechoslovakia squandered a two-goal lead before penalties were needed. When Uli Hoeness missed, it allowed Antonín Panenka to chip into the space vacated by Sepp Maier's anticipatory dive for a Czechoslovakian victory.

Another Change

In 1980 UEFA introduced a new format, which saw eight teams go to the finals instead of four, and then play each other in two groups of four teams; the winner of each group then proceeded to the final. Germany faced Belgium in the final, which they won 2-0 after two goals from Horst Hrubesch. However the newer format was not retained in 1984, and a different format was used, again employing group stages, but this time in place of only the quarter-finals. The top two teams from each of the two groups progressed to the semi-finals. The competition was held in France for the second time. The hosts won 2-0 in Paris against Spain with goals from Michel Platini and Bruno Bellone.

The 1988 competition was held in Germany, while the format from the 1984 competition was retained. Marco Van Basten led the Netherlands, scoring what was later voted the best goal ever in the competition ^[2].

Great Political Change

The 1992 competition was held in Sweden during a time of European political change, a united Germany was represented and as a result of the break up of the Soviet Union, a Commonwealth of Independent States of the former Soviet Union. Yugoslavia made it to the finals but were excluded as a result of hostilities in their country, Denmark replaced them. Surprisingly, the Danes went on to win the competition after a 2-0 victory over world champions Germany in the final.

With the break up of the Soviet Union all of the former Soviet bloc countries were required to enter separately. Now that there were more teams, a format that accommodated this was required. With 48 teams entering the competition, and after the enlargement of the World Cup which had more European sides qualifying for it than the European Championships themselves, 16 teams travelled to the finals in England. The teams were put into 4 groups , the winner and runner up of each group progressed to a new round of quarter-finals. The semi-finals and final remained the same. The Germans won in the final over underdogs Czech Republic with a golden goal.

The New Millenia

Belgium and the Netherlands became the first countries to jointly host the event in 2000. France won, again the final was decided by golden goal, David Trezeguet was the scorer. In 2004 the event was held in Portugal, with the silver goal rule being used for the first time. The rule saw Greece beat the Czech Republic in the semi-finals. Underdogs Greece went on to win the competition, when they had been put at pre-tournament odds of 100 to 1. The next tournament will be co-hosted by Switzerland and Austria in 2008.

Format

Qualifying

In order to qualify a team must be winners or runners-up in one the seven qualifying groups. After this a team proceeds to the finals round in the host country, although hosts qualify for the tournament automatically. The qualifying phase begins in the autumn after the preceding FIFA World Cup, almost two years before the finals.

The groups for qualification are drawn by a UEFA committee using seeding, seeded teams include reigning champions, and other teams on the basis of their performance in the preceding FIFA World Cup qualifying, and the last European Football Championship qualifying. To obtain an accurate view of the teams abilities, a ranking is produced, this is calculated by taking the total number of points won by a particular team, and dividing it by the number of games played, i.e., points per game, in the case of a team having hosted one of the two previous competitions, and therefore having qualified automatically, only the results from the single most recent qualifying competition are used. If two teams have equal points per game, the committee then bases their positions in the rankings on;

Coefficient from the matches played in its most recent qualifying competition.
Average goal difference.
Average number of goals scored.
Average number of away goals scored.
Drawing of lots.

Groups

The qualifying phase is played in a group format, the composition of the groups is determined through means of a draw of teams from pre-defined seeded bowls. The draw takes place after the preceding World Cup's qualifying competition. For the 2008 European Football Championship, the group qualifying phase consists of seven groups, one of eight teams, and the remainder of seven teams each.

The qualifying phase is done in groups, each a effectively a mini league, where the highest ranked team, after all the teams have played each other home and away, progresses to the finals tournament, as with most leagues, the points are dealt as three for a win, one for a draw, and none for a loss. In the eventuality of one or more teams having equal points after all matches have been played, the following criteria is used to distinguish the sides;

Higher number of points obtained in the group matches played among the teams in question.
Superior goal difference from the group matches played among the teams in question.
Higher number of goals scored in the group matches played among the teams in question.
Higher number of goals scored away from home in the group matches played among the teams in question.
Results of all group matches:
1. Superior goal difference
2. Higher number of goals scored
3. Higher number of goals scored away from home
4. Fair play conduct.
Drawing of lots.

Final Tournament

Sixteen teams progress to the finals tournament, for the 2008 tournament they will be the winners and runners up of the seven qualifying groups, and joint hosts Austria and Switzerland. These sixteen teams are divided equally into four groups, A, B, C and D, each consisting of four teams. The groups are drawn up by the UEFA administration, again using seeding. The seeded teams being the host nations, the reigning champions, subject to qualification, and those with the best points per game coefficients over the qualifying phase of the tournament and the previous World Cup qualifying. Other finalists will be assigned to groups by means of a draw, using coefficients as a basis.

The four aforementioned groups are again played in a league format, this time, a team plays its opponents once each, in the host nation, not home and away. The same scoring system is used (three points for a win, one point for a draw, no points for a defeat). A schedule for the group matches will be bran up, but the last two matches in a group must kick off simultaneously. The winner and runner up of each groups progresses to the quarter finals, where a knockout system is used (the two teams play each other once, the winner progresses), this is used in all subsequent rounds as well. The winners of the quarter finals matches progress to the semi finals, where the winners play in the final. If in any of the knockout rounds after normal playing time, the scores are still equal, extra time and penalties are employed to separate the two teams.

Football in Norway

Football is the most popular sport in Norway. The Football Association of Norway was founded in 1902 and the first international match was played in 1908.

History

In 1885 Christiania Footballclub [sic] the first ever Norwegian club was founded in Oslo, which was formerly known as Christiania. The club played its first match the next year against a group of english sailors, infront of over 2000 spectators. The Football Association of Norway (the NFF), was founded in 1902, and quickly established a cup competition. After the NFF joined FIFA in 1908, Norway had its first ever international match, away against Sweden in Gothenburg, despite Norway taking the lead after a mere 45 seconds, Sweden went on to win 11-3. In 1911 Norway hosted its first international in Oslo, again against Sweden, this time Norway lose 4-0. In 1912 the Norwegian national football team attended the Olympic games, and were knocked out after losing to Denmark and Austria 7-0 and 1-0 respectively. The NFF hosted the FIFA congress in Oslo in 1914, where a national leage was established with six teams competed for the title Drafn, Frigg, Kvik/Halden, Larvik Turn, Mercantile and Odd, who went on to be the first league winners. The Norwegian national mens team won their only medal at an international championship in 1935 at the Germany Olympic Games. In the relatively succesful tournament Norway beat Turkey and hosts Germany 4-0 and 2-0 respectively, losing to Italy in the semi-final , then beating Poland 3-2 in the third-place play-off to take the bronze medal. The team is known in Norway as "Brogenslat" meaning the Bronze team.

The Football Association of Norway

The Football Association of Norway (NFF) (Norwegian: Norges Fotballforbund) is the governing body of football in Norway. It was formed in 1902. It organises the men's and women's national teams and the Norwegian Premier League. The current president of the NFF is Sondre Kåfjord, while the General Secretary is Karen Espelund. By January 1st, 2004, there are 1,814 clubs organized in Norway, and 373,532 registered players.

The NFF joined FIFA in 1908, and UEFA in 1954.

League system

The current national league system administered by the football association is organised as 1-1-4-24, where Tippeligaen is the highest Norwegian level and Adeccoligaen the second highest, followed by four third level (Division 2) and 24 fourth level (Division 3).

2.5 teams promote from Adeccoligaen to Tippeligaen. The third last team in Tippeligaen play play-off matches against the third best team in Adeccoligaen. 4 teams, the winner of each group, promote from Division 2 to Adeccoligaen. 12 teams (12 of the 24 group winners) promote from Division 3 to Division 2. The group winners play play-off matches.

Level	League(s)/Division(s)
1	Tippeligaen 14 clubs
2	Adeccoligaen 16 clubs
3	Division 2 Group 1 14 clubs			Division 2 Group 2 14 clubs			Division 2 Group 3 14 clubs			Division 2 Group 4 14 clubs
4	Division 3 Group 1 12 clubs	Division 3 Group 2 12 clubs	Division 3 Group 3 12 clubs	Division 3 Group 4 12 clubs	Division 3 Group 5 12 clubs	Division 3 Group 6 12 clubs	Division 3 Group 7 12 clubs	Division 3 Group 8 12 clubs	Division 3 Group 9 12 clubs	Division 3 Group 10 12 clubs	Division 3 Group 11 12 clubs	Division 3 Group 12 12 clubs
4	Division 3 Group 13 12 clubs	Division 3 Group 14 12 clubs	Division 3 Group 15 12 clubs	Division 3 Group 16 12 clubs	Division 3 Group 17 12 clubs	Division 3 Group 18 12 clubs	Division 3 Group 19 12 clubs	Division 3 Group 20 12 clubs	Division 3 Group 21 12 clubs	Division 3 Group 22 12 clubs	Division 3 Group 23 12 clubs	Division 3 Group 24 12 clubs
5–9	Division 4 through Division 8 are regional divisions administered by the various regional football associations.

Cup system

Main article: Norwegian football cup

National team

Main article: Norway national football team

Timelines

Premier League Timeline

FIFA World Rankings Timeline

Elo World Football Timeline

Table

Start Date	Nation	# of days
November 30, 1872	England	1190
March 04, 1876	Scotland	5845
March 05, 1892	England	21
March 26, 1892	Scotland	7
April 02, 1892	England	4349
February 29, 1904	Scotland	12
March 12, 1904	England	2563
March 19, 1911	Netherlands	371
March 24, 1912	England	97
June 29, 1912	Netherlands	3
July 02, 1912	Denmark	2979
August 28, 1920	Uruguay	1
August 29, 1920	Netherlands	3
September 01, 1920	Uruguay	5
September 06, 1920	Spain	12
September 18, 1920	Uruguay	386
October 09, 1921	Spain	959
May 25, 1924	Czechoslovakia	1
May 26, 1924	Uruguay	446
August 15, 1925	Spain	4
August 19, 1925	Uruguay	39
September 27, 1925	Spain	384
October 16, 1926	Argentina	8
October 24, 1926	Uruguay	583
May 29, 1928	Argentina	1
May 30, 1928	Uruguay	382
June 16, 1929	Argentina	96
September 20, 1929	Uruguay	42
November 01, 1929	Argentina	610
July 04, 1931	Uruguay	5
July 09, 1931	Argentina	1053
May 27, 1934	Austria	10
June 06, 1934	Italy	2090
February 25, 1940	Argentina	144
July 18, 1940	Italy	209
February 12, 1941	Argentina	417
April 05, 1942	Italy	50
May 25, 1942	Argentina	229
January 09, 1943	Italy	85
April 04, 1943	Argentina	98
July 11, 1943	Italy	178
January 05, 1944	Argentina	3
January 08, 1944	Italy	367
January 09, 1945	Argentina	33
February 11, 1945	Italy	4
February 15, 1945	Argentina	142
July 07, 1945	Italy	127
November 11, 1945	Argentina	39
December 20, 1945	Italy	735
December 25, 1947	Argentina	1907
March 15, 1953	Brazil	4
March 19, 1953	Argentina	251
November 25, 1953	Hungary	949
July 01, 1956	Argentina	77
September 16, 1956	Hungary	193
March 28, 1957	Argentina	9
April 06, 1957	Hungary	67
June 12, 1957	Argentina	116
October 06, 1957	Hungary	77
December 22, 1957	Argentina	105
April 06, 1958	Hungary	67
June 12, 1958	Brazil	637
March 10, 1960	Argentina	50
April 29, 1960	Brazil	27
May 26, 1960	Argentina	3
May 29, 1960	Brazil	1036
March 31, 1963	Soviet Union	391
April 25, 1964	Hungary	35
May 30, 1964	Brazil	4
June 03, 1964	Argentina	389
June 27, 1965	Hungary	7
July 04, 1965	Brazil	56
August 29, 1965	Argentina	231
April 17, 1966	Brazil	3
April 20, 1966	Argentina	52
June 11, 1966	Brazil	6
June 17, 1966	Argentina	5
June 22, 1966	Brazil	23
July 15, 1966	Argentina	1
July 16, 1966	Soviet Union	9
July 25, 1966	West Germany	5
July 30, 1966	England	1408
June 07, 1970	Brazil	752
June 28, 1972	West Germany	11
July 09, 1972	Brazil	129
November 15, 1972	West Germany	91
February 14, 1973	Brazil	484
June 13, 1974	West Germany	9
June 22, 1974	Brazil	11
July 03, 1974	West Germany	465
October 11, 1975	Poland	4
October 15, 1975	West Germany	960
June 01, 1978	Netherlands	6
June 07, 1978	West Germany	3
June 10, 1978	Netherlands	1
June 11, 1978	West Germany	3
June 14, 1978	Brazil	504
October 31, 1979	West Germany	434
January 07, 1981	Brazil	25
February 01, 1981	West Germany	21
February 22, 1981	Brazil	66
April 29, 1981	West Germany	13
May 12, 1981	Brazil	155
October 14, 1981	West Germany	243
June 14, 1982	Brazil	486
October 13, 1983	Soviet Union	335
September 12, 1984	France	232
May 02, 1985	Soviet Union	34
June 05, 1985	West Germany	7
June 12, 1985	France	91
September 11, 1985	Soviet Union	161
February 19, 1986	France	103
June 02, 1986	Soviet Union	7
June 09, 1986	France	16
June 25, 1986	Brazil	4
June 29, 1986	Argentina	346
June 10, 1987	Brazil	23
July 03, 1987	England	57
August 29, 1987	Soviet Union	74
November 11, 1987	England	214
June 12, 1988	Soviet Union	5
June 17, 1988	West Germany	1
June 18, 1988	Soviet Union	7
June 25, 1988	Netherlands	715
June 10, 1990	West Germany	9
June 19, 1990	Brazil	5
June 24, 1990	West Germany	129
October 31, 1990	Germany	604
June 26, 1992	Netherlands	75
September 09, 1992	Brazil	37
October 16, 1992	Argentina	247
June 20, 1993	Germany	49
August 08, 1993	Argentina	7
August 15, 1993	Germany	313
June 24, 1994	Brazil	3
June 27, 1994	Germany	12
July 09, 1994	Brazil	708
June 16, 1996	Germany	3
June 19, 1996	Brazil	4
June 23, 1996	Germany	311
April 30, 1997	Brazil	30
May 30, 1997	Germany	11
June 10, 1997	Brazil	397
July 12, 1998	France	328
June 05, 1999	Brazil	389
June 28, 2000	France	708
June 06, 2002	Argentina	1
June 07, 2002	France	4
June 11, 2002	Netherlands	1
June 12, 2002	Spain	4
June 16, 2002	Netherlands	5
June 21, 2002	Brazil	351
June 07, 2003	Netherlands	4
June 11, 2003	Brazil	8
June 19, 2003	Netherlands	83
September 10, 2003	France	291
June 27, 2004	Czech Republic	4
July 01, 2004	France	10
July 11, 2004	Brazil	3
July 14, 2004	France	35
August 18, 2004	Argentina	290
June 04, 2005	Czech Republic	4
June 08, 2005	Argentina	21
June 29, 2005	Brazil	102
October 09, 2005	Netherlands	3
October 12, 2005	Brazil	265
July 04, 2006	Italy	43
August 16, 2006	France	-

Wiki Timeline

Heysel Stadium disaster

In 1984 the, liverpool reached the champions league cup final, which was, by a coincedental technicallity, against AS Roma at their home ground of Stadio Olimpico. After a close^[3] match that failed to seperate the two teams, Liverpool won the cup on penalties. After the match, gangs of Roma fans set out and assaulted liverpool supporters who were making there ways back to their hotels^[3]. Many fans were attacked, stabbed and slashed, and one boy who was particularly badly attacked, recquired 200 stitches in his face alone^[3]. Many fans were refused entry to their hotels or guest houses, fearing that the mobs would attack their premises^[3]. The Italian police did little to calm the situation, and many attacked and robbed the english supporters, in revenge for the local teams defeat to liverpool^[3]. Many English fans who had been refused travel to the airport by coach drivers fearing the marauding gangs, ^[3] sought refuge in the British Embassy. After the events of Rome 1984, english hooligans put aside their differences when Liverpool met Juventus in the 1985 final, and sought to deal retribution of their own kind, its claimed that alot of the most notorious english firms were ther, including MIGS from Luton, Bushwackers from Millwall, the ICF from West Ham and the Gremlins from Newcastle^[3].

FIFA World Rankings *

The FIFA World Rankings is a ranking system for national teams in football (soccer). The teams of the member nations of FIFA (Fédération Internationale de Football Association), football's world governing body, are ranked based on their game results with the most successful teams being ranked highest. A point system is used, with points being awarded based on the results of matches played in FIFA-recognized international competitions. Under the existing system, rankings are based on a team's performance over the last eight years, with more recent results being more heavily weighted to help reflect the current competitive state of a team. Teams delivering consistently good performances tend to be more highly ranked, and the system currently in use is somewhat slow to respond to significant changes in a team's performance. A new system, based on results over only four years, and with other amendments to the criteria, has been introduced after the 2006 World Cup. The first edition of the new series of rankings was issued on 12 July 2006.

Other alternative systems have been devised, such as the World Football Elo Ratings, based on the Elo rating system used in chess, ranking teams on an all time basis. The UFWC (Unofficial Football World Championships) ranks teams on the number of times they have defended the Unofficial Football World Championship, an award devised solely for that purpose.

Top 20 Rankings as of July 2006

Rank	Team	Points
1	Brazil	1630
2	Italy	1550
3	Argentina	1472
4	France	1462
5	England	1434
6	Netherlands	1322
7	Spain	1309
8	Portugal	1301
9	Germany	1229
10	Czech Republic	1223
11	Nigeria	1149
12	Cameroon	1109
13	Switzerland	1028
14	Uruguay	985
15	Ukraine	961
16	United States	933
17	Denmark	927
18	Mexico	924
19	Paraguay	915
20	Ivory Coast	909

History

FIFA World
Ranking Leaders

In August 1992 FIFA, working in co-operation with sponsor Coca-Cola, introduced a ranking system for senior national teams intended to provide a fair basis of comparison of the relative strengths of these teams.^[4] This system has been used by FIFA ever since and has seen some major changes to the calculation principles in its short history. The most significant changes were implemented in 1999, in order to allow FIFA's system to compete with the Elo ratings, which were considered a more accurate, credible depiction of the teams' rankings.

1999 update

When the rankings were initially introduced, a team received one point for a draw and three for a victory in FIFA-recognized matches - much the same as a traditional league scoring system. This was a quite simplistic approach, however, and FIFA quickly realised that there were many factors affecting international matches. In order to meet the objective of fairly and accurately comparing the relative strengths of various national sides, the system was updated. The major changes were as follows:

the point ranking was scaled up by a factor of ten
the method of calculation was changed to take into account factors including:
- the number of goals scored or given up
- whether the match was played at home or away
- the importance of a match or competition
- regional strength
a fixed number of points were no longer necessarily awarded for a victory or a draw
match losers were able to earn points

Two new awards were introduced as part of the system:

Team of the Year
Best Mover of the Year

The changes made the ranking system more complex, but helped improve its accuracy by making it more comprehensive.

2006 update

FIFA announced that the ranking system would be updated following the 2006 World Cup. The evaluation period has been cut from eight to four years and the rankings will be based on a simplified method of calculation.^[5] Goals scored and home or away advantage is no longer be taken into account, and other aspects of the calculations, including the importance attributed to different types of match, have been revised. The revised rankings — and calculation methodology — were announced on 12 July 2006.

This change is rooted at least in part in widespread criticism of the previous ranking system. Many football enthusiasts felt it was inaccurate — especially when compared to other ranking systems — and that it was not sufficiently responsive to changes in the performance of individual teams. The recent and unexpectedly high rankings of teams from the Czech Republic and the United States were generally met with skepticism and negatively affected the credibility of the system in the eyes of many followers of the sport. The poor showings and early exit of these two sides from the 2006 World Cup competition appears to lend some credence to the criticism.

Rank leaders

When the system was introduced, Germany debuted as the top ranked team following their extended period of dominance in which they had reached the three previous FIFA World Cup finals, winning one of them. Brazil took the lead in the run up to the 1994 FIFA World Cup, after winning eight and losing only one of nine qualification matches, while on the way scoring twenty goals and conceding just four. Italy then led for a short time on the back of their own equally successful World Cup qualifying campaign, after which the top place was re-claimed by Germany.

Brazil's success in their lengthy qualifying campaign returned them to the lead for a brief period. Germany led again during the 1994 World Cup, until Brazil’s victory in that competition gave them a large lead that would stand up for nearly seven years, until they were surpassed by a strong France team that captured both the 1998 FIFA World Cup and the 2000 European Football Championship. Success at the 2002 FIFA World Cup restored Brazil to the top position, where they have remained ever since on the strength of a Copa América 2004 victory and their continued dominant play^[6]. Italy rise to second following their FIFA World Cup victory, and within 100 hundred points of Brazil, who played poorly in the competition, Italy are possible challengers for the leader position.

Uses of the rankings

The rankings are used by FIFA to rank the progression and current ability of the national football teams of its member nations. The data is used by FIFA for very few things, as FIFA says they are only to create "a reliable measure for comparing national A-teams".^[4] However, one task they are used for is as part of the calculation to seed competitions.^[7] The rankings are also used to determine the winners of the two annual awards national teams receive on the basis of their performance in the rankings.

Seeding in the 2006 World Cup

Below is a table showing how the rankings (current and past standings) were used in combination with the previous World Cup performances of national teams, to determine their seeds for the 2006 FIFA World Cup.^[1] It uses the points obtained from the 1998 FIFA World Cup and the 2002 FIFA World Cup averaged in a 1:2 ratio respectively, added to the average amount of points that each team has at three given dates (at ratio 1:1:1), December 2003, December 2004, and November 2005. This generates a view to how well the teams have performed over the last ten years (since the rankings in 2003 include results from eight years previous to that) with a specific focus on how the teams have performed in the FIFA World Cup on previous occasions. If a team did not qualify for the previous two World Cups, their final total will be significantly less, hence the Czech Republic received a low score for seeding, despite being ranked sixth, fourth, and second in the world at the given dates.

Seed	Country	1. FIFA World Cup Finals					2. FIFA World Rankings							Total Points
		France '98 (33.3%)		Korea Japan '02 (66.7%)		Avg. Points	Dec '03 (33.3%)		Dec '04 (33.3%)		Nov '05 (33.3%)		Avg. Points
		Rk	Pt.	Rk	Pt.	Avg. Points	Rk	Pt.	Rk	Pt.	Rk	Pt.	Avg. Points
1	Brazil	2	31	1	32	31.7	1	32	1	32	1	32	32.0	64
2	England	9	24	6	27	26.0	8	25	8	25	9	24	24.7	51
3	Spain	17	9	5	28	21.7	3	30	5	28	6	27	28.3	50
. . .
16	Czech Republic	-	0	-	0	0.0	6	27	4	29	2	31	29.0	29

Criticism

Since their introduction in 1993, the FIFA World Rankings have been the matter of much debate, particularly regarding the calculation procedure and the resulting disparity between generally perceived quality and world ranking of some teams. For example Norway was ranked second in October 1993 and July-August 1995,^[8] and the United States reached fourth, to the surprise of even their own players. ^[9]

Pre-tournament betting odds for 2006 FIFA World Cup^[10]^[11]^[12] show enormous discrepancy between the comparative likelihood of victory in the tournament and the FIFA rankings at the beginning of the tournament, particularly for Germany, Ukraine, the USA and Iran. Comparison of one betting table with the rankings list gives Spearman's ρ=0.69.

One thing that has been criticised^[13] is that the rankings consider the performances of teams over an eight year period, and that teams' ranking positions do not correlate to their recent performances.^[8] This criticism should lessen with the introduction of a new formula, reflecting results over a four year period, from July 2006.

The perceived flaws in the FIFA system has lead to the creation of a number of alternative rankings from football statisticians^[8] including the World Football Elo Ratings and the rec.sport.soccer Statistics Foundation rankings.

FIFA's change of system for calculation of these rankings and their adoption of a different formula for World Cup seedings may be seen as an implicit admission of the shortcomings of the current formula.

How the rankings have changed

The current calculation method

Overview

After the 2006 FIFA World Cup, a new revised calculation procedure for the FIFA rankings was introduced; it is a significantly simplified procedure. The new rankings were compiled in response to criticism from the media.^[4] Meetings were attended by FIFA staff and external experts an a large amount of research was conducted by this group, that resulted in the new rankings,^[4] the new system maws confirmed in Leipzig, on the 7 December 2005 by a committee of FIFA executives. Notable changes include the complete dropping of the home or away advantage and number of goals from the calculation altogether.

The system, as all the previous ones is extremely similar to that of a league, though with changes made to ensure that it is still representative of the teams performance despite the differing number of matches per annum, and the differing strength of opposition that teams have to face. The factors taken into account are as follows;

Match result
Match status
Opposition strength
Regional strength determined by confederation weightings

Matches within the previous four ear period are included in the calculation; matches after that period are not used in the procedure.

Win, draw or defeat

Whereas in previous years a complicated system of points allocation was used depending on how strong the opponent was, and how large the loss margin, even allowing weaker losing teams to gain points when playing a much stronger opposition, if they managed to put up a decent match. Now, the points allocation is simple, three points for a win, one point for a draw, and zero points for a loss, this is exactly the same as all league systems.

In the event of a match being decided by a penalty shootout, the winning team receives two points, and the loser’s one (which for the losers is the same as the draw which they earned).

Match status

Different matches have different importance to teams, and FIFA has tried to respect this by using a weighting system. Where the most weighted, and therefore regarding the rankings, considered the most important matches, are world cup matches. The lowest weighted ones are friendlies, however FIFA states that it wishes to recognise that friendlies are still important, since they make up of half of the competitive matches counted in the rankings.^[14]

The weighting multipliers are as follows;

Friendly
FIFA World cup and Continental cup qualifiers
Continental cup, and Confederations Cup finals
World cup finals

—
—
—
—

1.0
2.5
3.0
4.0

Opposition strength

Regional strength

Confederation weightings

Assesment Period

Summary

Examples

Calculation method from 1999 - 2006

The FIFA world rankings are fundamentally the same as a league system, though on a much larger, and more complex scale. Each team can potentially win a certain number of points in each match, though the number of points awarded, in a league system depends solely on the result of the match, in the FIFA rankings far more has to be taken into account, as every team does not play all of the other teams home and away every season, as in most league systems. After the awarding of points, the teams are then organized into descending order by the number of points, with the team with the most, being the highest ranked.

The points allocated did not depend solely on whether a team wins, loses or draws their match, but also on the importance of the match and the strength of the opponent. A win over a weak opponent will result in less points being awarded than a win over a much stronger one. This means that a match will not result in the two or three points for a win and one for a draw, as is standard in most national league competitions. The calculation is more complex since it has to incorporate the other aforementioned factors.^[4]

Since the Rankings were revised in 1999 changes have taken place, one of which FIFA has dubbed the "scaling up", where the points on offer for a match have been roughly multiplied by ten, with the addition of more factors. Now teams can receive between zero and thirty points for a single match, and the leaders of the rankings have over eight hundred points.

Overview

The system explained is the one used to calculate the rankings from 1999 to 2006. This revision was be replaced with a newer one following the 2006 FIFA World Cup.

The rankings were intended by FIFA to give a fair ranking of all FIFA member associations’ senior national teams. For the ranking all matches, their scores and importance were all recorded, and were used in the calculation procedure. Only matches for the senior national team were included, separate rankings were used for other representative national sides, such as the woman’s and junior teams, for example the FIFA Women's World Rankings. Interestingly, FIFA did not use the same formula to determine its rankings for women's football. The women's rankings are based on a procedure which is a simplified version of the Football Elo Ratings.^[15]

For the purposes of calculating the importance of matches, each match was divided into one of six categories. Competitions that were not endorsed by the appropriate continental association of FIFA are counted as friendlies. Each category is given appropriate weighting in the calculation in order to correctly include the importance. The six categories were:

World Cup finals matches
World Cup preliminary matches
FIFA Confederations Cup matches
Continental championships final matches
Continental championship preliminary matches
Friendly matches

A computer program was used to calculate the rankings, points were awarded according the following criteria:

Winning, drawing and losing
Importance of the match (multiplication factor)
Regional strength (multiplication factor)

In order to try and remove the obvious advantage of having more matches, only the best seven matches each year were taken into account, as seven was the average number of matches a team plays per year. Older matches were given diminishing importance within the calculation, in order to reward teams most recent form,^[4] until after eight years, they were completely discarded, so the calculations only take into account teams performances over the last eight years.

At the end of each season two prizes were awarded by FIFA; Team of the Year and Best Mover of the year.

Winning, drawing or losing

In any football ranking system, a win will bring more points than a draw or a loss. Until July 2006, however, FIFA believed awarding points simply on the basis of win, draw or loss, would not meet the requirements of a reliable and accurate world ranking system.

From July 2006, three points will be awarded for a win, one point for a draw, and no points for a loss but in order to create a better ranking system, the calculations will also take into account the relative strengths of the two teams. This results in more points being awarded for beating a stronger opponent, than a relatively weaker one. It also enables weak teams to earn points despite a defeat if they manage to play well (i.e. they score goals, or there is low margin of defeat), though this is a small amount and will not secure as many points as the team that beat them. In the event of a match being decided on penalties, the winners will receive the correct points for the victory. The losers will receive points for the draw which they earned in normal time.

Number of goals

When calculating the points, the number of goals is taken into consideration, and once again, the distribution of the points between the two teams is also affected by their relative strengths (i.e. the lower ranked a team is in comparison to its opponent, the more points it receives for a goal scored), and as well as points being given for goals scored, they are deducted from the total for conceding. In order to encourage more attacking football, points given for goals scored are weighted far more heavily than the deduction as a result of conceding, though most teams are more concerned with the tournament or match at hand than their position in the world rankings. When a match is decided on penalties, only those scored in playing time are included in the total.

To prevent "overweighing" goals, and huge amounts of points being dealt in runaway victories, far more weighting is attached to the initial goal by each team, and progressively less points for any subsequent ones. This is done in the agreement that the goals scored are important but the most important factor is the win or loss, as in normal championship games.

Home and away games

To allow for the extra handicap incurred by playing away from home, a small bonus of three points per match is awarded to the away team. Note that to prevent this from affecting the points dealt in tournaments played on neutral territory, but with a home team, such a World Cup Finals, there are no bonus points given.

Status of a match

The relative game importance is also considered when calculating the points. The method for incorporating this into the totals points’ allocation is by multiplying the match points by a predetermined weighting. These factors are:

Factor	Weighting
Friendly match	x 1.00
Continental championship preliminary	x 1.50
World Cup preliminary match	x 2.50
Continental championship finals match	x 3.00
FIFA Confederations Cup match	x 3.00
World Cup finals match	x 4.00

Regional strength factors

As between the various continents there are quite significant differences in national team strengths, weighting factors are worked out each year for each confederation. The basis of the evaluation and resulting factors is the member teams of the confederation's performances in intercontinental encounters and competitions, at the end of every season, a continental ranking list is calculated, based on the same criteria as the FIFA rankings. Not all the intercontinental matches are taken into account, but only matches between the strongest 25 percent of teams from each continent, with a minimum of five teams from each continent considered. This way errors that could be caused by considering matches where relatively strong teams from one confederation defeat weak teams from another, are averted.

The weightings (shown below) are applied in the form of multiplication factors for teams from the same continent. If teams from two different confederations are involved in one match then the factor applied is the average of the two continental weightings.

For 2005, the following weighting factors were applied:

Federation	Weighting
UEFA	x 1.00
CONMEBOL	x 0.99
CAF	x 0.96
CONCACAF	x 0.94
AFC	x 0.93
OFC	x 0.93

After the 2006 FIFA World Cup, these weighting factors were amended. They now reflect the number of wins each confederation has recorded against other confederations at the last three World Cups.

Federation	Weighting
UEFA	x 1.00
CONMEBOL	x 0.98
CONCACAF	x 0.85
AFC	x 0.85
CAF	x 0.85
OFC	x 0.85

Summary

Based on the above considerations, the total number of points credited to a team after a match will depend on the following criteria:

Where:

w = Points for winning, drawing or losing
g = Points for goals scored in this game
c = Points for the goals conceded
a = Bonus for the away team
s = Appropriate factor for the status of the match
r = Appropriate factor for regional strength
m = Points Received

( w + g + a − c ) s r = m

The number of points for a win, draw or loss, as well as for the number of goals scored or conceded is dependent on the strength of the opponent. In order not to punish a lack of success too severely, a negative points total is rounded up to 0.00.^[4]

These examples have also been used on the Elo football ratings for a fair comparison. Here are some calculation examples to show the formula being used. For simplicity in this instance it is assumed that three teams of different strengths are involved in a small friendly tournament on neutral territory.

Note:no away team bonus, nor continental or status multiplication factors are applied.

Before the tournament the three team have the following point totals:

Team	Points
A	630
B	500
C	480

As shown, team A is by some distance the highest ranked of the three: The following table shows the divisions of point allocations based on three possible outcomes of the match between the far stronger team A, and the somewhat weaker team B:

Example 1

Team A versus Team B (Team A stronger than Team B)

	Team A	Team B	Team A	Team B	Team A	Team B
Score	3 : 1		1 : 3		2 : 2
Points for Win/defeat	+17.4	+2.6	-2.6	+22.6	+7.4	+12.6
Points for Goals Scored	+5.4	+2.7	+2.3	+6.2	+4.1	+4.7
Points for Goals Conceded	-1.8	-3.6	-4.1	-1.6	-3.1	-2.7
Total	+21.0	+1.7	(0.00)	+27.2	+8.4	+14.6

As is shown on the table, in the case of a 3:1 win, team a receives an allocation of 21.0 points, however, since team A is a much higher ranked team, the win alone earns only 17.4 of the total points, and the much lower ranked team B still manages to earn 1.7 points. Had match been won 3:1 by the far weaker team B, they would have received 27.2 points, whilst team A would have received a negative total of points, which would then have been rounded up to 0.0. If the result had been a 2:2 draw, since it is the lower-rated team, B would have earned a few points more than team A.

Example 2

Team B versus Team C (both teams approximately the same strength)

When the difference in strength between the two teams is less, so also will be the difference in points allocation. The following table shows how the points would be divided following the same results as above, but with two roughly equally ranked teams, B and C, being involved:

	Team B	Team C	Team B	Team C	Team B	Team C
Score	3 : 1		1 : 3		2 : 2
Points for Win/defeat	+19.4	+0.4	-0.4	+20.4	+9.6	+10.4
Points for Goals scored	+5.7	+2.5	+2.5	+5.8	+4.3	+4.4
Points for Goals conceded	-1.7	-3.8	-3.9	-1.7	-3.0	-2.9
Total	+23.6	(0.00)	(0.00)	+24.5	+10.9	+11.9

As is shown in the .

Comparison with Elo ratings

Assuming team B drew with team A and lost to team C the table now stands (decimals rounded);

Team	Initial Points	Final Points (FIFA)	Rank (FIFA)	Final Points (Elo)	Rank (Elo)
Team A	630	638	=	626	=
Team B	500	515	=	493	-1
Team C	480	505	=	496	+1

As you can see, as the criticism suggests, the FIFA rankings have been slow to respond to Team Bs considerable drop in form, with despite Team Cs underdog victory, the margin between it and Team B is still ten points, whereas in the Elo rankings, team C has overtaken team B. Also in the FIFA rankings, team A despite having drawn with a team significantly lower ranked than itself, has still gained 8 points, whereas in the Elo rankings has lost 4. However in the Elo rankings, team B who managed a draw with significantly higher ranked team A, have lost a position in the rankings due to only a single poor result, and have overall lost almost ten points.

Further criteria

To increase the level of accuracy and objectivity of the rankings, after the 1999 revision further criteria was introduced. Firstly, the number of matches a team plays within a given period of time would be taken into account. Secondly, the importance attached to previous results would be interpreted differently.

The number of matches played

In order to ensure that an increased number of fixtures in a given season does not give a team more potential points, the rankings only consider a limited amount of results. This amount was determined by deciding how many fixtures in a season an "averagely active team" would participate in, this was agreed to be between seven and ten matches a year.

In order to prevent teams with fewer fixtures than this been disadvantaged, the calculation initially considers only the best seven results of a team. To include further results an average of them must be calculated.

For example, if a team played twelve matches, the calculation would run as;

The best seven of the 12 results are identified
The total score for these seven matches is calculated (X)
The total score for all 12 matches is calculated
This total is divided by 12 and multiplied by seven (Y)
The total for the seven best results is added to the seven "average" results (X+Y)
This total (X+Y) is divided by two for the final score

Previous results

In order to assure that the rankings best reflect team’s current form, the most recent results are of greatest importance; however attention is also paid to the results of previous years. The results from the preceding year are given full weighting, with the results from two years before given seven eighths of their value, those from three years before given six eighths, and so on until after eight years the results are dropped from calculation completely.

Calculation method from 1993 - 1999

Overview

Points awarded for winning, drawing or losing

Opponent strength

Home or away

Match importance

Regional strength

Summary

Examples

Awards

Each year FIFA hands out two awards to its member nations, based on their performance in the rankings. They are;

Team of the Year

Team of the Year is awarded to the team whose best seven matches of the year received the most amount of points overall.

Best Mover of the Year

Best Mover of the Year is awarded to the team who has made the best progress up the rankings over the course of the year. In the FIFA rankings, this is not simply the team that has risen the most places, but a calculation is performed in order to account for the fact that it becomes progressively harder to earn more points the higher up the rankings a team is.^[4] The calculation used is the number of points the team has at the end of the year (z) multiplied by the number of point it earned during the year (y). The team with the highest index on this calculation receives the award. The table below shows the calculation for this award in 2002.

Rank	Team	Points at end of 2002(z)	Points won in 2002 (y)	Score (z × y)
1	Senegal	646	107	69122
2	Wales	554	113	62602
3	Brazil	856	63	53928
4	Cameroon	685	76	52060
5	Mali	490	99	48510

References

^ ^a ^b "MapsofWorld.com - 2006 FIFA World Cup - Entire FIFA Seeding of the Teams participating in 2006 FIFA World Cup Finals". MapsofWorld.com. 31 May 2006. {{cite news}}: Text "http://www.mapsofworld.com/2006-fifa-world-cup/fifa-world-soccer-rankings.html" ignored (help) Cite error: The named reference "MapsofWorld2" was defined multiple times with different content (see the help page).
^ "UEFA Euro 2004 Final Match Day Publication". UEFA. July 4th 2006. p. 59. {{cite news}}: Check date values in: |date= (help)
^ ^a ^b ^c ^d ^e ^f ^g "The Heysel Tragedy". {{cite news}}: Unknown parameter |access date= ignored (|access-date= suggested) (help)
^ ^a ^b ^c ^d ^e ^f ^g ^h "FIFA/Coca-Cola World Rankings". FIFA. 30 May 2006.
^ "Great expectations". FIFA. 24 May 2006.
^ "Brazil riding the wave". FIFA. 18 Jan 2006.
^ "FIFA Seeding of the Teams participating in 2006 FIFA World Cup Finals". MapsofWorld.com. 31 May 2006.
^ ^a ^b ^c "The world rankings riddle". BBC. 21 December 2000.
^ "FIFA adapting new world rankings". Associated Press. 02 June 2006. {{cite news}}: Check date values in: |date= (help)
^ "World Cup Odds". 02 June 2006. {{cite news}}: Check date values in: |date= (help)
^ "World Cup odds". Centrebet. 02 June 2006. {{cite news}}: Check date values in: |date= (help)
^ "Outright Win & Place odds in World Cup 2006". IASbet.com. 02 June 2006. {{cite news}}: Check date values in: |date= (help)
^ "FIFA Rankings". Travour.com. 01 June 2006. {{cite news}}: Check date values in: |date= (help)
^ "The new FIFA rankings in focus" (PDF). FIFA. July 2006.
^ "FIFA Women's World Ranking Methodology". FIFA. 30 May 2006.

External links

History of football (soccer)

The history of football begins in ancient civilisations, with similar ball based sports being present, though modern association football as we know it comes from England, where a group of schools of football laid down the first universally excepted rules in 1863. They also agreed to set up the FA the first football association in the world, and football spread throughout the British Isles. Later other countries followed suit. International tours of English football teams around the world helped spread it to all of the continents which had countries that were formerly part of the British Empire.

Origins of the Game

From ancient games to the late middle ages

Association football was first played in an organised fashion over a century ago. The exact origins of the game are unknown, but with many ball based games being played through history including Harpustum by the Romans (which had developed from the Ancient Greeks Episkyros), Tsu Chu by the ancient Chinese and Kemari by the Japanese. The ancient Chinese game of Tsu Chu is commonly believed to have been in the Tsin Dynasty, (255-260BCE) however there are a number of opinions on the dates involved, some go all the way back to 5000 BCE^[1] . The game of Association Football as we know it today is most likely to have originated from the Roman game Harpustum (Latin for Handball), which was imported to Britain when the Romans invaded.

Harpustum was a game which is thought to have been played by the legions as they awaited there return to Italy, is as the translation suggests, far more similar to today’s rugby, than football, yet both games developed from the same root, after the Romans left, by the 16th Century Harpustum had developed into Calcio, with teams of 26 or 27 men apiece, typically one in green and one wearing red. The game was subject of much betting on the sidelines. The rules of the game, discorsa calcio, were formalised around 1580.

Folk football emerges

Britain developed the formalised rules of Association football, which, by and large, still hold sway over the world’s football. Yet before they were adopted in the 19th century the game had a reputation hooligans and fights, where the participants of the average game outnumbered the spectators. Several of these early fixtures attained status as a sort of annual ritual, such as The Shrove Tuesday contest at Ashbourne in Derbyshire, where one half of the town played the other, where the goals are the parish church at one end of the town, and Ashbourne Hall at the other. This fixture continues to be played annually to this day, as the word spread, other Shrove Tuesday fixtures sprang up, including ones at Corfe Castle in Dorset, and Scone in Scotland.

At the Chester Shrove Tuesday fixture, courtesy of the town’s cobblers, a leather ball was introduced to the game. These 'mob football' games began to spread throughout the country, and typically anyone who turned up played, meaning that the number of participants regularly went over 100, and the goals were several miles apart. Few rules prevailed in mob football this coupled with the uncontrollable numbers of players involved meant that the risk of permanent or debilitating injuries was high. The games were often used as an arena to settle old scores. These factors and the unruly behaviour of the participants meant that among others, Kings, clergyman, womenfolk and the Puritans all attempted to ban the game, all were unsuccessful. Men in the English army of 1365 were banned from playing football when it became apparent they would rather play football than fight. This did apparently improve their archery, but failed to eradicate the game.

Football becomes a leisure of the upper classes

Cambridge University added the game to there curriculum at the turn of the 17th century, this showed a changing public opinion towards the game. With the Industrial Revolution sweeping the country, as by the early 19th century, (before the Factory Act of 1850), most working class people in Britain had to work six days a week, often for over twelve hours a day. They had neither the time nor the inclination to engage in sport for recreation and, at the time, many children were part of the labour force. Feast day football on the public highway was at an end.

So the working classes now had little time or energy to play the game, and it spread to the upper classes, as they were free from the work of the lower classes, as a far more leisurely affair. Ad the public schools began to play it, each laid down its own individual rules, often tailored to where they played the game. Notably Rugby School, positively encouraged handling of the ball, where others did not, however they did not permit movement whilst the ball was being handled, but famously William Webb Ellis paid no regard to this rule, and his legendary run gave rise to the game of Rugby football. This form of football separated from association football in 1848, when a committee held at Cambridge University defined the game as permitting handling only for the purposes of controlling the ball, and furthermore, the goals should consist of two posts. These rules became known as The Cambridge Rules.

English public schools

File:Winchester football (1840).jpg

Match at Winchester College around 1840.

The earliest evidence that games resembling football were being played at English public schools — mainly attended by boys from the upper, upper-middle and professional classes — comes from the Vulgaria by William Horman in 1519. Horman had been headmaster at Eton College and Winchester and his Latin textbook includes a translation exercise with the phrase "We wyll playe with a ball full of wynde". The first specific mention of football can be found in a Latin poem by Robert Matthew, a Winchester scholar from 1643 to 1647. He describes how "...we may play quoits, or hand-ball, or bat-and-ball, or football; these games are innocent and lawful...". Nugae Etonenses (1766) by T. Frankland also mentions the "Football Fields" at Eton.

Football had come to be adopted by a number of public schools as a way of encouraging competitiveness and keeping youths fit. Each school drafted their own rules to suit the dimensions of their playing field. The rules varied widely between different schools and were changed over time with each new intake of pupils. Soon, two schools of thought about how football should be played emerged. Some schools favoured a game in which the ball could be carried (as at Rugby, Marlborough and Cheltenham), whilst others preferred a game where kicking and dribbling the ball was promoted (as at Eton, Harrow, Westminster and Charterhouse). The division into these two camps was partly the result of circumstances in which the games were played. At Charterhouse and Westminster the boys were confined to playing their ball game within the cloisters making the rough and tumble of the handling game difficult.

The boom in rail transport in Britain during the 1840s meant that people were able to travel further and with less inconvenience than they ever had before. Inter-school sporting competitions became possible. While local rules for athletics could be easily understood by visiting schools, it was nearly impossible for schools to play each other at football, as each school played by its own rules.

During this period, the Rugby school rules appear to have spread at least as far, perhaps further, than the other schools' games. For example, it is said that the world's first "football club" (that is one which was not part of a school or university), was the Guy's Hospital Football Club, founded in London in 1843. The club is said to have played the Rugby school game. However, some have argued that this club is too poorly documented to be considered to have existed since that time.

In 1845, three boys at Rugby school were tasked with codifying the rules then being used at the school. These were the first set of written rules (or code) for any form of football.

Perhaps surprisingly for a game now associated with the working class, the separation of Association Football from the other codes, happened at some of Britain’s more upper class public schools, where the wealthy sent their boys to be turned into young gentlemen.

Football organises

The first rules

Cambridge University defined the game as permitting handling only for the purposes of controlling the ball, and furthermore, the goals should consist of two posts, this committee, also defined fouls, they were, tripping, kicking or holding, and an offside rule and an offside rule insisting on three men between the passer and the opposing goal was introduced. With these rules laid down, and the increasing respectability of the game, Sheffield Cricket Club allowed for matches to be played on their pitch at Bramall Lane in the 1850s. And thus, Sheffield F.C. can claim to be Britain's oldest football club^[2] , but to this day, the win of the 1904 FA Amateur Cup, remains as the clubs greatest success.

The first universal rules were laid down on the 26 October, 1863, when eleven southern English clubs each sent representatives to Freemason's Tavern in London. Their intent was to lay down an acceptable form of rules which the game could be played by. They came to the following resolution

"That it is advisable that a football association should be formed for the purpose of settling a code of rules for the regulation of the game of football"^[3]

And the first "annual general meeting of the Football Association", was set for the last week of September that year. This has continued to be the start of the traditional football season ever since. All the clubs that were at the previous meeting could send two representatives to the meeting, if they paid a one guinea subscription. However, all of those present, could not give there full backing to the movement. The first formal rules were agreed by early December, these led to the resignation of Rugby from the association, not on the issue of handling, but on the issue of 'hacking', or physically kicking opponents. The Rugby Football Union was formed in 1871 for those who still played by the rules which allowed handling and hacking.

The rules agreed on by the FA stipulated a maximum length and breadth for the pitch, the procedure for kicking off, and definition of terms, including goal, throw in, offside. Passing the ball by hand was still permitted provided the ball was caught "fairly or on the first bounce". Despite the specifications of footwear having no "tough nails, iron plates and gutta percha" there were no specific rule on number of players, penalties, foul play or the shape of the ball, captains of the participating teams were expected to agree on these things prior to the match.

The foundations are laid for a competition

The Rules laid down by the FA had an immediate effect, with Sheffield and Nottingham (now Notts County) joining playing an annual fixture on the FA code among others. In 1865 Nottingham Forest was founded, and the first derby game took place. Over the next two years Chesterfield and Stoke joined the code. This finally meant that football was no longer an exclusive sport of public schools. However, it was by no means a working class pass time. By this time teams had settled into 11 players each, and the game was played with round balls.

In 1967 the offside rule was altered, it previously stated that all players in front of the ball were offside, eliminating passing of the ball forwards, much like in rugby today. The rule was relaxed. A Sheffield against London game in 1866 had allowed the FA to observe how the rules were affecting the game, subsequently handling of the ball was also abolished except for one player on each team, the goalkeeper. And a red tape between the two goalposts to indicate the top of the goal. Also a national competition was proposed.

The first FA Cup

On July 20, 1871, C. W. Alcock proposed that "a Challenge Cup should be established in connection with the [Football] Association",^[4] the idea that gave birth to the competition .The First FA Cup was played in 1872, Wanderers and Royal Engineers met in the final inform of 2,000 paying spectators. Despite Royal engineers being heavy favourites, one of their players sustained a broken collar bone early on and since substations had not yet been introduced, hence engineers played a man down for the rest of the match which they eventually lost 1-0.

The FA Cup was a success and within a few years all of the clubs in England wanted to take part, to do so they had to accept the FA code, this led to the quick spread of a universal set of rules. These rules are the basis of which all association football rules today stem from.

Later competitions saw the 'Gentleman' or Southerners dominate with Old Etonians, Wanderers, Royal Engineers and Oxford University who amongst them took 19 titles. Queens Park withdrew in the semi-finals of the 1873 cup (which due to the format being played that year meant that they were one the final two who play for the right to throw down the gauntlet and play the holders, hence the full name FA Challenge Cup) because they had trouble raising travel expenses to pay for the constant trips to England, this directly led to the formation of the Scottish FA. However despite this, Queens park continued to participate in the FA Cup, reaching the final twice, before the Scottish FA banned Scottish clubs from entering in 1887.

In 1872, Alcock purchased the Football Association Cup for £20, fifteen clubs entered the competition that year. Queen's park reached the semi finals without playing due to withdrawals, but then after a goalless draw with Wanderers, were forced to withdraw as before the advent of penalties and extra time, they could not afford to come back to London for the replay. Wanderers won the cup outright in 1878 after what remains to this day one of only two hat tricks of wins ever. However they returned the cup to the FA in order for the competition to continue, on the condition that not other club could win the cup outright ever again.

The first International

Charles Alcock, who was elected to secretary of the FA at the age of 28, devised the Idea of an international competition, inaugurating an annual England-Scotland. His put advertisements in papers in Glasgow, informing people of an international between the two countries at Kennington Oval, then the home of Surrey Cricket Club. After the appeal, a team of Scottish players was put together and captained by Robert Smith, one of the three brothers who helped found Queens Park FC. His team which lost the match 1-0 was composed entirely of Scots, living in England. Other the next three annual fixtures at Kennington, the best the Scots could manage was a 1-1 draw, the fourth fixture was played at the home of the West of Scotland Cricket Club in Partick. It was a goalless draw, and so one of the most bitterly disputed fixtures in footballing history was born. The first non-european international was contested between the USA and Canada, the canadians winning 1-0.

From amateur to professional football

When football was gaining popularity during the 1870s and 1880s professionalism was banned in England and Scotland. Then in the 1880s, soon after Wanderers disbanded, in the north of England, teams started hiring players known as 'professors of football', who were professionals from Scotland. This was the first time professionalism got into football. The clubs in working class areas, especially in Northern England and Scotland wanted professional football in order to afford playing football besides working. Several clubs were accused of employing professionals. In 1885 the FA legalized professional football, but with a national wage limit. The northern clubs made of lower class paid players started to gain momentum over the amatuer 'Gentleman Southerners'. The first northern club to reach the FA cup final was Blackburn in 1882, where they lost to Old Etonians, they were the last amateur team to win the trophy.

However a maximum wage was place on players, players challenged this and came close to strike action in 1909, but it was not to be for another fifty years before the maximum wage was abolished.

Hakoah Vienna was probably the first non-English club to pay their players during the 1920s. They were also the first non-English club to beat an English club in England when they beat West Ham 5-1 in 1923.

In 1934 the Swedish club Malmö FF was relegated from the top division after it had been discovered that they paid their players, something that was not allowed in Swedish football at the time.

The first league

In 1888, William McGregor a gentleman from Perthshire was the main force between meetings held in London and Manchester involving 12 football clubs, with an eye to a league competition. These 12 clubs would later become the Football Leagues 12 founder members. The meetings were held in London on 22 March 1888, the main concern was that an early exit in the knockout format of the FA cup could leave clubs with no matches for almost a year, not only could they suffer heavy financial losses, but fans didn't often stick around for that long without a game, when others teams were playing. Matters were finalised on the 17 April in Manchester.

McGregor had voted against the name The Football League, as he was concerned that it would be associated with the Irish Land League^[5]. But this name still won by a majority vote and was selected. The competition guaranteed fixtures and members for all of its member clubs. The clubs were split equally among North and Midlands teams and Southern teams, who were still strictly amateur.

Football spreads around the world

Football reaches Continental Europe

Football was introduced in the Danish club Kjøbenhavns Boldklub in 1879 which makes the club the first football club on Continental Europe. The Danish Football Association was founded in 1889.

Italian football was played in regional groups from its foundation in 1898 until 1929 when the Serie A was organized into a national league by the Italian Football Federation.

La Liga, Spain's national league, had its first season in 1928, with its participants based off of the previous winners of the Copa del Rey, which began in 1902.

The German national league, the Bundesliga was late in foundation, especially for European countries, given it wasn't founded until 1963. Prior to the formation of the Bundesliga, German football was played at an amateur level in a large number of regional leagues. As many countries previously had done.

At the beginning of the 20th century most European countries had a national football association.

Football reaches South America

The first recorded football match in Argentina was played already in 1867 by English railway workers. The Argentine national leagues were founded in 1931 by the Argentine Football Association, which itself was founded by Englishmen in 1893.

In the 1870s an expatriate named Miller (first name unknown) who worked on the railway construction project in Sao Paulo together with some 3000 other immigrant families from the British Isles in the last decades of the 19th century. Mr. Miller decided to send his young boy Charles William Miller to England for his education. In 1884 Charles aged 10 was sent to Bannisters school in Southampton. Charles was a natural footballer who quickly picked up the arts the game. The football association was being formed at the time. Eton, Rugby, Charterhouse and other colleges all had developed their own rules to the game. As an accomplished winger and striker Charles held school honours that were to gain him entry first into the Southampton Club team and then into the County team of Hampshire.

In 1892 a couple of years before his return to Brazil, Charles was invited to play a game for the Corinthians, a team formed of players invited from public schools and universities.

On his return Charles brought some football equipment and a rules book with him. He then went on to develop the new rules of the game amongst the community in Sao Paulo. In 1888 six years before his return the first sorts club was founded in the City, Sao Paulo Athletic Club. Sao Paulo Athletic Club won the first three years championships. Miller’s skills were far and above his colleagues at this stage. He was given the honour of contributing his name to a move involving a deft flick of the ball with the heel "Chaleiro".

Charles Miller kept a strong bond with English football throughout his life. Teams from Southampton and Corinthians Club came over to Brazil and played against Sao Paulo Athletic Club and other teams in Sao Paulo. One on occasion in 1910 a new local team was about to be formed after a tour of the Corinthians team to Brazil and Charles was asked to suggest a name for the team. He suggested they should call themselves after Corintians.

In 1988 when Sao Paulo Athletic Club celebrated its centenary and the English Corinthians Team came across again to play them at Morumbi Stadium. The end of the tour was against the local professional Corinthians Paulista team with Socrates and Rivelino amongst its players. This game was played at Paecambu Stadium in Sao Paulo and true to Corinthian principles of good clean football the score was 1 to 0 in favour of the locals when as agreed Socrates changed shirts to play alongside the English amateurs. This did not affect the score unfortunately although a largely packed stadium was cheering on for a drawn result.

The Brazilian Football Confederation was founded in 1914, and the current format for the Campeonato Brasileiro was established in 1971.

Founding of FIFA

FIFA World Cup

The first football world cup was played in 1930. Many countries did not enter, with most of them coming from the Americas. By 1950 however, european teams took interest, and the competition blossomed into the worlds biggest footballing event. Brazil have won the championship a record 5 times.

References

^ "The Football Network". April 2006.
^ "A History of Football". Green Umbrella Publishing. 2003. p. 13.
^ "A History of Football". Green Umbrella Publishing. 2003. p. 14.
^ "FA official website". The Football Association. January 2005.
^ "A History of Football". Green Umbrella Publishing. 2003. p. 22.

[[Category:Football (soccer)]]

Helpful Notes

footy gets to brazil

general history of footy Bold text

[MapsofWorld2-1] "MapsofWorld.com - 2006 FIFA World Cup - Entire FIFA Seeding of the Teams participating in 2006 FIFA World Cup Finals". MapsofWorld.com. 31 May 2006. {{cite news}}: Text "http://www.mapsofworld.com/2006-fifa-world-cup/fifa-world-soccer-rankings.html" ignored (help) Cite error: The named reference "MapsofWorld2" was defined multiple times with different content (see the help page).

[UEFAEuro2004Final_MatchDayPublication-2] "UEFA Euro 2004 Final Match Day Publication". UEFA. July 4th 2006. p. 59. {{cite news}}: Check date values in: |date= (help)

[bianconeri-3] ^ ^a ^b ^c ^d ^e ^f ^g "The Heysel Tragedy". {{cite news}}: Unknown parameter |access date= ignored (|access-date= suggested) (help)

[FIFAcoke-4] ^ ^a ^b ^c ^d ^e ^f ^g ^h "FIFA/Coca-Cola World Rankings". FIFA. 30 May 2006.

[FIFAcalc-5] "Great expectations". FIFA. 24 May 2006.

[FIFAbrazil-6] "Brazil riding the wave". FIFA. 18 Jan 2006.

[MapsofWorld-7] "FIFA Seeding of the Teams participating in 2006 FIFA World Cup Finals". MapsofWorld.com. 31 May 2006.

[BBCreport-8] "The world rankings riddle". BBC. 21 December 2000.

[GnM-9] "FIFA adapting new world rankings". Associated Press. 02 June 2006. {{cite news}}: Check date values in: |date= (help)

[WS-10] "World Cup Odds". 02 June 2006. {{cite news}}: Check date values in: |date= (help)

[CB-11] "World Cup odds". Centrebet. 02 June 2006. {{cite news}}: Check date values in: |date= (help)

[SFB-12] "Outright Win & Place odds in World Cup 2006". IASbet.com. 02 June 2006. {{cite news}}: Check date values in: |date= (help)

[travour-13] "FIFA Rankings". Travour.com. 01 June 2006. {{cite news}}: Check date values in: |date= (help)

[FIFArnk06-14] "The new FIFA rankings in focus" (PDF). FIFA. July 2006.

[FIFAwomens-15] "FIFA Women's World Ranking Methodology". FIFA. 30 May 2006.

[footballnetwork-16] "The Football Network". April 2006.

[AHistoryOfFootball13-17] "A History of Football". Green Umbrella Publishing. 2003. p. 13.

[AHistoryOfFootball14-18] "A History of Football". Green Umbrella Publishing. 2003. p. 14.

[FA.comonFAcup-19] "FA official website". The Football Association. January 2005.

[AHistoryOfFootball22-20] "A History of Football". Green Umbrella Publishing. 2003. p. 22.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[1]

[2]

[3]

[4]

[5]

Random

Partial Differentiation

Usage

Ref Desk Q's

electrons

data handling

sense proj

Silicon proj

Maths Problem

Space

Russian Launch Vehicles Template

Deletion

All FIFA World Cup squad lists

Copa Libertadores de América

CAF Champions League

Champions League Finals

SAM76

Characteristics of the SAM76 language

Notation and Syntax

Weirdo Bug

UEFA Cup

History

2010 FIFA World Cup

Venues

2006 FIFA World Cup

Seeding

European Football Championship

History

Birth of the Competition

New Format introduced

Another Change

Great Political Change

The New Millenia

Format

Qualifying

Groups

Final Tournament

Football in Norway

History

The Football Association of Norway

League system

Cup system

National team

See also

Timelines

Premier League Timeline

FIFA World Rankings Timeline

Elo World Football Timeline

Table

Wiki Timeline

Heysel Stadium disaster

FIFA World Rankings *

History

1999 update

2006 update

Rank leaders

Uses of the rankings

Seeding in the 2006 World Cup

Criticism

How the rankings have changed

The current calculation method

Overview

Win, draw or defeat

Match status

Opposition strength

Regional strength

Confederation weightings

Assesment Period

Summary

Examples

Calculation method from 1999 - 2006

Overview

Winning, drawing or losing

Number of goals

Home and away games

Status of a match

Regional strength factors

Summary

Example 1

Example 2