Wikipedia:Reference desk/Archives/Mathematics/2011 May 13
| Mathematics desk | ||
|---|---|---|
| < May 12 | << Apr | May | Jun >> | May 14 > |
| Welcome to the Wikipedia Mathematics Reference Desk Archives |
|---|
| The page you are currently viewing is an archive page. While you can leave answers for any questions shown below, please ask new questions on one of the current reference desk pages. |
May 13
[edit]Factoring Polynomials
[edit]Err, can someone explain to me how to factor polynomials? I can totally do x^2+bx+c but all of the sudden when I get ax^2+bx+c I just panic and resort to using the quadratic formula. I know there's a faster way to do it, but googling just gives me a whole bunch of stuff I don't understand. Can someone explain a method that's easy to understand?? Thanks! —Preceding unsigned comment added by 142.132.70.60 (talk) 19:21, 13 May 2011 (UTC)
- You can factorize the expression by taking out the 'a' and get . Then you can use your techniques on the term inside the big brackets; but don't forget to put the 'a' back in! HTH, Robinh (talk) 20:53, 13 May 2011 (UTC)
- Personally, I find you have to start with the "x" term in each, for example (x _ _)(3x _ _), if you can fix the signs (if b>0, and c>0, then both signs are positive, if c>0 and b<0, both are negative) and then see if you can get it from there. If there are only a few possible combinations as factors of c then it's possible to write it out. (Also - a small hint, if you can get it in somewhere: if the brackets start with and even number of xs, then the second part of the bracket must be odd, else the whole thing would divide by two and from inspection is can't (unless you missed that originally)) Grandiose (me, talk, contribs) 21:19, 13 May 2011 (UTC)
- The fast way is http://www.wolframalpha.com/input/?i=ax^2%2Bbx%2Bc
- The easy-to-understand way is to check that is equal to Bo Jacoby (talk) 11:35, 15 May 2011 (UTC).
Latex
[edit]Can someone tell me how to draw the following in latex: a hollow square with a diagonal line going from bottom left corner to top right corner, and each line has an arrow head in the middle (not on the ends), so I want the lines to look like their pointing in some direction but I don't want the arrow head on the end points. I need the diagonal line's arrow head pointing 45 degrees clockwise from north. I also need the four vertices labelled as v. If you could post the code I'd appreciate it. Money is tight (talk) 22:32, 13 May 2011 (UTC)
- By far the easiest thing to do is to draw the image in another program, and save it as a .png or .eps or whatever, and use \includegraphics{file}. Invrnc (talk) 23:05, 13 May 2011 (UTC)
- You might try Inkscape to produce a .SVG. SVG is based on XML so if the drawing is simple and you're patient and willing to learn the syntax it's possible to create the file with a text editor.--RDBury (talk) 23:35, 13 May 2011 (UTC)
- Alternatively, there are lots of packages for coding drawings in latex. PGF/TikZ is very good and has an extensive manual with lots of examples (linked from the article). In fact, the standard picture environment is probably enough for what you want to do - there is a nice Wikibooks article with lots of information about picture, that also discusses xy, tikz, xfig, and others. 81.98.38.48 (talk) 14:47, 14 May 2011 (UTC)
- You might try Inkscape to produce a .SVG. SVG is based on XML so if the drawing is simple and you're patient and willing to learn the syntax it's possible to create the file with a text editor.--RDBury (talk) 23:35, 13 May 2011 (UTC)
- Also, in which direction are the other four arrowheads facing? – b_jonas 06:53, 15 May 2011 (UTC)
- The left and right sides of the square are facing upwards, and the top and bottom sides of the square are facing right. Basically I'm trying to draw the triangulation of the torus. Money is tight (talk) 18:54, 15 May 2011 (UTC)
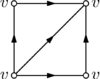
- Here's an example (see thumbnail). See its description page for the EPS (encapsulated Postscript) formatted original that has infinite resolution and you can easily use in a LaTeX article.
- I don't quite understand why you'd want an arrowhead on the diagonal if this is supposed to show the triangulation of the torus. I thought the arrowheads would mean identifying two edges on the drawing. Anyway, for this image I stick to your description so I've put an arrowhead to the diagonal as well, but feel free to modify it in any way you like (including changing the dimensions, font, etc). – b_jonas 21:50, 15 May 2011 (UTC)
- Ah, I get it now. The four vertices are identified, so they should have the same label. I changed the image to have the same label (v) at each vertex. (Still don't get the arrow at the middle.) – b_jonas 21:57, 15 May 2011 (UTC)
- Quoting part of OP's response from my talk page.
- I tried using the scripts you posted but I really don't know how to get them to work (I'm a total computer newbie). There's something more I need about the picture; I need the two vertical edges labelled a, the two horizontal edges labelled b, the diagonal edge labelled c, the top left triangle labelled U, and the bottom right triangle labelled V. Basically I'm trying to get it look like the first of three pictures on page 102 in Hatcher's book (http://www.math.cornell.edu/~hatcher/AT/ATch2.pdf).
- I don't mind your replying on the talk page, and I will probably look at this a bit later, but allow me to copy the reply here as well so other helpful people reading here know about it. – b_jonas 08:37, 17 May 2011 (UTC)
- Quoting part of OP's response from my talk page.
- You don't want to draw a figure, and you have found a good quality figure in an electronically typeset book that matches what you want. Why don't you ask permission to reuse that from the authors of that book? Here's the extracted image (see thumbnail on right). Again, the description page of that image contains the image in EPS (encapsulated Postscript) format, which you can easily include in a LaTeX document compiled with latex+dvips; or convert the image to pdf if you want to compile the LaTeX document with pdflatex. – b_jonas 10:16, 17 May 2011 (UTC)
- Okay, wait a moment. I can't host the figure extracted from the book on the Wikipedia server, for it does not have a free license. So download the extracted figure in EPS format from here. The book comes with the following copyright notice:
- Copyright (c) 2002 by Cambridge University Press. Single paper or electronic copies for noncommercial personal use may be made without explicit permission from the author or publisher. All other rights reserved.
- – b_jonas 16:25, 17 May 2011 (UTC)
Which are Martingales?
[edit]I know that there are two criteria for some to be an -Martingale.
Firstly .
Secondly .
Now is a Wiener process that generates a filtration .
I need to determine whether a couple of functions of are -Martingales or not.
The first one is .
I'm assuming that this passes the first test. Because
As for the second test, I'm guessing that it fails, since
But the second one is much more difficult:
I thought maybe
But I'm guessing there's something wrong about that. As for checking the second condition I really don't know where to begin. Thorstein90 (talk) 00:54, 14 May 2011 (UTC)
- So, the first is not a martingale since it's expectation value is the variance of the Wiener process, which increases with time. The second is a martingale. The condition on the variance is straightforward:
- which you can estimate from above by the Cauchy-Schwarz inequality. For the martingale property, your calculation is basically right, except you need to condition on the initial information . Then
- -Sławomir Biały (talk) 12:20, 16 May 2011 (UTC)
Riemann Hurwitz formula and analytic maps on the Riemann Sphere
[edit]Hello everyone, I'm stuck on the following problem and have no idea how to get going on it, was hoping you could help.
Suppose is an analytic map of degree 2: show that there exist Mobius transformations S, T such that is the square map, .
Now I've just previous to this stated the Riemann Hurwitz formula which applies to f here, and I have also shown that the analytic isomorphisms of the Riemann sphere to itself are the non-constant mobius maps. So, I feel like I must be almost all the way there already, I just need help piecing this together to get the result: any thoughts anyone? Thank you! Totenines99 (talk) 23:59, 13 May 2011 (UTC)
- Take a look at the complex analysis section of the ramification article. Then take a look at the statement section of the article on the Riemann–Hurwitz formula. Notice that you have been asked to consider the map ƒ(z) = z2 which has a ramification of order two, and the Riemann sphere whose Euler characteristic is also two. Finally, the automorphism section of the Möbius transformation article tells us that the automorphisms of the Riemann sphere are the Möbius transformations. — Fly by Night (talk) 01:50, 14 May 2011 (UTC)
- So I see that we can deduce from the formula that my f ramifies at exactly 2 points with multiplicity 2 in each case, right? So are we saying you can map these via T to any other 2 points on the Riemann sphere: do we want these to be 0 and infinity? Even if I have understood that far, I'm not quite following where you go from there, sorry.
- I did have 1 further query while I'm waiting, if anyone can help me with it: I am trying to work out, with the Riemann surface R associated with complete analytic function on and regular covering map , what subgroup of the full symmetric group of is obtained from all closed curves starting and ending at P (since these curves 'lift' to curves between preimages of P under the covering map, each gives a permutation of the preimages of the point P, via the starting/end point of the lifted curve). However, I'm having trouble figuring out how we can actually find out what permutations are possible via these curves: there are 4 preimages to every point under this map, right? (2 from the squaring map and two from the fact that the square root is a multi-valued function) So where do I go from here? I would really be very grateful for your help or advice on both of these problems. Totenines99 (talk) 14:24, 14 May 2011 (UTC)
- No thoughts, anyone? :) Totenines99 (talk) 05:05, 17 May 2011 (UTC)
























