User:YachnaZiyangMichael/sandbox
Origami-Constructible Numbers
[edit]Origami is studied in the context of algebra and complex numbers. It is the art of paper folding, originating in Japan during the 17th century AD. Areas of interest include the use of paper folds to solve mathematical equations and a given paper model's flat-foldability (to see if the model can be flattened without ruining it).[1] In an origami construction, we start with a sheet of paper that we can consider to be infinitely large. The sheet of paper represents the complex plane and also has two points marked on it: 0 and 1. The real axis goes through both of these points and the imaginary axis is perpendicular to the real axis, intersecting it at the point 0. Thus, we can discuss points and complex numbers interchangeably.
Origami constructions consist of a series of folds in the paper. When the paper is folded and unfolded, it leaves a crease which, in our constructions, acts as a line. In our origami constructions, a point only exists if it lies at the intersection of two creases. The types of folds we can do, all of which are straight lines, are defined by the Huzita-Hatori axioms. A complex number is origami-constructible if, starting with a sheet of paper with 0 and 1 marked, we can make a series of folds such that two of the lines intersect at a point p that corresponds to ’s position on the complex plane.[2]
History
[edit]To add some context to our discussion, we will delve into the history of origami in a mathematical setting. Despite origami's deep roots in Japanese culture as a paper folding art, it was in fact, an Indian, T. Sundara Rao, who was the first to use it in a mathematical context. In 1893, he and Addison & co. published Geometric Exercises in Paper Folding[3]. The key idea in relation to origami, was that it could be used in the trisection of angles. There were also heavily implications that there was no way to construct a cube root using origami.
However, in 1936, Italian mathematician, Margherita Piazzola Beloch, proved that there was a way to use origami to construct a cube root. She used the so called "Beloch fold" (used in the Huzita–Hatori axioms below), to allow the general cubic equation to be solved using origami.
There were further developments in the Huzita-Hatori axioms, made Jacques Justin in 1986 and expanded upon by Humiaki Huzita in 1991, respectively. In 1996, an American physicist, Robert J. Lang published the proof of the completeness of the Huzita–Hatori axioms[4].
Lang also made strides in the field of computational origami. In 1990, Lang produced the first version of the TreeMaker program; which was able to convert a line drawing into a for a paper base from which a model could be folded. By 1998, TreeMaker was able to construct the full crease pattern for a plethora of origami bases.[5]
Euclidean Constructions
[edit]Constructions come from a need to create certain objects in our proofs. In Greek times, geometric constructions of lengths and figures were restricted to the use of a straightedge and compass. No markings could be placed on the straightedge to be used to make measurements. [6]
These constructions are sometimes also known as Euclidean constructions due to the important place Greek geometric constructions held in Euclid’s Elements. Such constructions lay at the heart of the three classical geometric problems (1) squaring the circle (2) duplicating the cube, and (3) trisecting an arbitrary angle. The Greeks could not solve these problems. It took until the eighteenth and nineteenth century to prove that these problems were impossible under the restraints imposed.
The constructions are all related to Euclid’s first three axioms:
1. To draw a straight line from any point to any point.
2. To produce a finite straight line continuously in a straight line.
3. To draw a circle with any centre and radius.
The Huzita–Hatori axioms
[edit]The Huzita–Hatori axioms are a set of rules related to the mathematical principles of paper folding, describing the operations that can be made when folding a piece of paper. The axioms assume that the operations are completed on a plane and that all folds are linear. The axioms were first discovered by Jacques Justin in 1986. Axioms 1 through 6 were rediscovered by Japanese-Italian mathematician Humiaki Huzita and reported at the First International Conference on Origami in Education and Therapy in 1991. Axioms 1 though 5 were rediscovered by Auckly and Cleveland in 1995. Axiom 7 was rediscovered by Koshiro Hatori in 2001; Robert J. Lang also found axiom 7.[7]
Axiom 1:Given two distinct points p1 and p2, there is a unique fold that passes through both of them.
[edit]
In parametric form, the equation for the line that passes through the two points is :
Axiom 2:Given two points p1 and p2, there is a unique fold that places p1 onto p2.
[edit]
This is equivalent to finding the perpendicular bisector of the line segment p1p2. This can be done in four steps:
- Use Axiom 1 to find the line through p1 and p2, given by
- Find the midpoint of pmid of P(s)
- Find the vector vperp perpendicular to P(s)
- The parametric equation of the fold is then:
Axiom 3:Given two lines l1 and l2, there is a fold that places l1 onto l2。
[edit]
This is equivalent to finding a bisector of the angle between l1 and l2. Let p1 and p2 be any two points on l1, and let q1 and q2 be any two points on l2. Also, let u and v be the unit direction vectors of l1 and l2, respectively; that is:
If the two lines are not parallel, their point of intersection is:
where
The direction of one of the bisectors is then:
And the parametric equation of the fold is:
A second bisector also exists, perpendicular to the first and passing through pint. Folding along this second bisector will also achieve the desired result of placing l1 onto l2. It may not be possible to perform one or the other of these folds, depending on the location of the intersection point.
If the two lines are parallel, they have no point of intersection. The fold must be the line midway between l1 and l2 and parallel to them.
Axiom 4:Given a point p1 and a line l1, there is a unique fold perpendicular to l1 that passes through point p1.
[edit]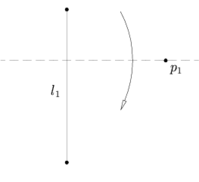
This is equivalent to finding a perpendicular to that passes through . If we work out a vector that is perpendicular to the line , the parametric equation of the fold will be:
Axiom 5:Given two points p1 and p2 and a line l1, there is a fold that places p1 onto l1 and passes through p2.
[edit]
This is equivalent to finding the intersection of a line with a circle. This means that it may have 0, 1, or 2 solutions. The line is defined by , and the circle has its centre at , and a radius equal to the distance between and . If the line does not meet the circle at any point, there are no solutions. If the line is tangent to the circle, there is one solution, and if the line intersects the circle in two places, there are two solutions.
If we know two points on the line, (x1, y1) and (x2, y2), then the line can be expressed parametrically as:
Let the circle be defined by its center at p2=(xc, yc), with radius . Then the circle can be expressed as:
In order to determine the points of intersection of the line with the circle, we substitute the x and y components of the equations for the line into the equation for the circle, giving:
Or, simplified:
where:
Then we simply solve the quadratic equation:
If the discriminant b2 − 4ac < 0, there are no solutions. The circle does not intersect or touch the line. If the discriminant is equal to 0, then there is a single solution, where the line is tangent to the circle. And if the discriminant is greater than 0, there are two solutions, representing the two points of intersection. Let us call the solutions d1 and d2, if they exist. We have 0, 1, or 2 line segments:
A fold F1(s) perpendicular to m1 through its midpoint will place p1 on the line at location d1. Similarly, a fold F2(s) perpendicular to m2 through its midpoint will place p1 on the line at location d2. The application of Axiom 2 easily accomplishes this. The parametric equations of the folds are thus:
Axiom 6:Given two points p1 and p2 and two lines l1 and l2, there is a fold that places p1 onto l1 and p2 onto l2.
[edit]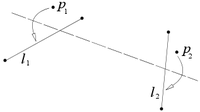
This is equivalent to finding a line simultaneously tangent to two parabolas, and can be considered equivalent to solving a third-degree equation as there are in general three solutions. The two parabolas have foci at and , respectively, with directrices (lines used to define a curve or surface defined) by and , respectively. This fold is called the Beloch fold after Margharita P. Beloch, who in 1936 showed using it that origami can be used to solve general cubic equations.[8]
Axiom 7:Given one point p and two lines l1 and l2, there is a fold that places p onto l1 and is perpendicular to l2.
[edit]
We have seen that Axiom 5 can have 0, 1, or 2 solutions and Axiom 6 can have 0, 1, 2, or 3 solutions. Because of this, the geometries of origami are considered stronger than the geometries of straight-edge and compass, where the maximum number of solutions an axiom can have is 2. Thus, compass and straightedge geometry solves second-degree equations, while so-called origami geometry, can solve third-degree equations, and solve problems such as angle trisection and doubling of the cube. It is worth noting, though, that the construction of the fold by Axiom 6 requires the "sliding" of the paper, which is not allowed in classical straight-edge and compass constructions.[7]
Field operations
[edit]The field of all origami-constructible numbers forms a subfield of the field Complex numbers, . For all and that exist within the field then and also exist and exists if .[7]
Elementary Operations
[edit]There are two elementary operations that are combinations of multiple axioms that help us to form create the more well known operations of addition, multiplication and inversion.
E1. Given a point and a line , fold a line parallel to that goes through .
This can be done by two uses of A4. The first to construct a line through perpendicular to and the second to create a new line through perpendicular to the first line created and hence parallel to the original line.
E2. Given a point and a line , reflect across .
This can be done by using A4 to construct a line through perpendicular to . Then by picking a point on that is not on the new create line (such a point an be created by the intersection of and a line passing through 0 or 1). Now using A5 on this new point, and the new line to fold across and mark the line going through and the new created point. This marks the new point which is the reflection of across .
Multiplication
[edit]To Multiply by a real number can be done by using A1 on points 0 and and on 1 and to create two new lines, and respectively. Then by applying E1 to and the number to multiply by This will create a new line that will intersect at the point .
To multiply by we use A1 on 0 and to create line then use A4 on 0 and to create line then use A2 on and to create line . Finally using E2 on and will create the point .
Addition
[edit]Addition can be performed using E1 and A1. starting with the two points to be added: and and the point 0 then use A1 to create lines through and 0 and and 0. Then by using E1 twice to find the lines parallel to these lines that pass through the other point. This will create a parallelogram with points and a forth point. this forth point is the addition of and .
This method only works if , and 0 are not all on the same line. If this is the case a new method must be used. Using A1 to create a line through all three points and using A2 to fold onto so a new point lies over 0. Using A4 on 0 and the line with the paper still folded creates a new point This will mark , the sum of the two points.
Inversion
[edit]The process to invert a number is very similar to multiplication. To start with two lines can be made using A1 on and 0 and A1 on and Then a third line is made using E1 on 1 and the second created line. This line intersecting with the first will mark the inverse.
This can be done for complex numbers in the same manner as multiplication.
Other Constructions
[edit]Doubling the Cube
[edit]Doubling the cube can be done in origami by creating the length . This can be done by taking a piece of square paper and folding it into 3 equal horizontal strips. A bottom corner is then moved onto the top edge where the mark at at the intersection of the bottom edge and one of the fold creases is place directly over the other crease. The point now marked at the top edge will be times further from one corner than the other.[9]
Trisecting the Angle
[edit]Trisecting the angle can also be done by creating two parallel folds and with the distances to and to a edge of the angle being equal and the angle is on the bottom left corner. The left edge of the fold is the placed over the other edge of the angle with the bottom left corner being placed on the fold . The points marked by the new positions of the bottom left corner and the left edge of can then be used to trisect the angle by creating folds between them and the angle.[9]
Solving Polynomials
[edit]There are a few methods for solving polynomials using origami. A method of solving cubic equations such as is to construct the points and and the lines and . Using Axiom 6 will create a new line where is the solution to the original equation.
This method can also be used to find cube roots by solving the equation .
A method of solving polynomials to any degree called Lill's Method was adapted to solve cubic equations in origami by Margharita P. Beloch. This method uses connecting line segments with lengths of the coefficients of the polynomial and lines at certain to find lengths equal to the roots of the polynomial. This method can be used to find the roots of polynomials of any degree using origami if simultaneous folds are allowed.
Power of Origami and Neusis
[edit]The advantage origami techniques have over regular compass and straight edge constructions comes from the ability to use Neusis construction as a method of solving problems. Neusis construction consists of fitting a line element of given length in between two given lines (and ), in such a way that the line element, or its extension, passes through a given point . That is, one end of the line element has to lie on , the other end on , while the line element is "inclined" towards P. This extra ability is the reason for all constructions available to origami, and not otherwise, including the neusis construction. This allows the construction of a common tangent line of two parabolas, trisecting angles, doubling the cube and many other constructions.
Other constructible numbers
[edit]Negative numbers can be constructed. Negating a number is equivalent to reflecting it across 0. We can do this using A1, A4 and E2 in order. Square and cube roots are also constructible. Square roots can be constructed by using circle geometry to create a point where a circle centred at with radius intersects the real axis at point . Cube roots can be solved by solving cubic equations as mentioned above.
Another origami-constructibe number is assuming that itself if constructible. This can be constructed as a right angle triangle with 1 and as the sides of the triangle and as the hypotenuse.[10]
Any sided regular polygon is constructible if and only if where and are distinct primes of the form .[7]
Related Problems
[edit]There are many other problems that origami can be used to solve. They include:
- The modular origami technique uses two or more sheets of paper to create more complex structures, which would be impossible using a single sheet of paper. This is often used to model three-dimensional shapes such as an icosahedron.
- Sonobe is a type of modular origami, which can be used to construct a plethora of shapes, from cubes to deltahedrons.[11]
- The Miura fold is a type of rigid origami in which one can fold a flat surface into a smaller area. This property has allowed it to be used for large solar panel arrays for space satellites[12] and utilised by researchers to stack hydrogel films, generating electricity in a way similar to electric eels.[13]
- In terms of user accessibility, the method of pureland origami adds the restrictions that only simple mountain/valley folds may be used, and all folds must have straightforward locations. This allows beginners and those with impaired motor skills to access origami as well.
Notes and references
[edit]- ^ "Mathematics of paper folding", Wikipedia, 2020-02-03, retrieved 2020-03-18
- ^ "Origami-Constructible Numbers, James King" (PDF). S2CID 16022323.
{{cite web}}: CS1 maint: url-status (link) - ^ "Geometric Exercises in Paper Folding".
- ^ "Robert Lang - Origami Constructions" (PDF).
- ^ "Computational Origami".
- ^ "Euclidean Constructions" (PDF).
{{cite web}}: CS1 maint: url-status (link) - ^ Jump up to: a b c d "Huzita–Hatori_axioms".
{{cite web}}: CS1 maint: url-status (link) - ^ Hull, Thomas C. (April 2011). ""Solving Cubics With Creases: The Work of Beloch and Lill"" (PDF).
- ^ Jump up to: a b Oller, Antonio M. (2007). "Origami constructions". arXiv:0709.3270.
- ^ https://sites.math.washington.edu/~morrow/336_09/papers/Sheri.pdf
- ^ "Sonobe".
- ^ "Mathematics and technical origami".
- ^ "Muira fold".




























![{\displaystyle {\begin{aligned}F_{1}(s)&=p_{1}+{\frac {1}{2}}(d_{1}-p_{1})+s(d_{1}-p_{1})^{\perp }\\[8pt]F_{2}(s)&=p_{1}+{\frac {1}{2}}(d_{2}-p_{1})+s(d_{2}-p_{1})^{\perp }.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a48e70d1a14331f3013f2e5a17da2fd2f29c28d6)
















![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)



















