Example 1

Example (45 voters; 5 candidates):

5 ACBED (that is, 5 voters have order of preference: A > C > B > E > D)

5 ADECB

8 BEDAC

3 CABED

7 CAEBD

2 CBADE

7 DCEBA

8 EBADC

The matrix of pairwise defeats looks as follows:
	d[*,A]	d[*,B]	d[*,C]	d[*,D]	d[*,E]
d[A,*]		20	26	30	22
d[B,*]	25		16	33	18
d[C,*]	19	29		17	24
d[D,*]	15	12	28		14
d[E,*]	23	27	21	31

The graph of pairwise defeats looks as follows:

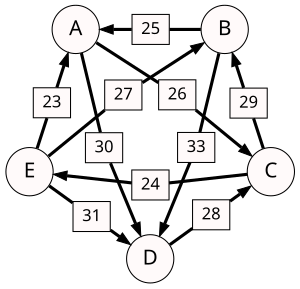
The strength of a path is the strength of its weakest link. For each pair of candidates X and Y, the following table lists the strongest path from candidate X to candidate Y. The critical defeats of the strongest paths are underlined.

The strongest paths are:
	... to A	... to B	... to C	... to D	... to E
from A ...		A-(30)-D-(28)-C-(29)-B	A-(30)-D-(28)-C	A-(30)-D	A-(30)-D-(28)-C-(24)-E	from A ...
from B ...	B-(25)-A		B-(33)-D-(28)-C	B-(33)-D	B-(33)-D-(28)-C-(24)-E	from B ...
from C ...	C-(29)-B-(25)-A	C-(29)-B		C-(29)-B-(33)-D	C-(24)-E	from C ...
from D ...	D-(28)-C-(29)-B-(25)-A	D-(28)-C-(29)-B	D-(28)-C		D-(28)-C-(24)-E	from D ...
from E ...	E-(31)-D-(28)-C-(29)-B-(25)-A	E-(31)-D-(28)-C-(29)-B	E-(31)-D-(28)-C	E-(31)-D		from E ...
	... to A	... to B	... to C	... to D	... to E

The strengths of the strongest paths are:
	p[*,A]	p[*,B]	p[*,C]	p[*,D]	p[*,E]
p[A,*]		28	28	30	24
p[B,*]	25		28	33	24
p[C,*]	25	29		29	24
p[D,*]	25	28	28		24
p[E,*]	25	28	28	31

Candidate E is a potential winner, because p[E,X] ≥ p[X,E] for every other candidate X.

As 25 = p[E,A] > p[A,E] = 24, candidate E is better than candidate A.

As 28 = p[E,B] > p[B,E] = 24, candidate E is better than candidate B.

As 28 = p[E,C] > p[C,E] = 24, candidate E is better than candidate C.

As 31 = p[E,D] > p[D,E] = 24, candidate E is better than candidate D.

As 28 = p[A,B] > p[B,A] = 25, candidate A is better than candidate B.

As 28 = p[A,C] > p[C,A] = 25, candidate A is better than candidate C.

As 30 = p[A,D] > p[D,A] = 25, candidate A is better than candidate D.

As 29 = p[C,B] > p[B,C] = 28, candidate C is better than candidate B.

As 29 = p[C,D] > p[D,C] = 28, candidate C is better than candidate D.

As 33 = p[B,D] > p[D,B] = 28, candidate B is better than candidate D.

Therefore, the Schulze ranking is E > A > C > B > D.

Example 2

Example (30 voters; 4 candidates):

5 ACBD

2 ACDB

3 ADCB

4 BACD

3 CBDA

3 CDBA

1 DACB

5 DBAC

4 DCBA

The matrix of pairwise defeats looks as follows:
	d[*,A]	d[*,B]	d[*,C]	d[*,D]
d[A,*]		11	20	14
d[B,*]	19		9	12
d[C,*]	10	21		17
d[D,*]	16	18	13

The graph of pairwise defeats looks as follows:

The strength of a path is the strength of its weakest link. For each pair of candidates X and Y, the following table lists the strongest path from candidate X to candidate Y. The critical defeats of the strongest paths are underlined.

The strongest paths are:
	... to A	... to B	... to C	... to D
from A ...		A-(20)-C-(21)-B	A-(20)-C	A-(20)-C-(17)-D	from A ...
from B ...	B-(19)-A		B-(19)-A-(20)-C	B-(19)-A-(20)-C-(17)-D	from B ...
from C ...	C-(21)-B-(19)-A	C-(21)-B		C-(17)-D	from C ...
from D ...	D-(18)-B-(19)-A	D-(18)-B	D-(18)-B-(19)-A-(20)-C		from D ...
	... to A	... to B	... to C	... to D

The strengths of the strongest paths are:
	p[*,A]	p[*,B]	p[*,C]	p[*,D]
p[A,*]		20	20	17
p[B,*]	19		19	17
p[C,*]	19	21		17
p[D,*]	18	18	18

Candidate D is a potential winner, because p[D,X] ≥ p[X,D] for every other candidate X.

As 18 = p[D,A] > p[A,D] = 17, candidate D is better than candidate A.

As 18 = p[D,B] > p[B,D] = 17, candidate D is better than candidate B.

As 18 = p[D,C] > p[C,D] = 17, candidate D is better than candidate C.

As 20 = p[A,B] > p[B,A] = 19, candidate A is better than candidate B.

As 20 = p[A,C] > p[C,A] = 19, candidate A is better than candidate C.

As 21 = p[C,B] > p[B,C] = 19, candidate C is better than candidate B.

Therefore, the Schulze ranking is D > A > C > B.

Example 3

Example (30 voters; 5 candidates):

3 ABDEC

5 ADEBC

1 ADECB

2 BADEC

2 BDECA

4 CABDE

6 CBADE

2 DBECA

5 DECAB

The matrix of pairwise defeats looks as follows:
	d[*,A]	d[*,B]	d[*,C]	d[*,D]	d[*,E]
d[A,*]		18	11	21	21
d[B,*]	12		14	17	19
d[C,*]	19	16		10	10
d[D,*]	9	13	20		30
d[E,*]	9	11	20	0

The graph of pairwise defeats looks as follows:

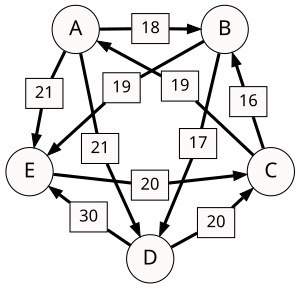
The strength of a path is the strength of its weakest link. For each pair of candidates X and Y, the following table lists the strongest path from candidate X to candidate Y. The critical defeats of the strongest paths are underlined.

The strongest paths are:
	... to A	... to B	... to C	... to D	... to E
from A ...		A-(18)-B	A-(21)-D-(20)-C	A-(21)-D	A-(21)-E	from A ...
from B ...	B-(19)-E-(20)-C-(19)-A		B-(19)-E-(20)-C	B-(19)-E-(20)-C-(19)-A-(21)-D	B-(19)-E	from B ...
from C ...	C-(19)-A	C-(19)-A-(18)-B		C-(19)-A-(21)-D	C-(19)-A-(21)-E	from C ...
from D ...	D-(20)-C-(19)-A	D-(20)-C-(19)-A-(18)-B	D-(20)-C		D-(30)-E	from D ...
from E ...	E-(20)-C-(19)-A	E-(20)-C-(19)-A-(18)-B	E-(20)-C	E-(20)-C-(19)-A-(21)-D		from E ...
	... to A	... to B	... to C	... to D	... to E

The strengths of the strongest paths are:
	p[*,A]	p[*,B]	p[*,C]	p[*,D]	p[*,E]
p[A,*]		18	20	21	21
p[B,*]	19		19	19	19
p[C,*]	19	18		19	19
p[D,*]	19	18	20		30
p[E,*]	19	18	20	19

Candidate B is a potential winner, because p[B,X] ≥ p[X,B] for every other candidate X.

As 19 = p[B,A] > p[A,B] = 18, candidate B is better than candidate A.

As 19 = p[B,C] > p[C,B] = 18, candidate B is better than candidate C.

As 19 = p[B,D] > p[D,B] = 18, candidate B is better than candidate D.

As 19 = p[B,E] > p[E,B] = 18, candidate B is better than candidate E.

As 20 = p[A,C] > p[C,A] = 19, candidate A is better than candidate C.

As 21 = p[A,D] > p[D,A] = 19, candidate A is better than candidate D.

As 21 = p[A,E] > p[E,A] = 19, candidate A is better than candidate E.

As 20 = p[D,C] > p[C,D] = 19, candidate D is better than candidate C.

As 30 = p[D,E] > p[E,D] = 19, candidate D is better than candidate E.

As 20 = p[E,C] > p[C,E] = 19, candidate E is better than candidate C.

Therefore, the Schulze ranking is B > A > D > E > C.

Example 4

Example (9 voters; 4 candidates):

3 ABCD

2 DABC

2 DBCA

2 CBDA

The matrix of pairwise defeats looks as follows:
	d[*,A]	d[*,B]	d[*,C]	d[*,D]
d[A,*]		5	5	3
d[B,*]	4		7	5
d[C,*]	4	2		5
d[D,*]	6	4	4

The graph of pairwise defeats looks as follows:

The strength of a path is the strength of its weakest link. For each pair of candidates X and Y, the following table lists the strongest path from candidate X to candidate Y. The critical defeats of the strongest paths are underlined.

The strongest paths are:
	... to A	... to B	... to C	... to D
from A ...		A-(5)-B	A-(5)-C	A-(5)-C-(5)-D	from A ...
from B ...	B-(5)-D-(6)-A		B-(7)-C	B-(5)-D	from B ...
from C ...	C-(5)-D-(6)-A	C-(5)-D-(6)-A-(5)-B		C-(5)-D	from C ...
from D ...	D-(6)-A	D-(6)-A-(5)-B	D-(6)-A-(5)-C		from D ...
	... to A	... to B	... to C	... to D

The strengths of the strongest paths are:
	p[*,A]	p[*,B]	p[*,C]	p[*,D]
p[A,*]		5	5	5
p[B,*]	5		7	5
p[C,*]	5	5		5
p[D,*]	6	5	5

Candidate B and candidate D are potential winners, because p[B,X] ≥ p[X,B] for every other candidate X and p[D,Y] ≥ p[Y,D] for every other candidate Y.

As 7 = p[B,C] > p[C,B] = 5, candidate B is better than candidate C.

As 6 = p[D,A] > p[A,D] = 5, candidate D is better than candidate A.

Possible Schulze rankings are B > C > D > A, B > D > A > C, B > D > C > A, D > A > B > C, D > B > A > C, and D > B > C > A.