User:JosefL123/sandbox

The graph (bottom, in red) of the signed distance between a fixed disk (top, in grey) and a point of the plane containing the disk (the xy plane, shown in blue)

A more complicated set (top) and the graph of its signed distance function (bottom, in red).

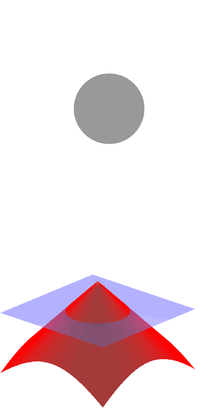
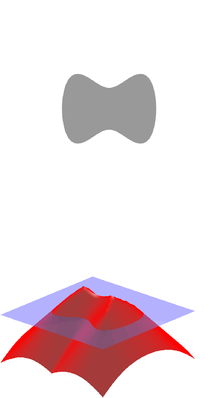
In mathematics and its applications, the signed distance function (or oriented distance function) of a set Ω in a metric space determines the distance of a given point x from the boundary of Ω, with the sign determined by whether x is in Ω. The function has positive values at points x inside Ω, it decreases in value as x approaches the boundary of Ω where the signed distance function is zero, and it takes negative values outside of Ω. However, the alternative convention is also sometimes taken instead (i.e., negative inside Ω and positive outside).

Definition

If Ω is a subset of a metric space X with metric d, then the signed distance function f is defined by

$f(x)={\begin{cases}d(x,\partial \Omega )&{\mbox{if }}\,x\in \Omega \\-d(x,\partial \Omega )&{\mbox{if }}\,x\in \Omega ^{c}\end{cases}}$

where $\partial \Omega$ denotes the boundary of $\Omega$. For any $x\in X$,

$d(x,\partial \Omega ):=\inf _{y\in \partial \Omega }d(x,y)$

where inf denotes the infimum.

Properties in Euclidean space

If Ω is a subset of the Euclidean space Rⁿ with piecewise smooth boundary, then the signed distance function is differentiable almost everywhere, and its gradient satisfies the eikonal equation

$|\nabla f|=1.$

If the boundary of Ω is C^k for k ≥ 2 (see Differentiability classes) then d is C^k on points sufficiently close to the boundary of Ω. In particular, on the boundary f satisfies

$\nabla f(x)=N(x),$

where N is the inward normal vector field. The signed distance function is thus a differentiable extension of the normal vector field. In particular, the Hessian of the signed distance function on the boundary of Ω gives the Weingarten map.

If, further, Γ is a region sufficiently close to the boundary of Ω that f is twice continuously differentiable on it, then there is an explicit formula involving the Weingarten map W_x for the Jacobian of changing variables in terms of the signed distance function and nearest boundary point. Specifically, if T(∂Ω, μ) is the set of points within distance μ of the boundary of Ω (i.e. the tubular neighbourhood of radius μ), and g is an absolutely integrable function on Γ, then

$\int _{T(\partial \Omega ,\mu )}g(x)\,dx=\int _{\partial \Omega }\int _{-\mu }^{\mu }g(u+\lambda N(u))\,\det(I-\lambda W_{u})\,d\lambda \,dS_{u},$

where det denotes the determinant and dS_u indicates that we are taking the surface integral.

Algorithms

Algorithms for calculating the signed distance function include the efficient fast marching method, fast sweeping method and the more general level-set method.

For voxel rendering, a fast algorithm for calculating the SDF in taxicab geometry uses summed-area tables.

Applications

Signed distance fields stored as raster images can be used to represent shapes.

Signed distance functions are applied, for example, in real-time rendering, for instance the method of SDF ray marching, and computer vision.

A modified version of SDF was introduced as a loss function to minimize the error in interpenetration of pixels while rendering multiple objects. In particular, for any pixel that does not belong to an object, if it lies outside the object in rendition, no penalty is imposed; if it does, a positive value proportional to its distance inside the object is imposed.

$f(x)={\begin{cases}0&{\text{if }}\,x\in \Omega ^{c}\\d(x,\partial \Omega )&{\text{if }}\,x\in \Omega \end{cases}}$

They have also been used in a method (advanced by Valve) to render smooth fonts at large sizes (or alternatively at high DPI) using GPU acceleration. Valve's method computed signed distance fields in raster space in order to avoid the computational complexity of solving the problem in the (continuous) vector space. More recently piece-wise approximation solutions have been proposed (which for example approximate a Bézier with arc splines), but even this way the computation can be too slow for real-time rendering, and it has to be assisted by grid-based discretization techniques to approximate (and cull from the computation) the distance to points that are too far away.

In Computer Graphics

Any shape that can have a SDF defined for it can be rendered by a computer. Primitive shapes such as spheres, boxes, and line segments are some examples of things that can be rendered from these SDFs. Rounding of shapes can be done by simply subtracting a value from the final signed distance value of a form. They can also be hallowed out by taking the absolute value of the distance and subtracting a value that specifies the thickness of the shape.

These primitive shapes can be combined using Boolean operations such as union, intersection and difference to define more complex forms within a scene. Taking the minimum of two SDFs will result in union of the 2 shapes. Intersection of the 2 SDFs can be created from taking the maximum. While these Boolean operations are the simplest way to combine SDFs, any function can be used to define how the distances are calculated. For example, by taking a soft minimum shapes can be combined in a way that creates a smooth translation between them.

Translation, scaling, and rotations of SDFs can be completed by applying a translation matrix to the distance field. Deformations and distortions can be applied to SDFs as well by moving it out of non-Euclidean space. When ray marching after apply these operations, it may be necessary to take smaller steps.

These SDF formulas are a useful tool for rendering 3D fractals. Using the modulo operation to define the equation of a distance field, geometry can be repeated indefinitely. Using this technique, fractals can be rendered at a far faster rate then by other methods. Further more, applying rotational and translational operations allows for more complex geometry, and since and since SDF are not limited by resolution, detailed fractal geometry can be created. Finite repetition can also be achieved by clamping the coordinate of points within a fixed range.

In Game Engines

The game engine Unreal Engine makes use of signed distance fields to handle everything from shadow generation to ambient occlusion. Creates these signed distance fields as volumes that store the distance to the nearest surface at each point within the volume. This allows Unreal Engine to leverage ray marching in-order to do real time rendering. It also allows for an approximate cone intersection to be calculated, which can allow for softer shadows and sky occlusion.

In 2020, the FOSS game engine Godot 4.0 received SDF-based real-time global illumination (SDFGI), that became a compromise between more realistic voxel-based GI and baked GI. Its core advantage is that it can be applied to infinite space, which allows developers to use it for open-world games.

In Computer Vision

Object reconstruction is a operation that often needs to be completed when SDFs provide a more robust representation for object reconstruction compared to other methods, such as voxels, point cloud, and mesh based representations. DeepSDF is a methods that uses a neural network encodes a class of SDFs to produce shape representations, interpolations, and completion. A decoder network is used to translate a latent space representation of an SDF into the SDF itself. This allows for a smooth transition between SDFs as the latent vector is changed. Through the process of backpropagation, partial reconstruction data, such as from a point cloud, can be used to extract an SDF.

See also

• Distance function
• Level-set method
• Eikonal equation
• Parallel (aka offset) curve

References

• Stanley J. Osher and Ronald P. Fedkiw (2003). Level Set Methods and Dynamic Implicit Surfaces. Springer. ISBN 9780387227467.
• Gilbarg, D.; Trudinger, N. S. (1983). Elliptic Partial Differential Equations of Second Order. Grundlehren der mathematischen Wissenschaften. Vol. 224 (2nd ed.). Springer-Verlag. (or the Appendix of the 1977 1st ed.)

Category:Applied mathematics Category:Distance