User:Jgmoxness/sandbox

This is the user sandbox of Jgmoxness. A user sandbox is a subpage of the user's user page. It serves as a testing spot and page development space for the user and is not an encyclopedia article. Create or edit your own sandbox here.

Other sandboxes: Main sandbox | Template sandbox

Finished writing a draft article? Are you ready to request review of it by an experienced editor for possible inclusion in Wikipedia? Submit your draft for review!

The Fano plane shown above with $e_{n}$ and IJKL multiplication matrices also includes the geometric algebra basis with signature $(- - - -)$ and is given in terms of the following 7 quaternionic triples (omitting the scalar identity element):

(I, j, k) , (i, J, k) , (i, j, K) , (I, J, K) , (★ I, i, l) , (★ J, j, l), (★ K, k, l)

or alternatively:

(\sigma _{1},j,k),(i,\sigma _{2},k),(i,j,\sigma _{3}),(\sigma _{1},\sigma _{2},\sigma _{3}),

in which the lower case items {i, j, k, l} are vectors (e.g. { $\gamma _{0},\gamma _{1},\gamma _{2},\gamma _{3}$ }, respectively) and the upper case ones {I,J,K}={σ₁,σ₂,σ₃} are bivectors (e.g. $\gamma _{\{1,2,3\}}\gamma _{0}$ , respectively) and the Hodge star operator $★ = i j k l$ is the pseudo-scalar element. If the $★$ is forced to be equal to the identity, then the multiplication ceases to be associative, but the $★$ may be removed from the multiplication table resulting in an octonion multiplication table.

In keeping $★ = i j k l$ associative and thus not reducing the 4 dimensional geometric algebra to an octonion one, the whole multiplication table can be derived from the equation for $★$ . Consider the gamma matrices in the examples given above. The formula defining the fifth gamma matrix ( $\gamma _{5}$ ) shows that it is the $★$ of a four-dimensional geometric algebra of the gamma matrices.

STA's even-graded elements (scalars, bivectors, pseudoscalar) form a Clifford Cl_3,0(R) even subalgebra equivalent to the APS or Pauli algebra.^[1]^: 12 The STA bivectors are equivalent to the APS vectors and pseudovectors. The STA subalgebra becomes more explicit by renaming the STA bivectors ${\textstyle (\gamma _{1}\gamma _{0},\gamma _{2}\gamma _{0},\gamma _{3}\gamma _{0})}$ as ${\textstyle (\sigma _{1},\sigma _{2},\sigma _{3})}$ and the STA bivectors ${\textstyle (\gamma _{3}\gamma _{2},\gamma _{1}\gamma _{3},\gamma _{2}\gamma _{1})}$ as ${\textstyle (I\sigma _{1},I\sigma _{2},I\sigma _{3})}$ .^[1]^: 22^[2]^: 37 The Pauli matrices, ${\textstyle {\hat {\sigma }}_{1},{\hat {\sigma }}_{2},{\hat {\sigma }}_{3}}$ , are a matrix representation for ${\textstyle \sigma _{1},\sigma _{2},\sigma _{3}}$ .^[2]^: 37 For any pair of ${\textstyle (\sigma _{1},\sigma _{2},\sigma _{3})}$ , the nonzero inner products are ${\textstyle \sigma _{1}\cdot \sigma _{1}=\sigma _{2}\cdot \sigma _{2}=\sigma _{3}\cdot \sigma _{3}=1}$ , and the nonzero outer products are:^[2]^: 37^[1]^: 16

{\begin{aligned}\sigma _{1}\wedge \sigma _{2}&=I\sigma _{3}\\\sigma _{2}\wedge \sigma _{3}&=I\sigma _{1}\\\sigma _{3}\wedge \sigma _{1}&=I\sigma _{2}\\\end{aligned}}

The sequence of algebra to even subalgebra continues as algebra of physical space, quaternion algebra, complex numbers and real numbers. The even STA subalgebra Cl⁺(1,3) of real space-time spinors in Cl(1,3) is isomorphic to the Clifford geometric algebra Cl(3,0) of Euclidean space R³ with basis elements. See the illustration of space-time algebra spinors in Cl⁺(1,3) under the octonionic product as a Fano plane. ^[3]

Dual Snub 24-cell
Orthogonal projection
Type	4-polytope
Cells	96
Faces	432	144 kites 288 Isosceles triangle
Edges	480
Vertices	144
Dual	Snub_24-cell
Properties	convex

In geometry, the dual Snub_24-cell is a convex uniform 4-polytope composed of 96 regular cells. Each cell has faces of two kinds: 3 kites and 6 isosceles triangles. The polytope has a total of 432 faces (144 kites and 288 isosceles triangles) and 480 edges.

3D Visualization of the hull of the dual snub 24-Cell, with vertices colored by overlap count:
The (42) yellow have no overlaps.
The (51) orange have 2 overlaps.
The (18) tetrahedral hull surfaces are uniquely colored.

Semiregular polytope

It was discovered by Koca et al. in a 2011 paper.^[4]

Coordinates

The vertices of a dual snub 24-cell are obtained through non-commutative multiplication of the simple roots (T') used in the quaternion base generation of the 600 vertices of the 120-cell. The following orbits of weights of D4 under the Weyl group W(D4):

O(0100) : T = {±1,±e1,±e2,±e3,(±1±e1±e2±e3)/2}

O(1000) : V1

O(0010) : V2

O(0001) : V3

Constructions

One can build it from the subsets of the 120-cell, namely the 24 vertices of T=24-cell, 24 vertices of the alternate T'=D₄ 24-cell, and 96 vertices of the alternate snub 24-cell S'=T'^n=1-4 using the quaternion construction of the 120-cell and non-commutative multiplication.

2D Orthogonal projection
Dual Snub 24-cell
2D projection of the dual snub 24-cell with color coded vertex overlaps.

Dual

The dual polytope of this polytope is the Snub 24-cell.

Notes

^ ^a ^b ^c Hestenes 2015.
^ ^a ^b ^c Doran & Lasenby 2003.
^ Lasenby 2022.
^ Koca, Al-Ajmi & Koca 2011.

References

T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
H. S. M. Coxeter (1973). Regular Polytopes. New York: Dover Publications Inc. pp. 151–152, 156–157.
Snub icositetrachoron - Data and images
3. Convex uniform polychora based on the icositetrachoron (24-cell) - Model 31, George Olshevsky.
Klitzing, Richard. "4D uniform polytopes (polychora) s3s4o3o - sadi".
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
Snub 24-Cell Derived from the Coxeter-Weyl Group W(D4) [1], Mehmet Koca, Nazife Ozdes Koca, Muataz Al-Barwani (2012);Int. J. Geom. Methods Mod. Phys. 09, 1250068 (2012)
Quaternionic representation of snub 24-cell and its dual polytope derived from E8 root system, Mehmet Koca, Mudhahir Al-Ajmi, Nazife Ozdes Koca (2011);Linear Algebra and its Applications,Volume 434, Issue 4 (2011),Pages 977-989,ISSN 0024-3795

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

Category:4-polytopes

DualSnub24Cell

The first failure of Gram's law occurs at the 127'th zero and the Gram point g₁₂₆, which are in the "wrong" order.

Caption1
Caption2

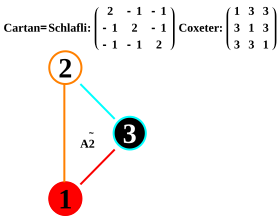
1 test 2 math>{\tilde{A}}_{2}</math> 3

4 5

${\tilde {A}}_{2}$ =[3^[3]]

Row	Lattice root system	Coxeter number	G₀	G₁	G₂	G_∞
1	Leech lattice (no roots)	0	1	2Co₁	1	Z²⁴
2	A₁²⁴	2	2²⁴	1	M₂₄	2¹²
3	A₂¹²	3	3!¹²	2	M₁₂	3⁶
4	A₃⁸	4	4!⁸	2	1344	4⁴
5	A₄⁶	5	5!⁶	2	120	5³
6	A₅⁴D₄	6	6!⁴(2³4!)	2	24	72
7	D₄⁶	6	(2³4!)⁶	3	720	4³
8	A₆⁴	7	7!⁴	2	12	7²
9	A₇²D₅²	8	8!²(2⁴5!)²	2	4	32
10	A₈³	9	9!³	2	6	27
11	A₉²D₆	10	10!²(2⁵6!)	2	2	20
12	D₆⁴	10	(2⁵6!)⁴	1	24	16
13	E₆⁴	12	(2⁷3⁴5)⁴	2	24	9
14	A₁₁D₇E₆	12	12!(2⁶7!)(2⁷3⁴5)	2	1	12
15	A₁₂²	13	13!²	2	2	13
16	D₈³	14	(2⁷8!)³	1	6	8
17	A₁₅D₉	16	16!(2⁸9!)	2	1	8
18	A₁₇E₇	18	18!(2¹⁰3⁴5.7)	2	1	6
19	D₁₀E₇²	18	(2⁹10!)(2¹⁰3⁴5.7)²	1	2	4
20	D₁₂²	22	(2¹¹12!)²	1	2	4
21	A₂₄	25	25!	2	1	5
22	D₁₆E₈	30	(2¹⁵16!)(2¹⁴3⁵5²7)	1	1	2
23	E₈³	30	(2¹⁴3⁵5²7)³	1	6	1
24	D₂₄	46	2²³24!	1	1	2

[FOOTNOTEHestenes2015-1] Hestenes 2015.

[FOOTNOTEDoranLasenby2003-2] Doran & Lasenby 2003.

[FOOTNOTELasenby2022-3] Lasenby 2022.

[FOOTNOTEKocaAl-AjmiKoca2011-4] Koca, Al-Ajmi & Koca 2011.

[1]

[2]

[3]

[4]