User:Cuddlyable3/Sandbox

and a fractal
[edit]A feature of the Mandelbrot set recently reported[1] gives a means to calculate an approximate value of to any chosen accuracy, without seeking the limit of an infinite series. One applies the iteration
where the complex number
where is the non-zero precision required, and counts the number of iterations until
i.e. stop when an iteration hits the circle radius 2 in the complex plane. The result is simply the approximation
In the graphical view one starts iterating from a point just above the bottom of the "seahorse valley" of the Mandelbrot set at (-0.75,0).

Multibrot sets
[edit]Multibrot sets[2] [3] are values in the complex plane that remain below some finite value throughout iterations by members of the general monic univariate polynomial family of recursions
The case of
is the classic Mandelbrot set from which the name is derived. The sets for other values of d also show fractal images[4] when they are plotted on the complex plane.
Each of the examples of various powers d shown below is plotted to the same scale. Values of c belonging to the set are black. Values of c that have unbounded value under recursion, and thus do not belong in the set, are plotted in different colours, that show as contours, depending on the number of recursions that caused a value to exceed a fixed magnitude in the Escape Time algorithm.
Positive powers
[edit]The example d = 2 is the original Mandelbrot set. The examples for d > 2 are often called Multibrot sets. These sets include the origin and have fractal perimeters, with (d-1)-fold rotational symmetry.
 |
 |
 |
 |
 |
Negative powers
[edit]When d is negative the set surrounds but does not include the origin. There is interesting complex behaviour in the contours between the set and the origin, in a star-shaped area with (d+1)-fold rotational symmetry. The sets appear to have a circular perimeter, however this is just an artifact of the fixed maximum radius allowed by the Escape Time algorithm, and is not a limit of the sets that actually extend in all directions to infinity.
 |
 |
 |
 |
 |
Rendering images
[edit]All the above images are rendered using an Escape Time algorithm that identifies points outside the set in a simple way. Much greater fractal detail is revealed by plotting the Lyapunov Exponent[5], as shown by the examples below. The Lyapunov Exponent is the error growth-rate of a given sequence. First calculate the iteration sequence with N iterations, then calculate the Exponent as 1/N * sum(ln(|f'(Z)|)) and if the Exponent is negative the sequence is stable. The white pixels in the picture are the parameters c for which the Exponent is positive aka unstable. The colours show the periods of the cycles which the orbits are attracted to. All points colored dark-blue (outside) are attracted by a fixed point, all points in the middle (lighter blue) are attracted by a period 2 cycle and so on.


Pseudocode
[edit]For each pixel on the screen do:
{
x = x0 = x co-ordinate of pixel
y = y0 = y co-ordinate of pixel
iteration = 0
max_iteration = 1000
while ( x*x + y*y <= (2*2) AND iteration < max_iteration )
{
/* INSERT CODE(S)FOR Z^d FROM TABLE BELOW */
iteration = iteration + 1
}
if ( iteration == max_iteration )
then
colour = black
else
colour = iteration
plot(x0,y0,colour)
}
The complex value z has coordinates (x,y) on the complex plane and is raised to various powers inside the iteration loop by codes shown in this table. Powers not shown in the table are obtained by concatenating the codes shown.
| z-1 | z2 (for Mandelbrot set) | z3 | z5 |
d=x^2+y^2 if d=0 then ESCAPE x = x/d y= -y/d |
xtmp=x^2-y^2 y=2*x*y x=xtmp |
xtmp=x^3-y*y*(x-2) y=y*(2*x+x*x-y*y) x=xtmp |
xtmp=x^5-10*x^3*y^2+5*x*y^4 y=5*x^4*y-10*x^2*y^3+y^5 x=xtmp |
An example of Python code for ASCII renderings of Mandelbrot, Multibrot, Julia and multi-Julia is at [6].
References
[edit]- ^ "π in the Mandelbrot set" (PDF).
- ^ "Definition of multibrots". Retrieved 2008-09-28.
- ^ "Multibrots". Retrieved 2008-09-28.
- ^ "Animated morph of multibrots d=-7 to 7". Retrieved 2008-09-28.
- ^ "An Investigation of Fractals Generated by z-->1/z^n + c, Ken Shirriff". Retrieved 2008-09-28.
- ^ "Python code". Retrieved 2008-09-28.
~





Uses as Counters
[edit]The repeating sequence of states of an LFSR allows it to be used as a divider, or as a counter when a non-binary sequence is acceptable as is often the case where computer index or framing locations need to be machine-readable. LFSR counters have simpler feedback logic than natural binary counters or Gray code counters, and therefore can operate at higher clock rates. However it is necessary to ensure that the LFSR never enters an all-zeros state, for example by presetting it at start-up to any other state in the sequence. The table of primitive polynomials shows how LFSR's can be arranged in Fibonacci or Galois form to give maximal periods. One can obtain any other period by adding to an LFSR that has a longer period some logic that shortens the sequence by skipping some state(s), e.g. as tabulated in [1].
Uses in Cryptography
[edit]An LFSR can generate an extremely long sequence which can be used to encrypt valuable information, for example by combining bits from the LFSR with information bits in an xor gate. The resulting bit stream can only be decrypted by a receiver equipped with the same LFSR, atarting at the same state. Although an attacker might know or discover the LFSR construction, as long as the starting state is kept as a secret key the attacker confronts a monstrous search problem.
Given an output sequence you can construct an LFSR of minimal size by using the Berlekamp-Massey algorithm.
Uses in Radio
[edit]- GPS satellite radionavigation
- CDMA cellular radio telephony
| Bits | Feedback polynomial | Period |
|---|---|---|
| n | ||
| 4 | 15 | |
| 5 | 31 | |
| 6 | 63 | |
| 7 | 127 | |
| 8 | 255 | |
| 9 | 511 | |
| 10 | 1023 | |
| 11 | 2047 | |
| 12 | 4095 | |
| 13 | 8191 | |
| 14 | 16383 | |
| 15 | 32767 | |
| 16 | 65535 | |
| 17 | 131071 | |
| 18 | 262143 | |
| 19 | 524287 | |
| 25 to 168 | [2] |
Approximations
[edit]Any digital generator of Gaussian pseudo-random samples must make these approximations.
- Truncate the tails that extend to infinite sample values. Two ways to do this are:
- see Fig. a). The result is part of a Gaussian distribution plus a uniform distribution with the same range
- see Fig. b). The result is a distorted (when normalised) part of a Gaussian distribution
- see Fig. c). Sample values must be quantised to fit the finite length of binary numbers in use.
- Truncate the tails that extend to infinite sample values. Two ways to do this are:
The sizes of these approximations must be chosen with regard to the intended use of the samples. Thus there is no single "right" choice.
Ziggurat algorithm
[edit]The motivation behind the ziggurat algorithm is that the majority of the samples of a non-uniform distribution such as the Gaussian that would be generated by calculating a transcendental (costly) can be provided instead by combining uniform distributions from PRNGs (cheap).
The PRNGs are assigned to layers of the area under the intended distribution curve. After above approximations, the layer areas on the left of the curve should be equal. They will be selected randomly by index and over long time each layer is selected the same number of times. (One may conveniently use a maximal-length n-bit PRNG shift register to select (2n-1) layers.)
A version of the algorithm described by Marsaglia, Tsang, Doornik et al. establishes a set of points on the curve using the approximation
xn(yn+1-yn) = A constant
These are equal-area rectangles that are larger, by varying degrees, than the curve-bounded areas that they include. The disproportionality means that corrresponding ranges of sample values are relatively under-represented in the output, whose distribution is distorted as shown in Fig. d). That distortion may be reduced (but not eliminated) by using more layers. The diagram shows the case of the coordinates provided here by anonymous user 71.41.210.146 .
Distortionless Ziggurat Algorithm
[edit]Two conditions together allow the distortion in Fig. c) to be avoided:
- Select layer coordinates that satisfy
erf(xn)-erf(xn+1)-yn(xn-xn+1)+xn+1(yn+1-yn)
- Whenever a sample is rejected at a layer, try again using a new PR sample to the same layer. Due to the rarity of such cases they do not slow the algorithm significantly.
[paste starts] This article would greatly benefit from illustrations. Also, are the injectors ever mounted directly over the cylinder head (replacing intake valves)? What is their injection pressure? What does an injector look like? Does it have a single or multiple outlet holes? I assume the output is an atomized mist, right?
As per your request I have drawn and uploaded a diagram to the front page of the article. An injector looks like a small syringe made of tough metal about 80mm long with a single outlet although theres a device in it so when it sprays the fuel comes out in tiny atomised globules rather than one continous stream of fluid. If there are any issues with the diagram please let me know here, I will be watching the page for approximately one month. ta --WikipedianProlific </wiki/User:WikipedianProlific>(Talk) </wiki/User_talk:WikipedianProlific> 18:23, 13 July 2006 (UTC) Please replace the label "GAS" with "FUEL". Objections to "GAS" have been thoroughly discussed in connection with the diagram of the Carburetor and they apply equally to the Fuel injector.Cuddlyable3 </w/index.php?title=User:Cuddlyable3&action=edit> 18:49, 8 February 2007 (UTC) I agree wholeheartedly. That has been bugging me for some time. The fual will not necessarily be petrol (gasoline). The intro of the autogas </wiki/Autogas> article also gives some background to why this is a problem. --Athol Mullen </wiki/User:AtholM> 21:58, 8 February 2007 (UTC) I have replaced the diagram with an animated one that receives FUEL, shows the solenoid winding and has removed unhelpful lines and legends.Cuddlyable3 </w/index.php?title=User:Cuddlyable3&action=edit> 15:56, 6 March 2007 (UTC) It's an excellent diagram you've put up, but I fear it will probably be deleted unless you re-upload it with proper copyright tagging. Just a note in the comment section saying you created it generally isn't sufficient to prevent such deletion, and it'd be a shame to lose this and the other images you've put together. It looks as if you've been alerted to this issue on your talk page, for pretty much every image you've uploaded. What is the difficulty you're experiencing selecting the applicable copyright tag from the dropdown menu on the upload screen...? --Scheinwerfermann </wiki/User:Scheinwerfermann> 19:14, 6 March 2007 (UTC) Thank you. I am not happy about some white spots that became evident to me after the animation was uploaded and resized. For each diagram I have loaded, I have checked "Public domain" but that has not prevented the automatic "untagged" warning that appears a little later. I am willing to try again. Cuddlyable3 </w/index.php?title=User:Cuddlyable3&action=edit> 21:11, 11 March 2007 (UTC) I have reverted the new animated diagram to the older static one. Please disregard the animated diagram until such a time as the mechanism it shows is more detailed and correct, if it is a point of contention then I shall do it myself. At the moment its[sic] an animated bastardisation of one of my diagrams: </wiki/Image:Fuelinjector.png> </wiki/Image:Fuelinjector.png>. There seems to be confussion[sic] about where compression occurs and the complex solenoid system is rather simplified. (WP:RPA) Even under the free license agreement I should still be credited on the images page for creating it, not just 'an improvement on another wikipedia diagram', the free license agreement allows one to edit my work shamelessly, but it doesn't permit one to take work without proper credit. I was unhappy with the quality of the two new diagrams, which I do not feel is up to wikipedia's standards. As a result I have redrawn them myself, Gas has been changed to Fuel by popular demand. WikipedianProlific </wiki/User:WikipedianProlific>(Talk) </wiki/User_talk:WikipedianProlific> 02:18, 18 March 2007 (UTC) Wikipedia warns anyone submitting work that it may be viewed critically and edited by anyone. I don't think a reversion becomes justified by the kind of language that WikipedianProlific is using here - words like "shamelessly" and "bastardisation" are ad hominem. Wikipedia provides traceability of contributions but is not the place to build a gallery of anyone's own art. I consider neither </wiki/Image:FuelInjector2.gif> </wiki/Image:FuelInjector2.gif>nor </wiki/Image:Fuelinjector.png> </wiki/Image:Fuelinjector.png>as beyond improvement and it may become necessary to ask for arbitration between them. I intend to wait a few days, and then possibly revert to whichever diagram gets more consensus. There is nothing to say here about "some rather unpleasent postings" that WP has since withdrawn from his user page.Cuddlyable3 </w/index.php?title=User:Cuddlyable3&action=edit> 15:59, 19 March 2007 (UTC) First off I mean no offense by use of words like bastardisation, it just means something thats the product of many different sources. Also I hope you don't mind but I resized those two images above just to save scrolling space and load times. I wish to point out that this isn't a revert war case. There was my original diagram. Then there was your animated version. Then there was my second diagram which was revised from the first diagram to resolve the issues that you had with it. The main reason I did this was because I had a few problems with your animation; 1.) There appears to be explusion of fuel from the nozzle prior to the spring moving forward, this isn't mechanically the case. 2.) I felt that the animation was not of a high enough level of quality compared with the static diagram to warrant is placement in the article. 3.) I was unhappy that although my work was submited under a free license agreement that it was not probably cited in your version. I am still entitled to be credited for its inception. However I realised at the time that you probably didn't know this and so let it slide, in future please be careful though. I wish to find a mutual resolution to this as I feel the need to point out that I really have no personal interest in it, I simply wish the article to be the best it can be, and I have no wish nor intention to upset you in that process. How would you feel about using both a corrected animated version and the static version? I Think they both add something to the article in there own way and that this may be a good solution? As for what has been said on my user page, (WP:RPA) I do not use wikipedia as an art gallery. I use deviantart.com and my own website as a gallery and none of these images are on either. What I do for wikipedia I do for free. The gallery on my userpage isn't a pompous exhibition of my 'skill', but rather a way for me to rapidly click on and access diagrams I've uploaded. It's like a list of quick links. It also serves as examples to people looking to request that I draw diagrams. Most of the work I do is by request, generally I don't seek out pages in need of art. WikipedianProlific </wiki/User:WikipedianProlific>(Talk) </wiki/User_talk:WikipedianProlific> 16:24, 19 March 2007 (UTC) [paste ends]
Regarding WikipedianProlific's comments:
There seems to be confussion[sic] about where compression occurs
- No compression of fuel occurs in the injector depicted. It is a valve not a pump.
the complex solenoid system is rather simplified.
- A solenoid-operated injector (not a piezo-operated injector) is depicted. The solenoid comprises
- A winding of insulated wire. The windings are shown in [2] consistently with the cut-away view but in [1] they are presumably meant to be understood by a draughtsman's shortcut of two crossed diagonal lines.
- A movable, spring-loaded ferromagnetic slug, shown blue in [2]
1.) There appears to be explusion of fuel from the nozzle prior to the spring moving forward, this isn't mechanically the case.
- The actual operating sequence is:
- i) No current in solenoid, spring relaxed, valve closed
- ii)Current in solenoid, spring compresses, valve opens
- iii)Fuel spray emitted
- iv) Return to i)
I agree that the 3-step animation looks ambiguous and that this is room for improvement.
Please disregard the animated diagram until such a time as the mechanism it shows is more detailed and correct, if it is a point of contention then I shall do it myself...How would you feel about using both a corrected animated version and the static version?
- You may copy freely anything of my work in Wikipedia that you find useful. When do you propose showing a new version?
Example .gif file
[edit]

The program Microsoft Paint v.6 in Vista saves a small black and white image as the following .gif file. Due to overhead code such as an unnecessarily large colour table this .gif file is not efficient for the image with only 15 pixels.
byte# hexadecimal text or
(hex) value Meaning
0: 47 49 46
38 39 61 GIF89a Header
Logical Screen Descriptor
6: 03 00 3 - width pixels
8: 05 00 5 - height pixels
A: F7 - GCT follows for 256 colors with resolution 3 x 8bits/primary
B: 00 0 - background color #0
C: 00 - default aspect ratio
R G B Global Color Table
D: 00 00 00 0 0 0 - color #0 black
10: 80 00 00 128 0 0 - #1
: :
85: 00 00 00 0 0 0 - color #10 black
: :
30A: FF FF FF 255 255 255 - color #255 white
30D: 21 F9 04 Graphic Control Extension
310: 01 - transparency is possible
311: 00 00 - delay for animation: not used
313: 10 16 - color #16 is transparent
314: 00 - end
315: 2C Image Descriptor
316: 00 00 00 00 (0,0) - scan pixels from left top...
31A: 03 00 05 00 (3,5) - ...to right bottom.
31E: 00 - end
31F: 08 8 LZW min. code size
320: 0B 11 11 bytes LZW encoded image data follow
321: 00 51 FC 1B 28 70 A0 C1 83 01 01
32C: 00 - end
32D: 3B GIF file terminator
Image coding
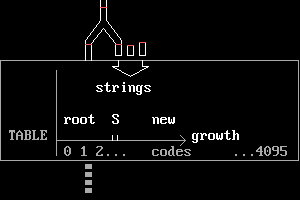
[edit]The image pixel colors, scanned horizontally from top left, are converted by LZW encoding to codes that are then mapped into bytes for storing in the file. For the sample image above the reversible mapping between 9-bit codes and bytes is shown below.
9-bit binary Bytes
(hex) (hex)
00000000 00
100
0101000|1 51
028
111111|00 FC
0FF
00011|011 1B
103
0010|1000 28
102
011|10000 70
103
10|100000 A0
106
1|1000001 C1
107
10000011 83
00000001 01
101
0000000|1 01
A slight compression is evident: pixel colors defined initially by 15 bytes are exactly represented by 12 code bytes including control codes. The encoding process that produces the 9-bit codes is shown below. A local string accumulates pixel color numbers from the palette, with no output action as long as the local string can be found in a code table. There is special treatment of the first two pixels that arrive before the table grows from its initial size by additions of strings. After each output code, the local string is initialised to the latest pixel color (that could not be included in the output code).
Table 9-bit
string --> code code Action
#0 | 000h Initialise root table of 9-bit codes
palette | :
colors | :
#255 | 0FFh
clr | 100h
end | 101h
| 100h Clear
Pixel Local |
color Palette string |
BLACK #40 28 | 028h 1st pixel always to output
WHITE #255 FF | String found in table
28 FF | 102h Add 1st string always to table
FF | Initialise local string
WHITE #255 FF FF | String not found in table
| 0FFh - output code for previous string
FF FF | 103h - add latest string to table
FF | - initialise local string
WHITE #255 FF FF | String found in table
BLACK #40 FF FF 28 | String not found in table
| 103h - output code for previous string
FF FF 28 | 104h - add latest string to table
28 | - initialise local string
WHITE #255 28 FF | String found in table
WHITE #255 28 FF FF | String not found in table
| 102h - output code for previous string
28 FF FF | 105h - add latest string to table
FF | - initialise local string
WHITE #255 FF FF | String found in table
WHITE #255 FF FF FF | String not found in table
| 103h - output code for previous string
FF FF FF | 106h - add latest string to table
FF | - initialise local string
WHITE #255 FF FF | String found in table
WHITE #255 FF FF FF | String found in table
WHITE #255 FF FF FF FF | String not found in table
| 106h - output code for previous string
FF FF FF FF| 107h - add latest string to table
FF | - initialise local string
WHITE #255 FF FF | String found in table
WHITE #255 FF FF FF | String found in table
WHITE #255 FF FF FF FF | String found in table
No more pixels
107h - output code for last string
101h End
Image decoding
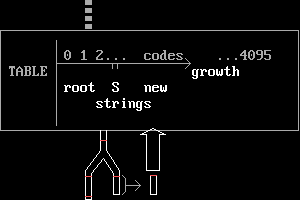
[edit]Decoding begins by mapping the stored bytes back to 9-bit codes. These are decoded to recover the pixel colors as shown below. A table identical to the one used in the encoder is built by adding strings by this rule:
Is incoming code found in table? YES: add string for local code followed by first byte of string for incoming code NO: add string for local code followed by copy of its own first byte
shift
9-bit ----> Local Table Pixel
code code code --> string Palette color Action
100h 000h | #0 Initialise root table of 9-bit codes
: | palette
: | colors
0FFh | #255
100h | clr
101h | end
028h | #40 BLACK Decode 1st pixel
0FFh 028h | Incoming code found in table
| #255 WHITE - output string from table
102h | 28 FF - add to table
103h 0FFh | Incoming code not found in table
103h | FF FF - add to table
| - output string from table
| #255 WHITE
| #255 WHITE
102h 103h | Incoming code found in table
| - output string from table
| #40 BLACK
| #255 WHITE
104h | FF FF 28 - add to table
103h 102h | Incoming code found in table
| - output string from table
| #255 WHITE
| #255 WHITE
105h | 28 FF FF - add to table
106h 103h | Incoming code not found in table
106h | FF FF FF - add to table
| - output string from table
| #255 WHITE
| #255 WHITE
| #255 WHITE
107h 106h | Incoming code not found in table
107h | FF FF FF FF - add to table
| - output string from table
| #255 WHITE
| #255 WHITE
| #255 WHITE
| #255 WHITE
101h | End
LZW code lengths
[edit]Shorter code lengths can be used for smaller palettes than the 256 (maximum) colors in the example. The code table initially contains codes that are one bit longer than the palette size in order to give additional space for two special codes clr and end and for strings that are added during the process. When the table is full the code length increases to give space for more strings, up to a maximum code 4095 = FFF(hex). As the decoder builds its table it tracks these increases in code length and it is able to unpack incoming bytes accordingly.
Animated .gif
[edit]An animated .gif file comprises a number of images or frames to be displayed successively, each described by its own GCE (Graphic Control Extension), preceded by a header whose content by default applies to all the frames. After the header the data is stream-oriented instead of being at fixed indices, so the location of the start of a GCE depends on the length of preceding GCE(s). Within a GCE the LZE-coded image data is arranged in blocks each of up to 255 bytes; the size of block is declared by a byte that precedes it. Below is the structure of the animated .gif at the start of this page:
byte# hexadecimal text or
(hex) value Meaning
0: 47 49 46
38 39 61 GIF89a Header
Logical Screen Descriptor
6: 90 01 400 - width pixels
8: 90 01 400 - height pixels
A: F7 - GCT follows for 256 colors with resolution 3 x 8bits/primary
B: 00 0 - background color #0
C: 00 - default aspect ratio
:
30D: 21 FF 0B Application Extension
310: 4E 45 54
53 43 41
50 45 32
2E 30 NETSCAPE2.0
31B: 03 01 FF
FF 00
320: C1 F9 04 Graphic Control Extension frame #1
323: 08 - no transparency
324: 09 00 - 0.09 sec delay
325: 00 - no transparent color
327: 00 - end
328: 2C Image Descriptor
329: 00 00 00 00 (0,0) - scan pixels from left top...
32D: 90 01 90 01 (400,400) - ...to right bottom
331: 00 - end
332: 08 8 LZW min code size
333: FF 255 255 bytes LZW encoded image data follow
334: data
433: FF 255 255 bytes LZW encoded image data follow
data
:
92BA: 00 end
92BB: C1 F9 04 Graphic Control Extension frame #2
: :
153B7B:C1 F9 04 Graphic Control Extension frame #44
:
15CF35:3B 1 429 301 File terminates
The GCEs allow the time for which each frame is displayed to be specified in hundredths of second. Some economy os data is possible where a frame need only rewrite a portion of the pixels of the display, because the Image Descriptor can define a smaller rectangle to be rescanned instead of the whole image. Displays that do not support animated .gifs show only the first frame.
An Admin is needed to block Greg_L
[edit]I cuddlyable3 am a relative newbie and now contribute mainly to mathematical articles. I am experiencing such mounting disruptions to editing from Greg_L that action is needed by an admin to enforce WP:POINT based on defiant incivility and admitted untruths by Greg_L. This archived WQA raised by Thunderbird2 is Closed as Stuck. That is because block sanctions that were discussed cannot be issued from WQA. I do not see that any of the editors who contributed in the WQA (excluding the two users implicated) condoned the behaviour of Greg_L. My involvement has been can be seen in the strikeouts of falsehoods that Greg_L introduced. This summary is my opinion of what needs to be done (by an admin).
Short history
[edit]I have had contact with Greg_L only since 4/5/6 November 2008 when his entries at [3] brought in a level of combativeness unsuited to the civil way that editors on a mathematics related article normally collaborate.
I see that Greg_L is regularly cited in complaints including those arising in this 2-year debate, by Wolfkeeper and this by Omegatron last June.
Actions already tried:
[edit]A WQA from me, Reaction by Greg_L.
A 12-hour block by Ryan Postlethwaite
My message wishing for civil collaboration to which Greg_L replied acceptably on his Talk page but then quoted the message with derision ("Imagine my surprise, when I see this ‘let’s let bygones be bygones & work together in peace’-post from you..") in the WQA.
My offer to go to mediation has been deleted by Greg_L without comment.
I have notified Greg_L of this request to WP:ANI. Cuddlyable3 (talk) 22:07, 18 February 2009 (UTC)
ASCII graphics
[edit]FONT
!"#$%&'()*+,-./ 047
0123456789:;<=>? 063
@ABCDEFGHIJKLMNO 079
PQRSTUVWXYZ[\]^_ 095
`abcdefghijklmno 111
pqrstuvwxyz{|}~⌂ 127
ÇüéâäàåçêëèïîìÄÅ 143
ÉæÆôöòûùÿÖÜø£Ø׃ 159
áíóúñѪº¿®¬½¼¡«» 175
░▒▓│┤ÁÂÀ©╣║╗╝¢¥┐ 191
└┴┬├─┼ãÃ╚╔╩╦╠═╬¤ 207
ðÐÊËÈıÍÎÏ┘┌█▄¦Ì▀ 223
ÓßÔÒõÕµþÞÚÛÙýݯ´ 239
±‗¾¶§÷¸°¨·¹³²■ 255
FONT
!"#$%&'()*+,-./ 047
0123456789:;<=>? 063
@ABCDEFGHIJKLMNO 079
PQRSTUVWXYZ[\]^_ 095
`abcdefghijklmno 111
pqrstuvwxyz{|}~⌂ 127
ÇüéâäàåçêëèïîìÄÅ 143
ÉæÆôöòûùÿÖÜø£Ø׃ 159
áíóúñѪº¿®¬½¼¡«» 175
░▒▓│┤ÁÂÀ©╣║╗╝¢¥┐ 191
└┴┬├─┼ãÃ╚╔╩╦╠═╬¤ 207
ðÐÊËÈıÍÎÏ┘┌█▄¦Ì▀ 223
ÓßÔÒõÕµþÞÚÛÙýݯ´ 239
±‗¾¶§÷¸°¨·¹³²■ 255
ABCDEIF
!"#$%&'()*+,-./ 47
0123456789:;<=>? 63
@ABCDEFGHIJKLMNO 79
PQRSTUVWXYZ[\]^_ 95
`abcdefghijklmno 111
pqrstuvwxyz{|}~? 127
€‚ƒ„…†‡ˆ‰Š‹ŒŽ 143
‘’“”•–—˜™š›œžŸ 159
¡¢£¤¥¦§¨©ª«¬®¯ 175
°±²³´µ¶·¸¹º»¼½¾¿ 191
ÀÁÂÃÄÅÆÇÈÉÊËÌÍÎÏ 207
ÐÑÒÓÔÕÖ×ØÙÚÛÜÝÞß 223
àáâãäåæçèéêëìíîï 239
ðñòóôõö÷øùúûüýþÿ 255
.!"#$%&'()*+,-./ 47
0123456789:;<=>? 63
@ABCDEFGHIJKLMNO 79
PQRSTUVWXYZ[\]^_ 95
`abcdefghijklmno 111
pqrstuvwxyz{|}~? 127
€‚ƒ„…†‡ˆ‰Š‹ŒŽ 143
‘’“”•–—˜™š›œžŸ 159
¡¢£¤¥¦§¨©ª«¬®¯ 175
°±²³´µ¶·¸¹º»¼½¾¿ 191
ÀÁÂÃÄÅÆÇÈÉÊËÌÍÎÏ 207
ÐÑÒÓÔÕÖ×ØÙÚÛÜÝÞß 223
àáâãäåæçèéêëìíîï 239
ðñòóôõö÷øùúûüýþÿ 255
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▀▄
▄▄▀▀▀▀▀▀▀▄▄ ▀▄
▄▀ ▀▄ ▀▄
▄▀ ▀▄ ▀▄
▄▀ ▀▄ ▀▄
█ █ ▀▄
█ █ ▀▄
█ █ ▀▄
█ █ ▀▄
▀▄ ▄▀ ▀▄
▀▄▄ ▄▄▀ ▀▄
▀▀▀▀▀▀▀ ▀▄
▀▄
▀▄
▀▄
▀▄




























