User:AmritAndAsh

Origami Numbers

When we consider origami in a mathematical sense, it is the idea of being able to construct a line of any length we like by using a finite number of folds on a piece of paper. Cutting the paper is traditionally not allowed in the construction of these numbers, instead you rely on creating reference points by making intersections using folds and creases. This leads to the formal definition;

A real number r is origami-constructible if one can construct in a finite number of steps two points which are a distance of |r| apart.

History

Origami is the art of folding paper, originating in Japan. You begin with a square piece of unmarked paper and using reference points created through creases and folds you are able to construct different shapes as well as lines of differing lengths. These constructed lines and shapes were traditionally made using Greek methods of an unmarked ruler and compass.

The word origami comes from the Japanese words oru (to fold) and kami (paper).

Despite the long history of using a compass and straight edge to construct numbers; commonly referred to as Euclidean Constructions due to their relationship to Euclid's Elements dating back to ancient Greece; the method of origami has only taken off in the past century - starting with the Huzita Axioms.

While a 'constructible' number is a real number, r, given a line segment of unit length, a line segment of length |r| can be constructed with a compass and straightedge (a ruler with no markings) in a finite number of steps. However, there was restriction in this method, there were three constructions that could not be done via Euclidean Construction: Squaring the Circle (Constructing a square with area pi); Doubling the Cube (Constructing a line segment of length ${\sqrt[{3}]{2}}$ ); and Trisecting an Angle - whereas these can be done easily by the use of origami.

Huzita Axioms

The Huzita–Hatori or the Huzita–Justin axioms, are a set of principles that are used to describe the operations that can be made when folding a piece of paper. The operations are assumed to be used on a plane with linear folds. There are seven axioms in total. The first six were initally discovered in 1986, before being published by Humiaki Huzita in 1991. Then the seventh axiom was discovered in in 1989 by Jacques Justin, and then rediscovered in 2001 by Koshiro Hatori.

Details of each axiom

Axiom 1

Given two points p₁ and p₂, there is a unique fold that passes through both of them, connecting them.

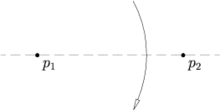
Axiom 1

Axiom 2

Given two points p₁ and p₂, there is a unique fold in order to fold p₁ onto p₂

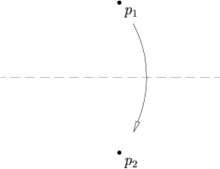
Axiom 2

Axiom 3

Given two lines l₁ and l₂, there is a fold in order to fold line l₁ onto l₂

Axiom 3

Axiom 4

Given a point p₁ and line l_1, there is a unique fold perpendicular to l₁, passing through the point p₁

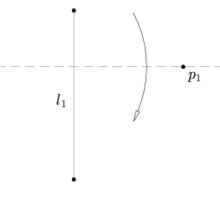
Axiom 4

Axiom 5

Given two points p₁ and p₂ and line l_1, there is a unique fold in order to fold p₁ onto l₁ and passes through the point p₂

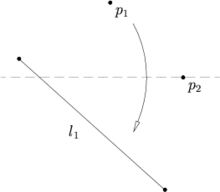
Axiom 5

Axiom 6

Given two points p₁ and p₂ and two lines l₁and l_2, there is a fold that places p₁ onto l_1,and places p₂ onto l₂

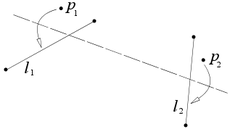
Axiom 6

Axiom 7

Given one point p and two lines l₁ and l₂, there is a fold that places p onto line l₁ and is perpendicular to l₂

Axiom 7

Constructions

Using the Huzita-Hatori axioms, it is possible to solve some of the Greek problems that could not be solved. This section will cover how to use Origami to solve Trisecting an Angle and Doubling the Cube.

Trisecting an Angle

Using Origami constructions, it is possible to trisect an angle. This was not possible when using Euclidean Constructions.

Trisecting an Angle

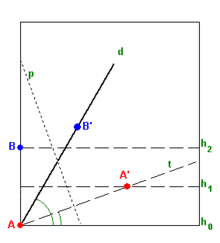
This can be done using any angle, but the following method is for angles below 90°. For this walk-through, we're going to be trisecting 90° itself. Following the diagram above;

1. First, make a horizontal fold anywhere across the square, creating line Bh₂. (This is a mixture of Axiom 2, 3 and 4).
2. Now fold line Ah₀ up to meet line Bh₂, creating line h₁. (Axiom 3)
3. Next, fold the corner of A up so that it touches line h₁ and so that B stays where it is, creating point A'. This also creates line p. (Axiom 2).
4. With the corner still folded, follow the crease created by line h₁, folding along it to create line d.
5. Unfold the corner and extend line d down to point A.
6. Finally, fold line Ah₀ up until it is on top of line d, creating fold line t. (Axiom 2).
7. The angle has then been trisected.

It is important to note that if you wish to trisect an angle that is less than 90°, choose a point C along the top of your square paper in order to create that angle between that point, A and h₀. Then, in Step 3, fold it so that point B touches the line AC and A touches h₁. This creates the two points A' and B' respectively.

Doubling the Cube

The idea of "Doubling the Cube" means that suppose you have a cube with side length S₁ and volume V; you are to find the side length S₂ that makes the cube with volume 2V.

Doubling the Cube

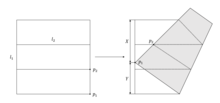
Following the image above;

1. First, make a small fold half-way up the right hand edge of the paper. We will name this point p₃. (Again, a mixture of Axiom 2, 3 and 4).
2. Next, apply Axiom 1 to connect the top left corner and the bottom right corner with a line. Do the same with the bottom left corner and point p₃.
3. Fold the top edge down to meet the intersection of these two lines. This creates line l₂. (Axiom 2 or Axiom 3)
4. Unfold that, and then fold the bottom edge up to meet with the new crease that you just created. The right edge point of this new crease we will name p₂. (Axiom 3)
5. Fold point p₁ up until both p₁ lies on l₁ and p₂ lies on l₂. (Axiom 6)
6. Point p₁ then divides up line l₁. Work out the ratio X/Y where X is the length of the top corner down to p₁ and Y is the length of p₁ down to the bottom right corner. Multiply S₁ by this ratio and this gives you the length of S₂.

Origami-Constructible Numbers as a Subfield

The origami-constructible numbers form a subfield of $\mathbb {C}$. That is to say that the field of origami-constructible numbers is contained within $\mathbb {C}$ and satisfies the field axioms with the same operations as $\mathbb {C}$.

This can be proved by applying the Huzita Axioms!

Before we can do this however, we first need to define two more Axioms that are made by composing the Huzita Axioms; which will help prove the operations. These will be referred to as the Elementary Operations;

E1. Given a point p and a line l, fold a line parallel to l that goes through p

This is constructed using two applications of Axiom 4, i.e. the first application provides line l₁ , which is a line perpendicular to our original l. Applying the Axiom once more to l₁ creates line l₂ which is perpendicular to l₁ , meaning it is also parallel to l.

E2. Given a point p and a line l, reflect p across l.

This is constructed by applying Axiom 4 and then Axiom 5 to the result.

Now that we have these two Axioms and the Huzita Axioms, we can prove that the field of origami-constructible numbers form a subfield of $\mathbb {C}$.
We do this by checking Addition, Multiplication and Inversion. This is to say, given origami-constructible numbers $\alpha$ and $\beta$, $\alpha$≠0 in $\mathbb {C}$, $\alpha$+$\beta$, $\alpha$$\beta$ and $\alpha ^{-1}$ are also in $\mathbb {C}$.

Addition

Regular Parallelograms

The proof starts out with three points: 0, p₁ and p₂. Using Axiom 1 it is easy to create the lines l₁ and l₂.

From here, use E1 to construct l₃. That is, use E1 in regards to p₁ and l₂.

Similarly, use E1 to construct l₄. This construction involves p₂ and l₁.

It is clear then that p₃ is the point of intersection of the two constructed lines l₃ and l₄.

Visual aid to describe addition of origami numbers in complex field (made by us)

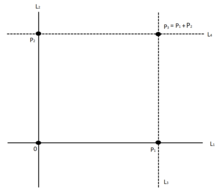
Degenerate Parallelograms

If the points p₁ and p₂ are scalar multiples of each other (i.e. lie on the same line from 0) this method cannot be used.

As before, begin by using Axiom 1 to create the starting line l₁, this time going through 0, p₁ and p₂. Then, apply Axiom 2 to fold p₂ onto p₁ and leave the paper folded over. Thus, p₃ is now on top of 0 (in the same spot). To create the intersection crease, apply Axiom 4 to 0 and the original line l₁. This creates the intersection marking p₃.

Multiplication

One important thing to note about Multiplication is that because origami-constructed numbers are being shown to be a subfield of the Complex field, they can either be multiplied by a Real number or $\imath$.

Real Number Multiplication

To start, we are going to assume that p₁ is not a real number. If it is, add $\imath$ to it and then apply Axiom 4 to project it onto the Real axis.

We begin with four points; 0, 1, r, and p₁. It is obvious that r is a scalar multiple of 1 (multiplied by r) so they begin along the same line from 0. When multiplying a number p₁ by a real number r we use the following steps;

First; apply Axiom 1 to 0 and p₁ to create our first line l₁ through both those points.

Similarly, apply Axiom 1 to p₁ and 1 to create our second line l₂ through both of these points.

From here, apply E1 to r and l₂ to create l₃, the line that goes through r, parallel to l₂.

Here it is obvious that p₃ is created using the intersections of lines l₁ and l₃.

Multiplication by $\imath$

Multiplying a number by $\imath$ means to rotate it counter-clockwise around the point 0, $\pi /2$ radians. To do this, we simply need to follow these steps;

Start with 2 points 0 and p₁. Apply Axiom 1 to create the first line l₁ through these two points.

Next, apply Axiom 4 on the point 0 and the line l₁ to create l₂, the line perpendicular to l₁ through the point 0.

Now apply Axiom 3 on the lines l₁ and l₂ to create line l₃, the line that bisects the angle between them.

Finally apply E2 to point p₁ and line l₃ to create point p₂.

Inversion

To find the inverse of a complex number in terms of origami-constructible numbers, we simply divide by a real number, making the process almost identical to multiplying.

Start with four points 0, 1, r and p₁. First, create line l₁ by applying Axiom 1 to 0 and p₁, creating the line through them.

Similarly, apply Axiom 1 to r and p₁ to create line l₂, the line through those two points as well.

Next, apply E1 to the point 1 and line l₂ to create line l₃, the line parallel to l₂ through the point 1.

Now the intersection of l₁ and l₃ is clear, which we mark as point p₃.

Future of Origami and Further Uses

People have found the mathematics of origami to have many practical uses in various fields, such as space travel and observation; robotics and medicine. For example, engineers have designed a 'star shade' to help observe exoplanets for use in space telescopes. There have also been origami usage in medicine. For example, compact devices such as oriceps for use in robotic surgery.

Some are changing the way we look at origami in mathematics. By fusing origami with the Ancient Greek method of using a compass, three more axioms were discovered in 2011 by researchers at University of Tsukuba. These new axioms allowed the construction of more structures such as ellipses and hyperbolas. They also allow another method of trisecting an arbitrary angle.

Some are trying to explore further extensions in origami, for example, allowing use of cutting and tracing. Typically, in origami these things are not permitted, however they can have significant mathematical impact. For example, if cutting is used as well as paper-folding, then we would possibly be able to superimpose points and lines by cutting the paper into two seperable parts and placing one on top of the other. This idea can also be seen if we allow the use of tracing. These ideas can allow many more constructions to be possible. Another idea that can be explored is using non-flat surfaces for the origami, such as spheres and paraboloids.