Talk:Wavelength/Archive 1
| This is an archive of past discussions about Wavelength. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. |
| Archive 1 | Archive 2 | Archive 3 | → | Archive 5 |
Question
how do you find wavelength? —Preceding unsigned comment added by 152.163.101.10 (talk) 01:26, 17 April 2005 (UTC)
Redirect change
I suggest that de Broglie wavelength redirects to de Broglie hypothesis, not here. It makes more sense, and de Broglie hypothesis has a much better description. Perhaps a rewrite is then needed of that section of this page to reflect that. Any objections?
--Blinken 11:45, 27 Apr 2005 (UTC)
- I can't believe it redirects here instead of de Broglie hypothesis already. I went ahead and changed it, figuring I should be bold. In light of that, the section in here about the de Broglie wavelength probably does need to be rewritten and shortened a bit. --Laura Scudder | Talk 19:36, 27 Apr 2005 (UTC)
- Went ahead and moved it over. --Blinken 02:19, 4 May 2005 (UTC)
Lambda = C / f
Would it be worth using the more general formula here, instead of ? Or perhaps mentioning that the formula can be used with other waves by replacing the speed of light with the speed of the individual wave? --Defragged 13:23, 13 Jun 2005 (UTC)
- Yes -- Tim Starling 04:11, Jun 14, 2005 (UTC)
relationship between Wavelength and the distance covered by the waves
Hey All !
is there any difference between the Wavelength and the distance covered by a MICOR WAVE when radiated through an anteena. Bascially i am confuse, what difference a wavelength make in the tranmisstion of a wave ? like do Higher Wavelength waves need less power to radiate and vice vers. Also what is the maximum range a micro-wave can travel or it can travell to unlimited distance (increasing the radiation in the area as a drawback ?) . I would be grateful if someone clear this up.
regards, Shakeel Ahmad —Preceding unsigned comment added by 66.198.93.7 (talk) 13:50, 4 July 2005 (UTC)
- In a vacuum, electromagnetic radiation of any wavelength can travel for an unlimited distance, with intensity decreasing with distance due to the larger area as you suggest. When travelling through a medium, some will be absorbed, and the amount absorbed depends on the wavelength. That's not the major practical distance when talking about communications though, which I'm guessing you are. The major difference is that smaller wavelengths (higher frequencies) can carry more information than longer wavelengths. The downside is that higher frequencies need more expensive circuitry to send and receive. In general, smaller wavelengths are more strongly absorbed than longer wavelengths, although this is only a minor nuisance for most communications applications. -- Tim Starling 03:26, 8 December 2005 (UTC)
measurement?
how does one measure wavelength?? --129.11.76.216 12:01, 26 April 2006 (UTC)
- simply by noting the peaks in activity upon the measuring body.
- Incidentally, the sine curve model and the use of the term 'wavelength' are a bit misleading when used to describe the physical movement of a photon. It doesn't literally move in a path following the sine wave curve, it moves in a straight line, it's just that its intensity varies as a sine wave along said straight line. Peak follows peak through the medium. In pure vacuo all photons travel at c, the speed of light, photons of higher energy are merely able to create more concentrated peaks on their journey. Electromagnetic radiation is really a product of space-time behaviour, rather than something 'passing through' space-time, as it were. Martyn Smith 22:33, 14 July 2006 (UTC)
- What is the unit of measurement for wavelength?
- please cite your sources.§ Marcher Lord
- Nevermind that, it's just units of measurement of length, I looked on
- § Marcher Lord
Describing Wave Image
"The x axis represents distance, and I would be some varying quantity at a given point in time as a function ..."
Be nice to see some labels on the image. Also the italicised "I" looks like a forward slash, and is not immediately obvious as to how it relates to the tipped-over "I" from the image.
--Thangalin 26 Sep 2006 (PST)
Wavelength, frequency, type of wave, and energy in joules
Does anyone know the equations to figuring out all of these with just one? PatPeter (talk · contribs) 20:50, 5 January 2007 (UTC)
Where symbol lambda come from?
Hi, does anyone know where the symbol of wavelegth is derived? Perhaps from greek word, but what is that word? Sorry my bad english --213.186.244.119 11:29, 18 August 2007 (UTC)
- My guess would be from the word length (longueur, lengte, längd, länge, lunghezza in various languages). That's how you usually pick a symbol: if the Latin letter isn't available, you take a similar-sounding Greek letter. It would be nice to have a reference and add it to the article, though. Han-Kwang (T) 12:21, 18 August 2007 (UTC)
- Lambda is the 11th letter of the greek alphabet... wikipedia has an article all about it
- http://en.wikipedia.org/wiki/Lambda
- —Preceding unsigned comment added by Curtis.Everingham (talk • contribs) 04:43, 18 October 2007 (UTC)
The Speed of Light
"The speed of light in most media is lower than in vacuum ..."
Could someone name me a medium where light travels faster than it does in a vacuum? 80.42.146.135 17:23, 25 October 2007 (UTC)
- No such medium exists in are universe. The speed of light is relative to the universe you live in, for us it's 299,792,458 meters per second max... This absolute limit makes space travel a real bitch because 299,792,458 m/s is very slow when compared to the size of the observable universe, which is 863,990,470,000,000,000,000,000,000 meters in diameter. It would take 91,325,815,300 years to travel from one end to the other in a space ship moving at the speed of light. Getting the space ship up to the speed of light would require all the energy in the universe. :-( —Preceding unsigned comment added by 98.214.11.170 (talk • contribs) 18:12, 2 April 2008 (UTC)
- Assuming the calculations above are correct, how can it take 91 billion years to travel from one end of the universe to the other at the speed of light, given that the age of the universe is estimated to be only 14 billion years old? Matter would have to be traveling at over 63,064,997,800,000,000 m/s to make 14 billion years work. I'm confused?—Preceding unsigned comment added by 216.73.235.7 (talk • contribs) 20:54, 2 April 2008
- because (i think) the expansion of the universe is not just the movement of matter, but also a stretching of space itself, which allows the universe to expand much faster than would be limited by your logic, especially during the early stages of the universe's expansion, however im not an expert, and this is just something i recall seeing somewhere, i cant cite it —Preceding unsigned comment added by 193.60.83.241 (talk • contribs) 13:55, 16 May 2008
Wavelength Error?
The audible hearing frequency is listed on the page as being between 17 m and 17 mm. I believe the correct numbers are 17 km and 17 Mm. 138.32.32.166 16:57, 1 November 2007 (UTC)
- The speed of sound is not the speed of light. Han-Kwang (t) 19:53, 1 November 2007 (UTC)
- That's not the same kind of wave though. Maybe this article should only concern itself with electromagnetic waves that are governed by the speed of light, or split them into separate sections. The problem is that the speed of sound is not a universal constant. If I were in a submarine, an air plane, in space, or on another planet those numbers wound be way off. —Preceding unsigned comment added by 98.214.11.170 (talk) 17:04, 2 April 2008 (UTC)
- Wavelength is wavelength, for light waves, sound waves, water waves, etc., irrespective of the propagation speed of the wave. And phase speed is wavelength times frequency. Those are general physics principles and relationships. I do not think it useful to split this article in sections for the many existing kinds of wave phenomena. If the examples, given to clarify the concepts, lead to confusion, they have to be improved. Crowsnest (talk) 17:53, 2 April 2008 (UTC)
- Actually the wavelength of light changes in any medium from its free-space value. We define the frequency as staying the same, so it is incorrect to list the range of human hearing in a wavelength format. The frequency remains the same regardless of the medium it travels in; this is why human hearing is almost always written in Hz. —Preceding unsigned comment added by 128.61.50.94 (talk • contribs) 22:05, 23 November 2008 (UTC)
- Wavelength is wavelength, for light waves, sound waves, water waves, etc., irrespective of the propagation speed of the wave. And phase speed is wavelength times frequency. Those are general physics principles and relationships. I do not think it useful to split this article in sections for the many existing kinds of wave phenomena. If the examples, given to clarify the concepts, lead to confusion, they have to be improved. Crowsnest (talk) 17:53, 2 April 2008 (UTC)
- That's not the same kind of wave though. Maybe this article should only concern itself with electromagnetic waves that are governed by the speed of light, or split them into separate sections. The problem is that the speed of sound is not a universal constant. If I were in a submarine, an air plane, in space, or on another planet those numbers wound be way off. —Preceding unsigned comment added by 98.214.11.170 (talk) 17:04, 2 April 2008 (UTC)
School Project?
I gotta write some thing for science about wave length and my teacher said nit has to be a wikipedia page. Can someone make a page for me? —Preceding unsigned comment added by Foz77 (talk • contribs) 18:52, 21 January 2008 (UTC)
Only propagating waves
The article focuses entirely on propagating waves, while wavelength is a property of spatial wave patterns which do not have to propagate or move at all. How about generalizing this article to spatial wave patterns, not necessarily propagating? Crowsnest (talk) 11:39, 10 April 2008 (UTC)
Visible spectrum by wavelength in web colors
The link I added to http://www.magnetkern.de/spektrum.html (the visible electromagnetic spectrum displayed in web colors with according wavelengths) was reverted by another user with the reason that a german site is not suitable. The page is bilingual (english and german) and contains references to english sources, so I cannot understand the reasons for deleting the link. There is also a discussion about the wavelength table on the discussion page of the Color article. Jan 85.179.9.12 (talk) 10:40, 26 June 2008 (UTC)
- I re-instated the link. Crowsnest (talk) 11:17, 26 June 2008 (UTC)
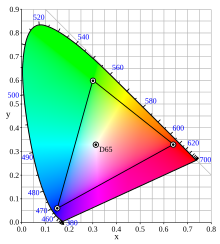
- Indeed I overlooked the fact that there was English text on the page as well. But in any case, I find it somewhat dubious to claim that this is "the" way to map wavelengths to sRGB, for two reasons. The first is that the vast majority of consumer-grade LCD monitors doesn't even come close to sRGB, both in terms of the gamma and the positions of the R/G/B primaries. The second is that it is an arbitrary choice to simulate wavelengths larger than 611 nm by mixing in blue, i.e. simulating redder than red by making it purple. On the blue side it makes some sense since the red cones have some absorption in the blue, but it doesn't work the other way around. I understand that the idea behind it was that the straight line from the white point to the 700 nm crosses the boundary of the sRGB gamut somewhere along the purple line, but I fail to see why this is a "better" method than simply clipping at the edge of the gamut, with #ff0000 representing all wavelengths longer than 611 nm.
- The picture below is IMO the best one can do to simulate the color spectrum on sRGB. I was actually somewhat involved in the design of it (see Talk:Color_blindness/Archive1).

Han-Kwang (t) 12:08, 26 June 2008 (UTC)
- I agree that your picture is very nice. For getting a good impression of the visible spectrum, it's neccessary to fade out the lightness on the borders of the spectrum. The table behind the link is not doing that, but aiming more to be a translation table for a particular wavelength (e.g. to be used in articles), being as accurate as possible. So the two approaches are aiming for two different problems. I still think my translation table is quite handy, and I did not find any other table like that on the web (yet). Perhaps, if this discussion comes to the conclusion that red with long wavelengths needs to have a more purple sRGB-hue than the sRGB primary red, you might want to change your picture according to it (if it doesn't make too much work). Anyway your picture already gives a better overview about the visible spectrum than the table. Jan 85.179.23.127 (talk) 10:12, 28 June 2008 (UTC)
- The trick in this picture is that the background is grey, rather than black. That way, you can make negative RGB values to cover colors outside the sRGB gamut. A possible criticism is that I'm not sure whether we used sRGB or NTSC primaries, and that a gamma of 2.5 was assumed rather than 2.2 (or the weird gamma-like function that is used in sRGB). Han-Kwang (t) 18:00, 29 June 2008 (UTC)
- Yes, I already suspected that the grey was used to expand the gamut; it is a nice way of solving the problem. Can you explain me why your program did not chose purple colors for "deep red", as my program and the images of the Green Flash page did? I don't think anymore that its as much neccessary to make a mixture with blue, but I would like to know if you explicitly prohibited blue colors appearing, or if the mechanism just got that results "naturally". The weird gamma-like function is corresponds almost to gamma 2.2, but contains a linear part to avoid numerical computation errors ("The effect of the above equations is to closely fit a straightforward gamma 2.2 curve with an slight offset to allow for invertability in integer math." [1]). Jan 85.179.15.103 (talk) 22:28, 29 June 2008 (UTC)
- Even if you can compensate the need to mix in additional blue with the grey background, that would mean you'd have to reduce green (i.e. "negative green"), if I overlook it correctly. But at 660nm I get #b8443d with a color picker (so more red and green than anything else, and more green than the background #414141). You can calculate linear (non-gamma corrected) sRGB values for 660nm light using the CIE standard colorimetric observer data for 2° (X, Y, Z) at 660nm, and the transfomration matrix of the sRGB standard to convert from XYZ values to linear RGB:
660nm: X=0.164900; Y=0.061000; Z=0.000000 R[sRGB] = 3.2410 * X - 1.5374 * Y - 0.4986 * Z = 0.4406595 G[sRGB] = - 0.9692 * X + 1.8760 * Y + 0.0416 * Z = -0.04538508 B[sRGB] = 0.0556 * X - 0.2040 * Y + 1.0570 * Z = -0.00327556
- You can see that the smallest value of the three RGB primaries is for green (actually negative), which is not the case in your image. Of course this might be changed when considering the Abney effect and/or other color appearance effects as adding grey can shift the perceived hue, but did your program creating the image as shown here consider this and/or other appearance effects? Jan 85.179.4.11 (talk) 09:50, 1 July 2008 (UTC)
- I do not read anywhere that they claim this to be "the" way to map wavelengths to sRGB. In general, such a kind of mapping seems handy, so this link or another one seems appropriate in the article: there is a somewhat similar link for wavelength-frequency conversion. A point of concern is the reliability and verifiability of this source: do you know a more reliable one which is verifiable? -- Crowsnest (talk) 15:55, 26 June 2008 (UTC)
- I had a brief look at the source code, but it is written in a fairly obscure language (i.e., not comprehensible by me) and the code is quite long, and it is not stated in simpler terms what it does (I assume it preserves the hue angle from a D65 white point, but the choice of white point is quite arbitrary). I do not know a more reliable/verifiable one, but as I explained above, I don't think a reliable mapping exists. Moreover, I don't think this type of external link belongs in the wavelength article anyway - next we'll get a DeBroglie calculator, water wave calculator, earthquake wave calculcator, gravity wave calculator and so on. Apart from that I'd like to mention that 85.179.9.12 (talk · contribs) and 85.179.18.203 (talk · contribs) are from the same German ISP and their whole contribution list consists of adding/discussing these links. The external links policy prohibits adding links to sites one is affiliated with, which seems quite likely here - they added the same link twice on different articles. Han-Kwang (t) 16:48, 26 June 2008 (UTC)
- Sorry, I was not aware of that policy. Remove the link, if you don't find it useful, or just copy the data to wikipedia according to the granted rights: "You may freely copy, modify, merge or use this data collection. I do not assure that the data is correct. Use at your own risk." The whitepoint is D65 according to the sRGB standard. That "obscure" language is Haskell (also mentioned in the first sentence of the introductory comment in the source), a very modern functional programming language. Jan 85.179.0.13 (talk) 19:29, 27 June 2008 (UTC)
- The fact that Haskell is very modern does not mean that it is not obscure. Obscure means unknown or difficult to understand, which I dare say is the case for the vast majority of people who do some kind of programming, including me.[2] :-) Han-Kwang (t) 23:17, 27 June 2008 (UTC)
- Sorry, I was not aware of that policy. Remove the link, if you don't find it useful, or just copy the data to wikipedia according to the granted rights: "You may freely copy, modify, merge or use this data collection. I do not assure that the data is correct. Use at your own risk." The whitepoint is D65 according to the sRGB standard. That "obscure" language is Haskell (also mentioned in the first sentence of the introductory comment in the source), a very modern functional programming language. Jan 85.179.0.13 (talk) 19:29, 27 June 2008 (UTC)
- Functional programming is really tricky, if you have mostly imperative or object-oriented experiences. And as most people are using imperative or object-oriented languages, I agree that a program written in that language is not easy to comprehend for many people. But I think in university or computer science context Haskell is quite common, and I think it's one of the "standard" languages for functional programming. Jan 85.179.23.127 (talk) 23:40, 27 June 2008 (UTC)
- The reason for clipping the spectrum at some point, is that the CIE 1931 data has a bad resolution for the less visible wavelengths. Light with wavelengths abouve 690nm needs more than 100 times of the energy of light with 555nm appearing same bright [3]. As the table contains only sRGB colors with maximum chroma (to get as close as possible to the true spectral color), using the wavelengths at the border of the visible spectrums would magnify the errors of the CIE 1931 data. Jan 85.179.23.127 (talk) 09:08, 28 June 2008 (UTC)
I've found another page, which is dealing with rendering of the visible spectrum in sRGB: http://mintaka.sdsu.edu/GF/explain/optics/rendering.html Jan 85.179.0.13 (talk) 22:12, 27 June 2008 (UTC)
- Interesting. At least he explains the pros and cons of various approaches, although all his diagrams show artifacts at the pure R/G/B primaries, but that could have to do with my current laptop monitor. I still don't agree with mixing in B into R to simulate deep red. At my job, I regularly deal with 800 nm light (and occasionally a 675 nm laser pointer) and they don't look purple/pink. Han-Kwang (t) 23:17, 27 June 2008 (UTC)
- In the discussion page for the color article I explained the reason why to use blue to create the impression of red with a longer wavelength than the sRGB primary red. However using this method reduces the chroma of the color. A line drawn from the spectral color with 700nm to the D65 white point in the CIE 1931 xy diagram will cross the purple line of sRGB. Expanding the hue from the point of the pure sRGB primary to the longer wavelengths leads to a wrong display of hue. I think it's better to make an error in chroma than making an error in hue, especially because with any RGB system (consisting of non-imaginary colors) you always have to reduce the chroma for most colors (especially for cyan or yellow, depending on the position of the green primary), but it's possible to give a correct representation of the hue for all colors (assuming displays and humans are working according to the standards ;-). Jan 85.179.23.127 (talk) 08:52, 28 June 2008 (UTC) and 85.179.23.127 (talk) 11:25, 28 June 2008 (UTC)
- I used a color picking tool on best_spectrum.jpg to determine the color of approx. 630nm and got #fe0046 as result. As #xx0000 red is often used in programs/documents, perhaps you can get used to the "orangish" sRGB-red while working on the computer, and get the impression that #ff0055 is too purplish. Also my monitor is not calibrated and the color appearing on my (consumer) LCD display varies depending on the viewing angle. Jan 85.179.23.127 (talk) 23:31, 27 June 2008 (UTC)
The problem with the magnetkern.de site's approach is that it ignores the Abney effect, projecting the intended hue along straight lines toward the white point. Subjectively, this is bad; the actual curves of constant perceptual hue would map pure reds to pretty near the sRGB primary; if any blue is needed to counter the orange, it's not nearly as much as these guys used based on straight lines. Here is a better book source and diagram. Dicklyon (talk) 17:27, 28 June 2008 (UTC)
- Do you know how to calculate the quantitative impact of this effect? There are a lot of other effects on color perception too. To take all of them into account, one would have to know the exact viewing environment (ambient light, size of the area, background color, absolute luminance, etc...). My program is also capable of using the CIECAM02 color appearance model for compensating many of that effects (that is one reason why it's so long), but I'm not sure, if the Abney effect is taken into account by CIECAM02, and if it's worth making the mechanism more complicated (and therefore less verifyable). I guess that would depend on the quantity of the impact. Another thing I would like to note, is that this problem is not limited to colors for wavelengths greather than 610nm, so just clipping at the edge of the gamut does not solve the problem, but makes it just less noticable. Jan 85.179.23.127 (talk) 17:48, 28 June 2008 (UTC)
- I don't have a quantitative formulation of the effect. I don't think CIECAM includes it either. What's seems clear is that you don't improve the hue of the red and blue primaries as representations of extreme wavelengths by adding some of the other; in both cases, you get a purple perception (OK, maybe a little could help, esp. on the violet end). The reason it's not much of an issue at other wavelengths is that nobody has a calibrated wavelength-to-hue perception; it's only when you get into the extra-spectral colors by mixing red and blue that it looks wrong. Dicklyon (talk) 18:27, 28 June 2008 (UTC)
- So I think as long as I don't have any quantitative information, I would not like to make "manual" adjustments on my own. But if you are right, then probably the (subjective) limit between red and orange might be really above 610nm. But I still think that 630nm (as shown in the Color article) is too high, as there are some LEDs sold with 625nm as peak wavelength (for example by Reichelt Elektronik, order code LED 5MM 2MA RT, german page, but english datasheet is online available), which would have to look orange then (as the wavelengths shorter than the peak wavelength would turn the color more yellowish and the wavelenghts longer than the peak wavelength would not compensate that effect). Jan 85.179.23.127 (talk) 18:46, 28 June 2008 (UTC)
- I agree that 630 is too long for the orange–red boundary. The only reason it's there is because that's the only accessible book source I could find; look for an alternative better source and we can change it. What I wanted to avoid though is making up unsourced numbers. Similarly, the pages of sRGB equivalents to wavelengths is essentially unsourced WP:OR. If we can find a WP:RS, we should include such a thing; otherwise not. Dicklyon (talk) 23:33, 28 June 2008 (UTC)
- Is it correct that the source for the 630nm boundary is Craig F. Bohren (2006). Fundamentals of Atmospheric Radiation: An Introduction with 400 Problems. Wiley-VCH. ISBN 3527405038? To me the title looks like the book is not a reference book for colorimetry but dealing with radiation in general, so I'm not sure if I would consider it trustworthy related to color appearance topics, which might not be the main purpose of the book. Jan 85.179.1.70 (talk) 18:19, 29 June 2008 (UTC)
- Yes, it read 625 before I changed it here. I didn't care about the particular numbers so much as tieing the table to a source, since people kept changing them. Find a better source and you can update it. Dicklyon (talk) 18:36, 29 June 2008 (UTC)
- I have read about the vandalism on the Color article, but I didn't knew that sticking to 630nm was related to that. Jan 85.179.1.70 (talk) 19:36, 29 June 2008 (UTC)
- Not vandalism, just many well-intentioned improvement opinions without any sources. Here are some places to look for a good alternative set of numbers. Maybe this one will do. Good luck. Dicklyon (talk) 20:29, 29 June 2008 (UTC)
- Both books and free software may have errors, but compared to a data-table from a book, with an open source program it is at least possible for people to review what happens (though not for all people, I also had a lot of time difficulties reading sources written by others). I included literature references in my program to make it verifyable. If you think that following the references on my page is too complicated, and if you don't want to link to a page, which you don't think is completely verifyable, then you have no other choice than removing the link. But I would also like to note that the second (Green Flashes) page got results very similar to those on magnetkern.de, so in my (probably biased) oppinion it's quite unlikely that both sources are erroneous. However I don't want to question wikipedia policies, I just wanted to provide a handy translation table, which anyone can use. In any case this discussion helped me improving my page, so thank you for the hints! Jan 85.179.1.70 (talk) 18:50, 29 June 2008 (UTC)
- I have added the following notice to my page: "The reduction of chroma corresponds to a mixture of the spectral color with white light (D65, according to sRGB), which may cause a different percieved hue compared to the true spectral color." So now it's more clear how the values were calculated, and that not all effects related to color appearance have been taken into account, as the reduction of chroma was done in a "physical" way, rather than using a more complicated and less well-defined "biological/psychological" way. Jan 85.179.23.127 (talk) 20:06, 28 June 2008 (UTC)
- You should add that the result is that the colors are too purple at both ends due to the Abney effect. Dicklyon (talk) 23:33, 28 June 2008 (UTC)
- You finally convinced me, that the appearance effects should not be ignored. I modified my program to use both ways of increasing/reducing chroma: "physical" mixture with white light and/or using a color appearance model to map saturated sRGB colors to almost monochromatic colors (only 1% white) while keeping the perceived hue constant. I like to use the CIECAM02 model, because according to the book "Color Appearance Models" from Mark D. Fairchild (2005) the CIECAM02 and the Hunt model are the best choices: "[...], if further sophistication is required, CIECAM02 would be the best choice. Lastly, if CIECAM02 is not adequate for the given situation[...], then the Hunt model would be the most comprehensive choice". However he also states that the Hunt model is rather complex: "Its complexity makes application of the Hunt model to practical situations range from difficult to impossibe." There have been two reasons for using a 99% saturated color, instead of a 100% saturated color: First working on the absolut limit can induce numerical calculation errors and second it also conforms to real life, as a screen reflecting a laser always reflects a bit of white surrounding light too (unless being in a complete dark room). As I stated on my page too, the choice which color appearance model to use is not prescribed by the sRGB standard but has to be done by considerations of the properties of the existent models. I updated my page to mention the advantages and disadvantages of the two approaches, and to list the results of both calculations. I was surprised about the impact of the previously non-considered effects: "Deep red" now is mapped to #ff002c instead of #ff0055 (according to the prediction of Dicklyon, that less blue was neccessary than I used before). But also in the middle of the spectrum you can notice the differences: With physical chroma reduction #00ff6c would correspond to 542 nm, and using CIECAM02 #00ff6c corresponds to 530 nm. Jan 85.179.1.70 (talk) 14:29, 29 June 2008 (UTC)
Btw, some time ago, before this discussion started and before I created the mapping table, I looked incidentally at an alarm clock in a dark room, which had a 7-segment LED display, and I was surprised how "deep red" it looked like. I was thinking that the computer red looks more orange than this LED display. This was of course just my personal impression. It was probably using a GaAlAs semiconductor with 660nm peak wavelength (also shown in the datasheet I referred to above). Jan 85.179.23.127 (talk) 18:56, 28 June 2008 (UTC)
- Yes, 660 nm is going to be about the deepest red you can get. Longer wavelengths just get dimmer, continuing to stimulate only the L cones. Which brings up my theory of "campfire vision": when you sit around a campfire, after the flames are gone and it's all red and orange, the radiation is stimulating a mixture of rods and L cones mostly, and depending on where you look, in, near, or away from the fire (and some M cones when you look right at the orange parts). You get a strange sort of 2D color space, like you're somewhat color blind, but not along the usual opponent dimensions. Has anyone looked into something like this? Dicklyon (talk) 23:33, 28 June 2008 (UTC)
- I think it's the same effect you notice when using a colored light for illumination (i.e. an orange LED cluster). Jan 85.179.1.70 (talk) 14:45, 29 June 2008 (UTC)
- Colored light, maybe, but LED, no. You need a broad enough spectrum for this effect, I think, such that you get some color; a single narrow LED won't do that. Dicklyon (talk) 15:36, 29 June 2008 (UTC)
- Yes you are right, probably an LED might be too narrow, though LEDs are not completely monochromatic. Jan 85.179.1.70 (talk) 17:06, 29 June 2008 (UTC)
Using the most authoritative sources you can find (CIE and W3C/sRGB), I was able to show with a single matrix multiplication that the image from Han-Kwang is either wrong or contains non-documented perceptual compensations (unless someone can show where and how the compensation is done, see above). It is also quite questionable that the 630nm "boundary" on the Color article between red and orange is correct, as Dicklyon already confirmed. I can understand wanting to keep the wavelength table in the color article stable (i.e. based on "trustworthy" books), even if we know one value is wrong. I also don't see any reason to remove the image of Han-Kwang, because it still gives a very good overall impression of the wavelengths of the visible spectrum. And I did not see any verifyable argument that the content of my page is wrong, except for the correct objection from Dicklyon related to perceptual effects, which are now taken into account on the page, while mentioning both the advantages and disadvantages. The page does not claim to be more authoritative than it is: "The calculations were done using a self-written program. The source code contains references to literature for the used constants and equitations." I'd like to hear your comments. Jan 85.179.4.11 (talk) 13:25, 1 July 2008 (UTC)
| This is an archive of past discussions about Wavelength. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. |
| Archive 1 | Archive 2 | Archive 3 | → | Archive 5 |


