Talk:Real projective line

The main image with the circle

The main image looks something like a circle with one point representing both negative and positive infinity. I find this image confusing. I picture the real projective line as a real line with two added points, Inf and -Inf. An even better picture in my mind I get is just the real number line and two added dots. Is this image misleading or not? I don't have any reference texts beside me to cite at the moment, sorry. 137.124.161.17 (talk) 00:19, 26 January 2016 (UTC)

There is only one point at infinity on the projective line. You're perhaps thinking of the extended real line. Sławomir
Biały 01:07, 26 January 2016 (UTC)

Ah, alright. thanks. I got them confused for a second. Why is there a circle. Sorry, still haven't gotten any reference texts. I'm too lazy to walk upstairs and check out the needed books, lmao. 137.124.161.17 (talk) 02:20, 26 January 2016 (UTC)

redundant articles

There are articles on projectively extended real line and projective line that overlap severely with this one. The first could probably be eliminated and seems to be a WP:FORK. Possibly merge all three. 73.89.25.252 (talk) 23:18, 15 June 2020 (UTC)

It is true that the projectively extended real line is a real projective line, but the converse is wrong. In particular, the projectively extended real line is a number system, which real projective lines are generally not. In particular, there is an arithmetic on the projectively extended real line ($1/0=\infty$) that does not extend to other real projective lines. So, these two articles are about two related topics, none being a subtopic of the other. Moreover, the intended audience of these two article is completely different. So, there is no reason for merging them.

On the other hand, the only part of Real projective line that is specific to the real case, is the manifold structure (one single section). So, I would not oppose to a merge with Projective line, if the merged article remains accessible for readers who know real numbers but not general fields. D.Lazard (talk) 07:18, 16 June 2020 (UTC)

That article on "a" real projective line uses the "a" form in the first paragraph only (2 times) and "the real projective line" in the rest of the article (16 times).

You seem to be speaking of a canonized P^1(R) ("the" proj line, qua number system) that non-canonically coordinatizes all other lines ("a" line) in projective geometry. If so then the names should match the same dichotomy in the non-projective case: real number system and real number line versus geometric lines in real (Euclidean, affine, or vector) space. The analogue would be "projectivized (real) numbers" or "projective (real) number line" for the coordinate system and lines in projective geometry (or projective extension of affine lines).

P^1 as a number system is questionable. Does anyone refer to it as such? I have never heard any extension of rational functions to the one-point compactification described as a calculation in P^1 considered as an algebraic structure or a number system. P^1 is in such cases considered as an extension of the domain or range of the function, not as an expansion of the number system. 73.89.25.252 (talk) 06:55, 17 June 2020 (UTC)

There is a natural left action of PGL₂(R) on P¹(R)

The group GL₂(R) acts on the left on the space of column vectors R² by matrix multiplication. In this way, each matrix A defines a function f_A from R² to R². If B is another matrix, then $f_{A}\circ f_{B}=f_{AB}$ because $f_{A}(f_{B}(v))=f_{A}(Bv)=A(Bv)=(AB)v=f_{AB}(v)$ holds for all column vectors $v\in \mathbf {R} ^{2}$. Thus matrix multiplication is compatible with composition, when one uses the left action on column vectors. The same then follows for the induced left action of PGL₂(R) on P¹(R).

Indeed, it is this left action on P¹(R), with ${\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ acting as $x\mapsto (ax+b)/(cx+d)$, that one finds in standard references such as

• Serre, A course in arithmetic, VII.1.1.
• Miyake, Modular forms, §1.1.
• Lang, Complex analysis, VII, §5.
• Lang, Elliptic functions, 3.§1.
• Stillwell, Mathematics and its history, §8.6.
• Koblitz, Introduction to elliptic curves and modular forms, III.§1.

(Some of these references are over C, but the principle is the same over every field.)

If anyone disagrees with all these authors, can you please explain why and list the published references you are using to support your claim? Thank you, Ebony Jackson (talk) 04:59, 27 December 2020 (UTC)

Due to the transpose involution, the group PSL(R) can also be presented as the opposite group given in the "left action". Practicing geometers like J. W. P. Hirschfeld and Rafael Artzy use row vectors and right action. Look at all the parentheses necessary in the presentation of the opposite group! The carry-over of prefix notation for functions, used in calculus and complex analysis, lets some authors (as listed) use the confusing reverse writing, but this article is about geometry and transformation. The composed transformation AB in a group is usually read in the order written; the "left action" expects B to be applied to the column vector before A is applied, clearly corresponding to the group opposite to what geometers such as Hirschfeld & Artzy prefer. Some readers may need to refer to the contribution of December 27, 2020, about PSL(R) that has been changed. — Rgdboer (talk) 03:10, 30 December 2020 (UTC)

Thank you for your response! I have heard that several decades ago, there was a pocket of mathematicians in the U.K. who started writing functions to the right of their arguments, so that to apply the composition f∘g one would apply f first and g second, as you mention. But it was a losing battle, and I think that essentially all of them abandoned that notation. Even J. W. P. Hirschfeld, it seems, now writes his transformations on projective space using matrices acting on the left: see p. 4 of his 2008 book Algebraic curves over a finite field. And Rafael Artzy seems to have passed away in 2006, so one can hardly call him a practicing geometer.

Writing functions to the left of their arguments is the standard in virtually all of mathematics, not just calculus and complex analysis, and this includes almost all branches of geometry as well. The vast majority of users of the projective line will be more familiar with this standard convention. If you still feel it is worth mentioning that there is a convention in which transformations are written on the right, this could be done in a note with a citation to a book that uses this convention, but I feel that it would be wrong to present this convention in the main text as if it were standard in the 21st century.

By the way, by PSL(R) do you mean PSL₂(R) = SL₂(R)/{±1}? That group is not the full group of linear automorphisms of P¹(R). Ebony Jackson (talk) 04:50, 30 December 2020 (UTC)

Functions are a type of binary relation. The representation of functions in the calculus of relations puts some context to this discussion. In particular, composition of relations turns the tables on the prefix notation, making it the out-dated scheme. Some practice in this more general context leads to an appreciation of the clarity provided by right action. — Rgdboer (talk) 05:25, 31 December 2020 (UTC)

Almost all mathematics is built up on the convention that in a composition of functions,$f\circ g,$ the function g is applied first, that is, $(f\circ g)(x)=f(g(x)).$ It is for complying with this convention that the matrix multiplication is defined by combining rows of the first matrix with columns of the second matrix, and that the matrix representation of a coordinate vector is a column matrix. Historically, these conventions, and several others, took some time for being elaborated in a coherent way. An example of survival of older conventions is Sylvester matrix, where the Sylvester matrix is written as the transpose of the matrix of the corresponding linear map. It is possible to choose the opposite convention, but coherency would imply to change all related conventions, and therefore to change accordingly almost all mathematical articles. It is certainly not the role of Wikipedia to promote such a dramatic change.

It is possible that in some specific areas of mathematics (possibly the theory of relations), with few interaction with the main stream of mathematics, it is convenient to use a different conversion. But, for being usable in other areas of mathematics, the theorems obtained in such an area (if any) must be translated in the standard convention.

For this reason, Rgdboer's version is not acceptable, and Ebony Jackson's must be kept. However, a confusing point must be clarified, which is the implicit use of $[x:y]$ as a column matrix. I believe that this is the hidden origin of this discussion, and I'll try to clarify this in the article. D.Lazard (talk) 10:57, 31 December 2020 (UTC)

To clarify the choice, see Geometric transformation#Opposite group actions recently contributed. — Rgdboer (talk) 04:29, 3 January 2021 (UTC)

Is image correct?

I tried to find a formula that gives me value for any provided angle. It is a piecewise function that is defined as:
$f(x)={\begin{cases}{\frac {\pi }{-2\pi -2x}},&x\in (-\pi ,-1]\\{\frac {2x}{\pi }},&x\in (-1,1)\\{\frac {\pi }{2\pi -2x}},&x\in [1,\pi )\end{cases}}$
So I have two questions.
1. Do values near dots on a picture represent actual values or are numbers not attached to a particular place and persist only for illustrative purposes?
2. If values are attached to particular places, should they be represented by that formula? Отец Никифор (talk) 15:45, 22 November 2024 (UTC)

The diagram is supposed to be only illustrative. If you want an exact transformation, you should use the stereographic projection (as a one-dimensional function of angle measure, the "half-tangent"). Then 1/2 and 2 will be about 53.1° and 126.9° away from 0, respectively, compared to 1 being 90° away from 0. The appropriate function is: $$f(x)=\tan {\tfrac {1}{2}}x.$$ –jacobolus (t) 23:09, 22 November 2024 (UTC)

Thanks. I thought about tangent as natural way to fit infinite numbers into some range but that one on the picture has very interesting symmetries. I want to know more about that, but looks like it is just illustration without any deep meaning Отец Никифор (talk) 22:49, 23 November 2024 (UTC)

Semicircle model of the real projective line

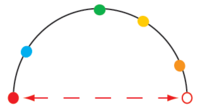
Given that a projective space is formed by identifying antipodal points in a sphere of a Euclidean space of one higher dimension, the semicircle is the natural picture for the real projective line. — Rgdboer (talk) 02:40, 1 December 2024 (UTC)

I find this image misleading. Indeed, in a projective line, all points play the same role, which is the case in the full circle representation, but not in the semicircle model. D.Lazard (talk) 11:29, 1 December 2024 (UTC)