Talk:Group (mathematics)/Archive 3
| This is an archive of past discussions about Group (mathematics). Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. |
| Archive 1 | Archive 2 | Archive 3 | Archive 4 | Archive 5 | → | Archive 8 |
Good article review
- It is well written.
Not yet- For example, the powers of any element a and their inverses (that is, a0 = e, a, a2, a3, a4, …, a−1, a−2, a−3, a−4, …) always form a subgroup of the larger group, the so-called cyclic subgroup generated by a, see below under Cyclic groups. Link "cyclic subgroup" and get rid of the "see below" part. Also, it might be useful to write a1 in the list.
- The operation between the cosets behaves in the nicest[7] way possible: (Ng) • (Nh) = N(gh) for all g and h in G. Move the citation to the end of the sentence.
- "Lie groups" has a one sentence paragraph that should be merged into the one before it
- It is factually accurate and verifiable.
Not fully verified- Try to aim for at least one reference per section. Usually a footnote for the first sentence of each section does the trick.
- It is broad in its coverage.
- Pass
- It is neutral; that is, it represents viewpoints fairly and without bias.
- Pass
- It is stable; that is, it is not the subject of an ongoing edit war or content dispute.
- Pass
- It is illustrated, where possible, by images.
- Pass
Let me know when you're done.-Wafulz (talk) 14:32, 2 May 2008 (UTC)
- Thanks for your review. The issues mentioned above have now been fixed. I believe that adding additional further footnotes would decrease the readability of the article. So, not every single subsection contains a footnote. But I tried to back up every statement which may not be directly clear to the reader. Jakob.scholbach (talk) 18:04, 6 May 2008 (UTC)
- It looks good to me. However, I do combinatorics and number theory by trade, so I'm requesting a second opinion to (hopefully) get someone who has more expertise with this topic. Thanks for your patience.-Wafulz (talk) 12:32, 7 May 2008 (UTC)
- I've been watchlisting this page during the review process. I've made minor contributions during the review, but am not a significant contributor. I have expertise in geometry and am very familiar with undergraduate and some advanced group theory, but also have some experience of the GA process, so I hope I can provide a useful second opinion. The "list/do not list" decision remains with the original reviewier however.
- My main comment is that I think this is an excellent introduction to the concept of a group. It meets the challenge to be broad, accessible and encyclopedic very well. It is also well written and neutral point of view. I list below the problems that I noticed.
- Prose style: generally this is very good in my view, but there are some lapses, and some issues with encyclopedic tone.
First example: the identity element discussion is repetetive. I suggest dropping the first sentence, and clarifying the third, placing "additive" in brackets, as in the inverse element part.Variants of the definition: try to find a better subject for these sentences than "one".Basic concepts in group theory: the first paragraph contains the only really bad prose I have found in the article; please don't start paragraphs with long noun phrases, or use gerunds as subjects of sentences. This paragraph needs a complete rewrite."By counting cosets, one can show Lagrange's theorem...": rephrase with an identifiable subject, preferably in the active tense; one approach would be "Lagrange's theorem, which states..., follows by counting cosets.""Quotient groups, also known as factor groups, form the counterpart to subgroups." This conveys no meaning to the reader who does not already know what it means.What it is the relation between subgroups and presentations?Simple groups: the second definition appears to include the trivial group, whereas the first does not.(Good solution!)Group homomorphisms: "Groups together with their morphisms are assembled in the category of groups." This is not properly explained (what is a morphism?) and the prose is weak.Cyclic groups: why the need to assemble them into a set?Order of a group: o(a) is a common notation for the order of an element.Notations: "Groups can use different notation...". Please fix. I could probably fix this one myself, but I'm not completely sure what you are trying to say. A lot of the prose in this section needs improvement.In general try to avoid the use of "we" and "one": sometimes using these words is the best option, but often one/we can find a better subject for the sentence :-)
Citations: the scientific citation guidelines (a GA requirement) encourage providing one general citation per section so that the reader knows that the material is general knowledge and where to find it. I fail to see how this would diminish the readability. In the first section, a citation for the particular form of the axioms chosen would be reassuring (in particular, the "closure" issue). The second section would benefit from a general reference and a reference to a book on group representation theory. As mentioned above, the first paragraph of "Basic concepts in group theory" needs to be rewritten: I suggest taking the inspiration from a source and citing it. The "Notations" section is a bit weak and so really needs a source. In the generalizations section, I would think references are needed to cover each and all of the generalizations presented.- Images and tables: these need captions.
In particular, the parenthetic aside on the coloring of the vertices of the square would be much more use as part of a caption for the image. The group table of d4/8 could use a caption as well, to explain the shading.(Captions could be improved, but are okay.) - The lead.
The lead fails to summarize the article because it does not refer at all to any of the material described in the "Basic concepts in group theory" section. - There are one or two other broadness issues, but I think the above is already too much food for thought!
- Taking this forward to FA. There are lots of MoS issues that need to be fixed, e.g., em-dashes are now required to be unspaced (much to my regret). There is also a question of comprehensiveness. I suggest developing the Group theory article to GA first. This article reads a bit like an Introduction to group theory article. A comprehensive article on groups and/or group theory could/should include a lot of advanced material. Lie groups and representation theory, for example, get fairly short shrift here. Geometry guy 20:41, 8 May 2008 (UTC)
- Prose style: generally this is very good in my view, but there are some lapses, and some issues with encyclopedic tone.
(←) Most of my comments have been addressed: sorry to be a bit slow striking them. Please note that the fact that not all comments have been striked does not mean I oppose the listing of this article as GA. Editors here have done fantastic work. My only hesitation is the applications issue raised below. While I accept that the hatnote defers applications to the group theory article, I still have broadness concerns here. The ideal would be a separate article on Applications of group theory with a summary style section in Group theory and a shorter summary style section in this article. For instance, quantum theory (both quantum mechanics and quantum field theory) relies on the notion of a group in quite a foundational way.
I think this is a GA issue because the last paragraph of the lead is not fully developed in the article. Furthermore, a couple of references to applications in the body of the article do actually need citations, because they involve statements of opinion on the importance of group theory: the "important role" and "pivotal role" sentences on Lie groups. These viewpoints are widely agreed, so a cite should be easy to find.
I remain impressed by the work that has gone into this article, and its balance and tone. I think it will still have a hard time at FAC, but I am willing to help out in support of the dedicated contributors. The remaining GA issues I have are pretty minor. Geometry guy 19:08, 14 May 2008 (UTC)
Issues raised by Geometry guy
Prose style
- I believe I have addressed the majority of the bulleted points for 1.
- Basic concepts intro should be looked at: no reason the new must be better than the old.
- Relationship between presentations and subgroups (is amazingly interesting, but) has not been made clearer. The editor just mean the normal subgroup generated by the relations... is a subgroup.
- For simple groups, I think generally the trivial group is not called simple, but I think it is important to remember "who cares", and so have phrased the definition to technically exclude the trivial group from the definition, by refusing to address it. I believe this is a common method.
Category theory prose is still weak, but at least the only new word is blue linked now. This is basically a "see also" stuck into the text.fixed by the other leading JS.Notations has not been changed. It is unclear how useful it is in an encyclopedia, rather than in a textbook. I am not sure how to phrase its waffling statements more strongly.ditto.We should be careful how often one is distracted by change in voice, but I have not done anything about it.ditto
- Thanks again for the two detailed reviews. JackSchmidt (talk) 21:39, 8 May 2008 (UTC) and updated 20:59, 12 May 2008 (UTC)
- I believe I have addressed the majority of the bulleted points for 1.
- First example: the identity element discussion: done Jakob.scholbach (talk) 13:58, 9 May 2008 (UTC)
- "We" and "one": I eliminated every occurence (in one place (Quotient groups) I wasn't sure what to take else) and tried to get directly to the point of the phrase in question. Hopefully an improvement.... Jakob.scholbach (talk) 19:29, 9 May 2008 (UTC)
- This is not a matter of principle: we/one can be better than an awkward passive construction and is certainly not forbidden, but often looking for a good subject for each sentence leads to better prose. Geometry guy 20:05, 9 May 2008 (UTC)
- Lagranges theorem...: this is now reformulated (and moved to finite groups).
- Notations: this is now much shorter (I eliminated some less important stuff + redundancy). Hopefully also better structured. One citation still missing. Jakob.scholbach (talk) 19:56, 12 May 2008 (UTC)
- I believe this section (prose, #1) is now done. JackSchmidt (talk) 20:59, 13 May 2008 (UTC)
Citations
- I have added a general reference for all of the "examples" subsections except the integers (under + and *). Jakob.scholbach (talk) 11:08, 9 May 2008 (UTC)
- I haven't yet checked this carefully, but a cite for the axioms presented is still missing. Do you agree that this is worth providing? Geometry guy 20:05, 9 May 2008 (UTC)
- Yes, I agree. I had a somewhat different idea earlier, namely that almost all of the content is covered in almost every book in the ref list. But you are perfectly right. At the moment, I don't have access to books, but as soon as I do, I will try to cover the rest of the sections still missing a reference. Or, obviously, if somebody is faster ... Jakob.scholbach (talk) 20:25, 9 May 2008 (UTC)
- Now, every section except "Division" and "First example - the integers" contains at least one general reference. I hope this is enough. Jakob.scholbach (talk) 15:01, 13 May 2008 (UTC)
- The newly added section about symmetry groups (this article is a mess, btw) now needs a general reference. Jakob.scholbach (talk) 21:03, 13 May 2008 (UTC)
Images and tables
- I added two captions. I don't know how to get nicer formatting, though. Any formatting experts in the house? Jakob.scholbach (talk) 14:12, 9 May 2008 (UTC)
- I have been happy with the formatting. I don't like lots BR tags captions. I have to use larger font sizes than many editors, so the margins for me are different than for the anonymous uebermenschen browsers with perfect eyesight. Captions with lots of BRs and such just look ragged to me. The position on the page also looks fine to me. Were there any in particular you were worried about? JackSchmidt (talk) 20:51, 12 May 2008 (UTC)
- I wasn't exactly happy with the BR tags, too. I introduced them because without them the table gets very large (as to display the whole caption in one line). I wasn't able to circumvent this behaviour. The caption not wrap automatically into several lines. Jakob.scholbach (talk) 13:09, 13 May 2008 (UTC)
- I fixed the column widths to the width of the (current) pictures. Now, the captions wrap natural without the need of BR tags. Yeah. (TimothyRias (talk) 13:41, 13 May 2008 (UTC))
- I wasn't exactly happy with the BR tags, too. I introduced them because without them the table gets very large (as to display the whole caption in one line). I wasn't able to circumvent this behaviour. The caption not wrap automatically into several lines. Jakob.scholbach (talk) 13:09, 13 May 2008 (UTC)
Lead section
- I tried to improve the lead. Contentwise it's now closer. But my limited English abilities prevent me from more brilliant prose... Jakob.scholbach (talk) 20:03, 9 May 2008 (UTC)
- It looks good to me as well. I think anything too brilliant detracts from the article. An encyclopedia article should catch the interest of the reader, but not try to dazzle them or anything. Otherwise, we should have some sort of flash image of a tiger leaping out of one of the early illustrations, hopefully roaring something that sounds like "grrrrrroups", and then the screen fades away to "behold its fearful symmetry!" JackSchmidt (talk) 20:55, 12 May 2008 (UTC)
- You seem to have a lot of unused creative energy :-). Perhaps you are up to writing a comic like the ones on WP:POST? OK, then let's consider this issue fixed for now. Jakob.scholbach (talk) 13:10, 13 May 2008 (UTC)
- It looks good to me as well. I think anything too brilliant detracts from the article. An encyclopedia article should catch the interest of the reader, but not try to dazzle them or anything. Otherwise, we should have some sort of flash image of a tiger leaping out of one of the early illustrations, hopefully roaring something that sounds like "grrrrrroups", and then the screen fades away to "behold its fearful symmetry!" JackSchmidt (talk) 20:55, 12 May 2008 (UTC)
Broadness issues
- GGuy, could you please give a hint what you'd like to see here? Jakob.scholbach (talk) 20:04, 9 May 2008 (UTC)
- Sure. By and large, I think this article is probably broad enough for GA, which is one reason I didn't detail. Another reason is the overlap with the still-to-be-well-developed Group theory article. At the FA level, "broadness" is replaced by "comprehensiveness", and it is probably easier to say what is needed in a comprehensive article than a broad one. Here are a few issues.
- Apart from the discussion of the classification of finite simple groups, the article barely touches upon advances in group theory made in the last 50 years. Maybe that is the job of the Group theory article, but some advances probably deserve a mention. One example is computational group theory, and computer algebra (there is a hint of this at List of small groups). Another example, already mentioned, is group representation theory (especially Lie groups). It is also worthwhile to tell the reader that this is work in progress (one of the common questions asked of mathematicians by lay folk is "I thought it was all known"/"what is more to prove?")
- A related issue is the absense of any history: again this is covered by the group theory article, and so is probably not required at GA level for this article, but an introductory article to groups would certainly be enhanced by an introduction to the colourful history of the subject.
- There is no section on applications. My feeling is that this really is a GA-broadness issue. Groups are fundamental in physics. The article mentions this in the (old and new) lead, but fails to elaborate it in the article. Such an applications section is vital, in my view.
- I hope that helps. Again, I emphasise that you should trust your own judgement: I have the impression that at least one regular editor here is a real expert on group theory. Make this article sing and leave it to the judgement of the main reviewer to assess whether the article is GA. Geometry guy 21:02, 9 May 2008 (UTC)
- Sure. By and large, I think this article is probably broad enough for GA, which is one reason I didn't detail. Another reason is the overlap with the still-to-be-well-developed Group theory article. At the FA level, "broadness" is replaced by "comprehensiveness", and it is probably easier to say what is needed in a comprehensive article than a broad one. Here are a few issues.
- Applications: I can think of only one type of application that fits in the current article, but it should be sufficient. It is summed up as "symmetry is good for science".
- Highly symmetric block designs save money: You don't want to test your expensive new drug on everyone, but you know your population is multidimensional, how can you eliminate correlation in multiple dimensions with small sample sizes?
- Highly symmetric subsets of vector spaces like Golay codes.
- and then the only one which is "worked":
- Symmetry saves time: if you need to count something and a group acts on it, count orbit sizes instead. How many distinct rearrangements of MISSISSIPPI are there? How many colorings of a necklace? I intended for this to be at the level covered in very basic classes on counting, perhaps for ages 15 to 20.
- If someone wants to add these feel free. I don't have the references handy, but most discrete math books should have something like this. Most of the good applications I know require a little more than is covered in this article. JackSchmidt (talk) 20:46, 12 May 2008 (UTC)
- Applications: I can think of only one type of application that fits in the current article, but it should be sufficient. It is summed up as "symmetry is good for science".
- OK. We have some (very short) glimpses of applications (cryptography for finite gps, molecular symmetries and physical theories for Lie groups, and gauge theory and error corrections for finite symmetry groups). I think this should be enough for a "good" article. This belief is also based on the idea, that in fact one is not really applying groups (which are abstract in a sense), but group theory (the knowledge about groups, so to say). This, and the idea that group theory shall contain (and already contains) more application material, make me think this way. Jakob.scholbach (talk) 15:01, 14 May 2008 (UTC)
Conclusion
I think we have covered all points in the reviews above. If nobody is against, I will probably ask Wafulz, the first reviewer (of the 2nd review) to give his opinion, or if he doesnot want to decide, we probably need a 3rd opinion... Jakob.scholbach (talk) 15:03, 14 May 2008 (UTC)
- In my opinion, you've met the Good Article criteria, so I'm promoting the article. For "next steps", I suggest you go for a peer review and maybe aim for FA. Congrats and thanks for your hard work.-Wafulz (talk) 18:59, 14 May 2008 (UTC)
Rational number example in first section
I couldn't find when this example was added to the first section, but its addition is unnecessary and, in my opinion, undesirable. Someone went to a lot of trouble to explain the idea of a group in terms of symmetries using those colored diagrams, and this is way better than the rational numbers example, which is too technical for this article (at least that high up in it anyway). I propose completely deleting this reference. Xantharius (talk) 19:02, 6 May 2008 (UTC)
- I added it after I saw it in group theory, in preparation to making this article a subarticle of the other one. In my opinion the example (or a similar one) is essential to this article:
- Groups are algebra, and algebra is just generalised numbers. If we don't give an example with numbers very early in the article, many non-mathematicians who try to read it and have some half-knowledge will be very confused. (It might even make sense to extend this into another example section. Proving the associativity of matrix addition is probably just the right level of abstraction and mathematical sophistication for most of our readers. But then this could detract from the nice square symmetries example, and I agree that that would be a pity. And such arguments would be even more appropriate in field (mathematics) anyway.) --Hans Adler (talk) 19:28, 6 May 2008 (UTC)
- I think the current rational number example is short, to the point, and gives someone (horribly atypical) examples of groups to give them some comfort. So I think the example should stay (I am fine changing "rational" to "real" or whatever people think most readers assume "number" means).
- I did want to mention my strong disagreement with the idea that groups are generalized numbers. Numbers, ordered tuples of numbers, simplicies, finite geometries, manifolds, abstract elements of sets -- these are the passive carriers for group actions, the setting. The groups are the actors. The symmetry example is reasonable as it distinguishes the setting (the square) from the actor (the group). Aschbacher's and Alperin and Bell's textbooks present groups in this light. The next example after symmetry of a shape (a geometric object), should be symmetry of a vector space (an algebraic object), also known as GL. Perhaps another typical example would be the symmetry group of an infinite binary tree. JackSchmidt (talk) 19:55, 6 May 2008 (UTC)
- I still disagree. What groups are fundamentally about is symmetry: their very formulation deals with the nature of symmetry, and groups are the perfect vehicle for describing how symmetries operate on other objects. To have the example of rational (or real) numbers appearing before the beautifully done and accessible example of the symmetries of the square might be appealing to some mathematicians (not this one), but I think for most readers the rational numbers without zero under multiplication is a horrible introduction of the idea of group. By all means have some of these examples later, but not before this very well thought-out presentation of the idea behind groups: that they are about symmetry. I still propose removing this example from its place before the symmetries of the square (particularly in light of it being borrowed from group theory, which is a much more technical article on groups). Xantharius (talk) 20:06, 6 May 2008 (UTC)
- The numbers example is needed for a certain type of non-technical readers (for their "comfort", as JackSchmidt put it, and I agree with that formulation), because otherwise they will never read the beautiful example. Yes, of course groups are mainly about symmetries. We have to pick our readers up where they are (that's a German idiom; don't know if it works in English), and some of them are precisely there, at the numbers. Once we are holding their hands we can take them elsewhere. Especially after seeing multiplication signs and 1s, and reading about "associativity", people expect to see numbers. They are not going to scroll down several pages to understand where the notation comes from. So it will be completely abstract and meaningless for them, and there is nothing more scary for the general reader than abstract notations. --Hans Adler (talk) 20:17, 6 May 2008 (UTC)
- I still disagree. What groups are fundamentally about is symmetry: their very formulation deals with the nature of symmetry, and groups are the perfect vehicle for describing how symmetries operate on other objects. To have the example of rational (or real) numbers appearing before the beautifully done and accessible example of the symmetries of the square might be appealing to some mathematicians (not this one), but I think for most readers the rational numbers without zero under multiplication is a horrible introduction of the idea of group. By all means have some of these examples later, but not before this very well thought-out presentation of the idea behind groups: that they are about symmetry. I still propose removing this example from its place before the symmetries of the square (particularly in light of it being borrowed from group theory, which is a much more technical article on groups). Xantharius (talk) 20:06, 6 May 2008 (UTC)
- It's important to give a familiar example of a group up front, but I actually think a better example is the integers with addition. I suggest something like this:
- A familiar example of a group is set of all integers Z, where the operation • is addition (+). It satisfies these four axioms because:
- The sum of any two integers is an integer.
- Addition of integers is associative.
- Zero is the identity element, since adding zero to an integer always yields the same integer (e.g. 2 + 0 = 2).
- The inverse of an integer is its negative, since adding a number to its negative always gives the identity element, zero (e.g. 2 + (−2) = 0).
- A familiar example of a group is set of all integers Z, where the operation • is addition (+). It satisfies these four axioms because:
- I agree that groups are more fundamentally about symmetry, but before exploring how abstract groups can get it's good to ground it in something familiar and concrete. Dcoetzee 20:21, 6 May 2008 (UTC)
(e/c) If the idea is to give a completely easy "throwaway" example, then why not use the integers under addition? At least this is of fundamental importance as an abelian group, and doesn't require excluding any elements (like zero for the rationals). The rationals under multiplication seem to me to be both atypical and fussy as a first example of a group. silly rabbit (talk) 20:26, 6 May 2008 (UTC)
- Integers under addition sounds good to me. Every torsion-free group has it as a subgroup, so I would be hard pressed to call it absolutely atypical. It certainly should be familiar to readers: I think integers are covered by the age of 12 years old even in slower math programs. It is certainly fundamental to abelian groups, which perhaps my viewpoint is biased against. It will also be *even shorter* than the rational numbers example. Even with the numbered list, the ideas are so clear, that in some sense the example is not there: it is just restating the definition in a comfortable language.
- (to Xantharius) I hope it is clear we agree that groups are fundamentally about symmetry, and our only disagreement is whether a "comfortable" example is worthwhile even if it does not display the idea of symmetry. I think such a simple example is worthwhile (especially the integers), even though it does not express this important idea. JackSchmidt (talk) 20:42, 6 May 2008 (UTC)
Integers are fine for me, too. --Hans Adler (talk) 21:02, 6 May 2008 (UTC)
- OK, why don't we make something like: Definition, First Example, Second Example? In the first example subsection, I'd like to have the fact stressed that Z is a very special group. There would be no notion of group if everything was as simple as Z. Who's up to it? I'm done for today...Jakob.scholbach (talk) 21:34, 6 May 2008 (UTC)
- I've taken a shot at implementing your suggestion. Please edit my rough addition mercilessly ;-) silly rabbit (talk) 22:01, 6 May 2008 (UTC)
- I like it. Would it be too silly to include the "e.g."s? Something like:
- 2 + 3 = 5 is an integer.
- (2 + 3) + 4 = 5 + 4 = 9 = 2 + 7 = 2 + (3 + 4)
- 2 + 0 = 2
- 2 + (-2) = 0
- If we only use letters, then suddenly it is *algebra* and we lose the "even a 10 year old will understand". JackSchmidt (talk) 22:05, 6 May 2008 (UTC)
- I like it. Would it be too silly to include the "e.g."s? Something like:
- Integers under addition sounds like a good plan! If e.g.'s are done, care must be taken not to lose the encyclopedic tone: we aren't writing a textbook here :-) Geometry guy 22:41, 6 May 2008 (UTC)
section headers
Two ideas about sections headers: - "First Example" and "Second example" (suggested by myself) are not terribly informative. How about "Integers -- an everyday group: integers" and "Worked example -- a symmetry group"? - secondly, is it possible to hide some sections from the table of contents? I'd like to hide the third-level subsubsections. They just clutter up the toc, I think.
Comments? Jakob.scholbach (talk) 17:17, 8 May 2008 (UTC)
- {{TOClimit}} added.
- First example: the integers
- Worked example: a symmetry group
- perhaps sounds better? Headings should be short. I think "first example" is a known phrase, meaning the easiest, most everyday example that is worth mentioning. "Second example" might sound silly, I agree. "Worked example" should catch the student's eye. I think indicating which groups are in the example is a good idea. JackSchmidt (talk) 18:33, 8 May 2008 (UTC)
What do you mean by "worked" example? I think it might be a germanism. To me, "worked" suggests "forces" of "far fetched" which is probably not your intention. (TimothyRias (talk) 08:22, 9 May 2008 (UTC))
- It means "exercise and solution", as in this quote from Schaum's Outlines: "each title typically has introductory explanations of topics, plus many fully-worked examples, and further exercises for the student". Wikipedia actually has an article on this method of teaching, Worked-example effect. "'A worked example is a step-by-step demonstration of how to perform a task or how to solve a problem'", "learners that studied worked examples, performed significantly better than learners who actively solved problems". etc. JackSchmidt (talk) 12:40, 9 May 2008 (UTC)
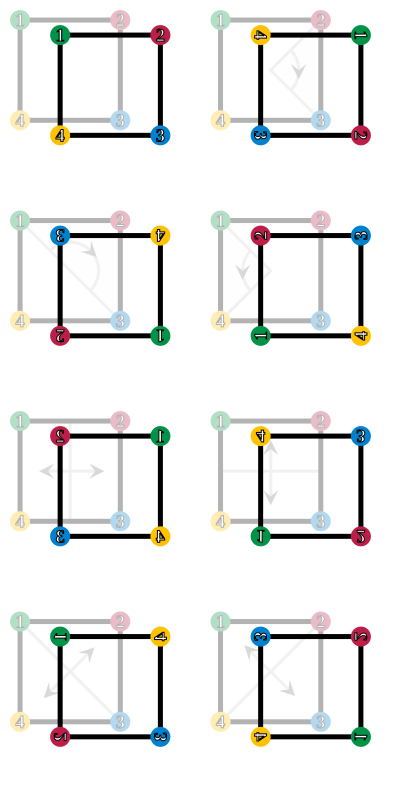
SVG images for the example
I've prepared SVG images for the example, with some minor changes:
Any comments and/or changes that need to be implemented? (TimothyRias (talk) 13:49, 9 May 2008 (UTC))
- For easy comparison:
- They should probably be split for easy captioning. I can't tell if the arrows look really good or really confusing. On the one hand, the colored dots show the result of the action, but the arrows show (to my mind) what the action will do. For instance the bottom left picture says that you should take the red in the top left corner to the green in the bottom left corner, but really what it means is take the red in the top right corner to the green in the top left corner.
- If making these images is easy, would you make some similar to the current "double" images in the article so that it is easier to compare? I like your soft gray and large arrows better, but superimposing the action and the result confuses me.
- Would it be possible to catch the group elements "in the act" like the rubik's cube picture? Maybe each group element gets two pictures, the first is the result of applying 1/3 of the action (in R^3 or SO(3)), with your soft gray arrows to indicate what is happening, and the second is the plain old result. JackSchmidt (talk) 14:08, 9 May 2008 (UTC)
- I also find it a bit distracting to join the operation and the result. I do like the shapes of the arrows. I prefer the colors I chose (they are from User:KSmrq's page, somehow supposed to be perfectly opposite). Jakob.scholbach (talk) 14:15, 9 May 2008 (UTC)
- Oh, I had not noticed the color change. I like TR's heavier lines for the square's edges, and I like his larger, softer arrows. I think I like KSmrq's colors better, and are definitely for them if they are better for accessibility. However, the primary colors used by TR are very clear to me, and I think both will punish the color blind reader.
- Probably the images are too small, but something I've done in the past when teaching is to put numbers inside the dots, as well as color. I was only trying to assist our color blind printer so that both the web version and the handouts were useful, but this might help readers as well. Of course if they don't fit, no worries. It's not like Hall-Janko graph has labelled its vertices :) JackSchmidt (talk) 14:28, 9 May 2008 (UTC)
I updated the colors. Als splitting the picture is little trouble, I just put them together for this test so that I wouldn't have to upload 8 new pictures for every change I made. But for the final version we should definately have seperate pictures.
Currently, I am looking into over laying (and slightly offseting) the original and the result with the original slightly faded into the background.(TimothyRias (talk) 15:04, 9 May 2008 (UTC))
- New colors definitely look good. I'm looking forward to offset "shadow". It sounds neat. I looked at adding numbers, and noticed you did this in the sanest, nicest way possible, by actually using SVG to apply the group elements. It makes the text look funny, but I can't decide if it is a bad thing or not. Try adding:
<text x="-54" y="-45">1</text>
<text x="46" y="-45">2</text>
<text x="46" y="55">3</text>
<text x="-54" y="55">4</text>
- to the id="square" guy. The numbers themselves get rotated and flipped, which looking at it again, looks awesome to me. I don't know how to tell SVG that I want text centered, but at least on my computer the numbers are basically perfectly centered. I suspect it is browser dependent though. Sorry, I don't know much about uploading images to wikipedia. JackSchmidt (talk) 15:19, 9 May 2008 (UTC)
- Oh, and if we have the numbers in there, then it makes it easy to talk about the permutation representation, expressing D8 as a Sylow 2-subgroup of S4. Maybe one would just use the pictures of two generators in some other article. I think D8 might even have its own article. JackSchmidt (talk) 15:22, 9 May 2008 (UTC)
Shadow rotations:
(Image moved)
The 90 right looks very nice, but 180 and 90 left look akward. I haven't figured out what to do with the flips yet. I also looked at adding the text, but it looks funny for 180 turn. (TimothyRias (talk) 15:44, 9 May 2008 (UTC))
- I tried some stuff. I like the result, but I've no idea if others will. Thanks for producing such sane SVG, btw. I'm sorry if mine is not so sane. Feel free to adjust it as needed.
- The artist formerly known as JackSchmidt (talk) 21:04, 9 May 2008 (UTC)
How about this:
I fixed the horizontal text positioning. The vertical one is still a bit sketchy, but I am confident that it should work on all platforms. (And at the moment wikipedia is passing SVG through rsvg anyway so there is no problem.) (TimothyRias (talk) 14:20, 10 May 2008 (UTC))
- I know it is a lot of fun generating nice SVGs like this, but please bear in mind accessibility issues and the kiss principle (less is more). Geometry guy 14:59, 10 May 2008 (UTC)
- I like the bolder font. I think the changes do help accessibility (the current in-article pictures are useless to color blind). Each of the flips looks nice. I like the numbers to make it less dependent on color. I am quite visually impaired, so I do tend to consider WP:ACCESS. Unfortunately, I think people are so different, and math is so far from mainstream, that deciding exactly what makes something more accessible is hard.
- I tend to think in full page handouts, not tiny little tables. I think the ideal handout would have the stationary, original square with the gray arrows indicating the motion to be performed, then the "in action" version next to it, and then stationary, transformed square. I am not sure what is best in the article. I think some sort of picture is definitely wise.
- Would it be reasonable to mostly use this pictures on a symmetry of the square article (I think one already exists), and just have an excerpt in this article with a link to the full article for full glorious images?
- This might address the KISS concern. JackSchmidt (talk) 15:53, 10 May 2008 (UTC)
- Good points about the colour blind and the numbers. Another option is to use an actual animation rather than these faux animations. But I leave it to other editors to decide what the best compromise is: I only wanted to draw attention to the issue, and am glad to hear that accessibility is being taken into consideration. Geometry guy 17:45, 10 May 2008 (UTC)
- I'm impressed by you guys graphic abilities! The animes are interesting, but (except perhaps for the 90 and 270 deg. rotation) the current version is way easier to digest. One thing I could imagine: the "forefront" square showing the result of the operation stays as it is and the starting-point config is shown in grey and arrows show the movement of the vertices toward their final positions. Jakob.scholbach (talk) 17:56, 12 May 2008 (UTC)
I tried something else. (see above) Maybe, this is a little clearer. (some of the arrows may need tweaking.) (TimothyRias (talk) 21:47, 12 May 2008 (UTC))
- Those are simple, and to my mind, clear. I like them, but we should probably hear from others, as I've more or less liked all of them. JackSchmidt (talk) 01:44, 13 May 2008 (UTC)
- I think just about the simplest thing you could do that would be immediately clear would be to show two squares side by side with an arrow between them, and the second one showing the result of the transformation. The operation itself is implicit but clear for all the rigid operations considered here (for rotations I would also rotate the labels). Dcoetzee 07:10, 13 May 2008 (UTC)
- Excellent work on the images. To my opinion especially the superimposed animation steps (above left, "group test2") reflect the mappings clearly. The rotated (mirrored) corner labels add to the clarity (but not all are correct yet). −Woodstone (talk) 12:49, 13 May 2008 (UTC)
- I prefer the right version (group test3) for the above reasons. I'd opt for including these (properly sized) in the article. Is it possible to get the white numbers with a tiny little black border, so that they are easier distinguishable from the faded green bullets etc.? Jakob.scholbach (talk) 13:04, 13 May 2008 (UTC)
- Black borders have been added. This is as thin as they go.(TimothyRias (talk) 13:15, 13 May 2008 (UTC))
- Great. Many thanks! I think that's quite an improvement over the current version. Would you add it to the article? Jakob.scholbach (talk) 21:07, 13 May 2008 (UTC)
Done.(TimothyRias (talk) 06:21, 14 May 2008 (UTC))
Examples of groups: Lie groups => group objects
I think we might want consider replacing the Lie groups section with one talking about group objects in general and providing Lie groups as a prime example. We could include a small table of the most well-known examples. (Lie groups, topological groups, Algebraic groups, etc.) Currently, the article might overemphasize Lie groups a little, which could be due to the background bias of the editors. (including myself) (TimothyRias (talk) 08:05, 13 May 2008 (UTC))
- I think Lie groups are is not overemphasized right now. The section does mention group objects. If anything, then algebraic groups etc. are mentioned pretty shortly, but we need to be careful and even restrictive when adding more and more content. None of the examples sections, except the very easy ones, can be more than a glimpse of what is out there. So, I would not change the subsection substantially (except perhaps adding details about applications as requested above in the review). Jakob.scholbach (talk) 13:02, 13 May 2008 (UTC)
I don't think the total length of the article would increase much. Currently the section on Lie groups starts by talking about group objects and then moves to Lie groups. I think it would be more natural to switch the emphasis of the first paragraph completely to group objects and move on to Lie groups. Group objects are important in mathematics and need a more prominent mention here. (TimothyRias (talk) 13:54, 13 May 2008 (UTC))
- Hm, my only concern is that a section having one sentence about group objects and 5 about Lie groups should be titled "Lie groups". But, this is a wiki, so do what you see fit. Jakob.scholbach (talk) 21:01, 13 May 2008 (UTC)
- I think it would be a mistake to overemphasise group objects, and believe me, I absolutely love the ideas like "group object" myself. However, the concept of a group object does not have nearly the same presence and widespread application as the concept of a Lie group, and it is not widespread to refer to a Lie group as a group object in the category of smooth manifolds (an OR issue). Lie groups and algebraic groups have a highly developed representation theory with manifold applications (forgive the pun). Further, in category theory, the concept of a group is not as fundamental as the concept of a monoid. Categories are themselves a generalization of a group, but they only get a few sentences in the "generalizations" section. Group objects in categories, beautiful though they are, need to be developed elsewhere, not here. Geometry guy 19:50, 14 May 2008 (UTC)
Symmetry groups
Partly in response to the concerns about broadness (in particular w.r.t. applications of gps) I added a little section about symmetry groups. Does anybody know of a nice example where a geometrical object was used to prove something about an abstractly defined group? (I know something like growth of the fundamental groups of manifolds with certain curvature, but I'm not sure whether this is used rather the other way round).
- Building (mathematics) is sort of a famous version. Coxeter groups more or less fall in this category. Hyperbolic groups have combintorial group theoretic properties because they act on special manifolds. Hurwitz groups satisfy a presentation because they act on special manifolds. The existence of many of the sporadic simple groups was proven by constructing them as symmetries of finite geometries. JackSchmidt (talk) 21:23, 13 May 2008 (UTC)
- Let me know if this is not clear. Basically using geometric objects to prove things about groups is one of the fundamental methods in group theory. It is hard to think of any major result that does not use this technique. This is sort of the point of the first chapter of Aschbacher's text on group theory, and a point belabored in most geometric group theory texts. The classification of the finite simple groups hinges on the idea that simple groups tend to have a natural geometry associated with them, that geometry is almost always over a field, and that field is almost always the base field of the lie group that your simple group must be equal to. Current research in modular representation theory is bizarrely geometrical (see Benson's texts), and homotopy theory plays a huge rule. A literature search for "quillen complex" or "bouc complex" or "p-local geometry" should give a hint at how big just that tiny subsection of this is. JackSchmidt (talk) 21:34, 13 May 2008 (UTC)
- OK. I added a tiny little piece of the above to the article. Any more complete elaboration of group theory vs. geometry should be deferred to gp. th. Jakob.scholbach (talk) 14:57, 14 May 2008 (UTC)
Applications section
I agree with GG that an applications section would make a nice addition. I think it should go after the examples section and before the generalizations section. Currently the applications are spread out (nicely) in the other sections, so I suggest first we work on Applications of group theory, then we can more easily decide which applications should be mentioned (in any detail) in this article, and whether they should be described more in the individual sections or in the application section (which might get long very quickly).
This will also give this article a chance to rest! With over a hundred edits in the last week (most due to the other leading JS who has tirelessly improved this article to GA), I think we should celebrate and take a break. JackSchmidt (talk) 19:18, 14 May 2008 (UTC)
- Congratulations to all on the GA! I have also commented on my talk page. I'm keeping this on my watchlist for a while longer, but if there's a lull, please ping me when you want to go for FA. Geometry guy 19:38, 14 May 2008 (UTC)
- I think before moving on with Applications of group theory of trying to improve this article to FA, we need to work on Group theory and firmly establish its scope. The current version of that article pretty much overlaps this article, which it shouldn't. (TimothyRias (talk) 07:51, 15 May 2008 (UTC))
- I agree. There is no harm in there being an overlap in the concepts discussed in the two articles, but these concepts need to be approached from a completely different viewpoint in the group theory article: think "how, when, why and where to?" rather than "what?" In other words, the group theory article is not for a reader who wants to know what a group is (this article does that), but for a reader who wants to know why they are important, how they arose, the history of groups, and modern developments. That's quite a challenge. I've watchlisted group theory and will contribute if I can. For an illustration of two articles approaching the same concepts from a different perspective (at a less advanced level), see derivative with differential calculus. Geometry guy 19:09, 15 May 2008 (UTC)
- I have been thinking about apps. I'm a bit hesitating to introduce an application section. It is certainly true that we could write enough for a section here (and a separate article), for example the german article has some material one could easily use. Currently we have coding theory, physics (gauge th., special rel., quantum mechanics), chemistry (crystallography), cryptography, differential equations. I think this is a somewhat representative sample (am I missing something important??). Currently the applications are scattered over the several subsections in the example section. Given a limited total length, the alternative would be writing an application section and moving the stuff to this place. I dislike this because I think the inner coherence of the subjects is better represented if the topics are order according to their mathematical nature, not the fields where they are applied. Comments?
- It is also true that the applications are not exactly "worked". Again, it would be fun and beautiful, to elaborate on the monodromy example, for example. But, helas, I think this would one the one hand be beyond the scope here, and also would increase the article length. So, perhaps, mentioning some interesting cases of applications with very exact pointers to references is also OK. Jakob.scholbach (talk) 17:03, 16 May 2008 (UTC)
references
Why are many of the references referred to in the notes placed in the "further reading" section? I would expect this section to contain only references that were not mentioned in the text. (TimothyRias (talk) 11:52, 16 May 2008 (UTC))
- "Further reading" refers to references which are about more advanced topics. They are usually quoted exactly once in the text. I think it is important to structure the reference section. Jakob.scholbach (talk) 13:38, 16 May 2008 (UTC)
- Is there another way to structure the References section that would achieve the same effect? "Further reading" certainly suggests that the references listed weren't used in the text. silly rabbit (talk) 14:35, 16 May 2008 (UTC)
- OK. Would "Advanced topics" or "Advanced references" be OK? Jakob.scholbach (talk) 15:16, 16 May 2008 (UTC)
- Perhaps you might consider putting two subsections into the References section: the first General references, and the second Specialized references. That seems to better capture the distinction between the two classes of references (rather than easy versus advanced). silly rabbit (talk) 15:42, 16 May 2008 (UTC)
- Good idea. I did so. Jakob.scholbach (talk) 16:22, 16 May 2008 (UTC)