Talk:Covariance and contravariance of vectors/Archive 1

Archive 1

Old comments

Covariant components are mates to contravariant, but covariant transformations are ones that preserve certain invariants, the simplest one perhaps being "dot-products of covariant and contravariant components of the same vector. The distance function is preserved by covariant transformations, but its covariant components are not. The Riemann scalar is preserved by covariant transformations, but its covariant components are not. A merger is out of order.Pdn 04:18, 21 May 2005 (UTC)

I agree that there should be more than one article on this. Perhaps covariant transformation and covariant vector etc. I don't really like the naming now of simply covariant as it's an adjective and seems to preclude any covariant _____ articles. I'm also more than a little frustrated that the mergewith tags have been readded within a day without further discussion. --Laura Scudder | Talk 06:44, 22 May 2005 (UTC)

The conversatation has been moved to Wikipedia_talk:WikiProject_Mathematics. Please go there. linas 07:09, 22 May 2005 (UTC)

Well, long talk threads belong here, not there. I'm going to move this page to covariance and contravariance, since Laura's point about nouns is good (and covariance is taken by statistics right now). Covariant transformation seems to me too confusing a concept to be taken as primary. Charles Matthews 09:31, 27 May 2005 (UTC)

What 'contravariant' means

This section doesn't manage to be very clear. I know about tensors so this section which is only about Euclidean space should be a piece of cake, but it isn't. The only thing that I managed to distill is how contravariant components are formed and the picture makes it clear, although the wording is suboptimal and there is no caption, but the covariant case is neglected. Is there anything else that this section is trying to explain? Something about meaning maybe? Otherwise this section should be scrapped and a brand new section about how to take coordinates written. --MarSch 14:24, 24 Jun 2005 (UTC)

I agree. After half an hour of reading I was not able to determine what 'covariant' or 'contravariant' mean. There is a lot of information which would seem to suplement this knowledge, such as the relationship between the two concepts, etc. But there needs to be a simple intuitive explanation of the basic meaning, because without that all of this information is utterly useless. --Jack Senechal 08:58, 26 December 2005 (UTC)

Example: covariant basis vectors in Euclidean R3

Contravariant vector is not explained and neither is covariant vector and also not what the reciprocal system is. Then the section proceeds to talk of an unqualified vector v. Apparently it is possible to take the dot product of a vector with a contravariant vector and also of a vector and a covariant vector. How is that supposed to work? This section is extremely unclear to me. --MarSch 14:34, 24 Jun 2005 (UTC)

Obtuse

The lay reader needs to walk away from this article with an intuitive understanding of what the covariant and contravariant components of a vector in arbitrary coordinates on an arbitrary manifold are.

Central to this understanding are the notion of a "geometric object", which is a collection of numbers, and a rule, such that if you know the numbers in one coordinate system, you can use the rule to find them in any other, and the notion that a person familiar with vector calculus in three dimensional Euclidian space will seek to make his life as uncomplicated as possible when dealing with curved coordinates in curved spaces.

Eschewing both unit and orthogonal basis vectors, he will seek to pick basis vectors such that the components of a vector have the simplest transformation rule possible, that of a differential, which transforms by multiplication by the matrix of partial derivatives of one set of coordinates with respect to the other. There are two fundamental ways of doing this, depending on whether you differentiate the old coordinates with respect to the new, or the new with respect to the old. These two choices correspond the geometric object being either a covariant or contravariant vector.

An important point here is while the components of the vector change with the choice of basis, the sum of the components times the basis vectors is an invariant independent of coordinate choice, which is the vector as an abstract mathematical object.

Intuitively, in three dimensional curvilinear coordinates, the covariant components of a vector correspond to using basis vectors which are tangents to the coordinate curves, and the contravariant components correspond to using basis vectors which are normals to the coordinate surfaces. If you perturb the coordinate grid lines, the covariant basis vectors will move with the grid lines, and the contravariant basis vectors will move in a contrary manner.

I think I understood that! Could I suggest that you add this in as an introduction at least?62.213.130.74 (talk) 10:12, 10 October 2008 (UTC)

I really don't like the metaphor of drawing the vector on the manifold and projecting it onto the coordinates, because the vector lies in the tangent space to the manifold at a particular point, which is flat, and doesn't have physical extent on the manifold itself, although such handwaving will sometimes seem to give the right answer. Hermitian 04:58, 8 January 2006 (UTC)

I agree. Some new, more effective methods of communicating these important ideas are in order. Corax 22:14, 8 January 2006 (UTC)

Incidentally, note that Corax has never before made any contribution to any article on mathematics (at least under this name). User:Katefan0 and I both expected them of being sockpuppets, as they spend 99% of their time defending NAMBLA. Katefan even went to the length of having their IP addresses checked out, but it seems they're not SPs. However, I expect that Corax's endorsement of Hermitian's comment here may just be a case of the old buddy system, and can be ignored. Camillus (talk) 20:30, 9 January 2006 (UTC)

DON'T FOLLOW THAT NAMBLA LINK WHILE AT WORK! It's not something you want showing on web logs.62.213.130.74 (talk) 10:16, 10 October 2008 (UTC)

What does this have to do with adding clarity to the article on "Covariance and Contravariance?" Are you going to follow me around and troll all my posts because you don't like NAMBLA? (guffaw) Hermitian 21:14, 9 January 2006 (UTC)

Too Technical

I'm by no means new to vectors or tensors, but for the life of me I can't figure out what covariance or contravariance means from this article. I understand that a single (invariant) vector can be written in terms of any number of basis vectors, but I don't see how that relates with co- and contravariance. Could someone explain? —Ben FrantzDale 08:11, 26 March 2006 (UTC)

Let me take another crack at this. I still do not understand what this article is trying to say and it still does not seem to point me in the right direction to find out more. I have two fairly hazy hunches. (1) It seems that this topic deals with the difference between an abstract tensor—an invariant—and a "corporial" tensor in matrix form. It seems that there are two isomorphic numerical representations of a single invariant one being the covariant and the other the contrariant representation. (2) It seems that this topic deals with tensors expressed in terms of parametric coordinates. That is, if I have the vector (1,1) in cartesian space, I could also represent it in terms of another coordinate system with base vectors in the (√½,√½) and (−√½,√½) directions, in which case the same vector would be represented as (√½, 0). It is not clear to be if (1) or (2) or both of the above are right or are even close. Could someone explain? Am I on the right track? —Ben FrantzDale 05:20, 4 April 2006 (UTC)

Aside from the question of whether the article could or should be written more clearly, any discussion of covariance in multiple contexts is bound to be confusing. Physicists will use the term to mean that some mathematical entity is a well-defined geometric object, not an artifact of a particular coordinate choice. Physicists will also use the term in a closely related, but decidedly different, sense in discussing what they call tensors (which mathematicians call tensor fields). This latter use contrasts covariant with contravariant. Then we have mathematicians also talking about tensors, and about tensor fields, perhaps shifting meaning again. And the category theory mathematicians appropriate the same covariant/contravariant terminology for their own, quite different, use.

How do we know whether something is co- or anti-co-? Unfortunately, as with all binary choices, it's a matter of convention. (And often conventions are established too early. Thus electrons, the carriers of electric current, have negative charge; it's too late to call them positive!) Covariance can be extra challenging, because it involves multiple binary choices. Confusion is guaranteed.

In practice we are saved by working in only one context at a time, with only one convention, and with far less confusion. --KSmrq^T 06:56, 4 April 2006 (UTC)

Thanks for the reply. With regard to this article, the definitions I am most interested in understanding is the mathematical one (and perhaps the physics one as well). As the article stands I follow the first paragraph (which says very little) but get stuck at paragraph two:

In very general terms, duality interchanges covariance and contravariance, which is why these concepts occur together. For purposes of practical computation using matrices, the transpose relates two aspects (for example two sets of simultaneous equations). The case of a square matrix for which the transpose is also the inverse matrix, that is, an orthogonal matrix, is one in which covariance and contravariance can typically be treated on the same footing. This is of basic importance in the practical application of tensors.

The duality link isn't much help and the rest of the first sentence seems to say very little.

The second sentence (which isn't quite a sentence), with its talk of matrix transpose, seems to be talking about the rowspace and columnspace of a matrix.

Sentence three isn't clear. For example, what does "typically" mean? What does "the same footing"? mean? I'm inclined to think that this sentence means "when the transpose is the inverse of a matrix, xⁱ=x_i".

Sentence four doesn't add anything.

The third paragraph says a little bit more, but is similarly vague to the new reader, at least. Hopefully this disection will help someone who does know the subject find a place to start reworking the article. —Ben FrantzDale 12:44, 4 April 2006 (UTC)

replies to Ben

1. It seems that this topic deals with the difference between an abstract tensor—an invariant—and a "corporial" tensor in matrix form.

   Yes, the difference between the physicist's convention and the mathematician's convention depends on whether you want to know how components transform under passive transformations or how objects behave under active transformations.

2. It seems that there are two isomorphic numerical representations of a single invariant one being the covariant and the other the contrariant representation.

   There are only isomorphic representations if you have some isomorphism perhaps provided by a nondegenerate bilinear form, usually a metric tensor. The existence of such objects helps to conflate the notions of covariance and contravariance, and so when trying to understand the difference, prefer to consider spaces without such an isomorphism. Insist on strict separation in your mind of covariant and contravariant objects. This applies in either convention.

3. Hopefully this disection will help someone who does know the subject find a place to start reworking the article.

   I'm going to try to see what I can do with this article. In its current state, I have half a mind to just scrap the whole thing and start from scratch. -lethe ^{talk +} 15:55, 4 April 2006 (UTC)

A rewright or major overhaul sounds appropriate. I'd be happy to vet any new material for clarity.

Regarding 1 and looking at active and passive transformation and your section below, it sounds like the physicist's definition goes like this:

If I have a sheet of graph paper with a vector in the (1,0) direction drawn on it and that paper is aligned with a global coordinate system, if I physically rotate the sheet of paper by π/2 right hand up—an active transformation—then the vector will be covariant—it will varry with the transformation and now point in the (0,1) direction.

With the same setup, if I now rotate the global coordinate system by π/2 right hand up, the vector itself is unchanged but its representation in global coordinates is now (0, −1); that is, the vector transformed contravariantly with respect to the passive transformation.

Is that about right? —Ben FrantzDale 20:32, 4 April 2006 (UTC)

I think it's difficult to see the full picture if you only talk about components. Let's look at the components of the vector as well as the basis. Start with a basis e₁ and e₂, and components 1 and 0. So your vector is v = 1e₁+0e₂. Imagine those basis vectors attached to your sheet of paper. Rotate the sheet of paper, and e₁, e₂ and v all rotate as well. The new rotated vector is now v'= 1e'₁+0e'₂. Notice that the components didn't change: the vector is still (1,0). The components of the vector are just numbers, scalars, they do not transform. Vectors transform (covariantly), scalars do not. New basis vectors, same components, new vector.

Now imagine rotating your global coordinates, and re-writing the basis vectors in terms of the new coordinates. To get the same physical vector in terms of the new basis vectors, we change the components as well; the vector is v=0e'₁–1e'₂. The physical vector stays the same, but the components and the basis vectors transform (the vector covariantly, the components contravariantly). New components, new basis vectors, same resulting linear combination. -lethe ^{talk +} 21:16, 4 April 2006 (UTC)

I agree completely. Well put. I think we are making progress! —Ben FrantzDale 21:55, 4 April 2006 (UTC)

My attempt to explain

Covariance and contravariance is at its heart quite simple.

Covariant things in a space transform forward along transformations of the space, contravariant things transform backwards along tranformations of the space.

If you always work in a coordinate-independent way, things stay cleaner, and the situation is pretty simple. Vectors are covariant, functions and differential forms are contravariant (in apparent contradiction of the physicists' convention).

When you introduce local coordinates, you now have two kinds of transformations to consider: active transformations, which can move vectors and tensors around, and passive transformations, which change the basis, but leave other tensors fixed. (Active transformations are diffeomorphisms of manifolds, while passive transformations are transition functions on manifolds).

Under an active transformation, basis vectors, being vectors, are covariant, while their components, being scalars, do not change. Functions do not change, and the basis one forms change contravariantly while components do not change. The total object changes. This is the same statement as above, but viewed in local coordinates.

Under a passive transformation, we need the product of the components with the basis to remain unchanged. The basis vectors, being vectors, still transform covariantly (covariantly is the only possibly way to change any vector under a smooth map unless it's invertible), so in order to keep the total object invariant, the components have to change contravariantly. Similarly, the basis of one forms change contravariantly (the only way they can) and to keep the total object invariant, the components have to change covariantly.

Thus the physicist, who thinks of the object solely in terms of its component and its behaviour under passive transformations, calls the vector contravariant and the one-form covariant, while the mathematician who thinks of the total object and how it behaves under active transformations (morphisms in the category of manifolds) calls the vector covariant and the one-form contravariant. -lethe ^{talk +} 15:36, 4 April 2006 (UTC)

That's a big help; the article is starting to make more sense. Is this related to the notion that the result of a cross product is a pseudovector or that a surface normal doesn't transform nicely under non-orthogonal transformations? —Ben FrantzDale 20:52, 4 April 2006 (UTC)

Well... if you'd like to think of it in terms of representation theory, for every representation of GL(n), there is a bundle whose vectors transform according to that rep. The tangent vectors transform according to the fundamental representation, covectors transform according to the dual representation, pseudovectors transform according to GL+(n) (the connected component of GL(n)), and if there is a metric tensor, all these groups can be reduced to the O(n) subgroup. To answer your question, contravariance versus covariance has some bearing on what representation you use, and so does pseudovectorness and orthogonality, but the notions are still independent. You can be a pseudovector or a pseudocovector, or a vector or covector, each is a different rep of GL(n). -lethe ^{talk +} 21:27, 4 April 2006 (UTC)

Wow. That was totally over my head. I wouldn't bother trying to explain that to me in any more depth right now. —Ben FrantzDale 21:55, 4 April 2006 (UTC)

Well, I was really stretching to figure out a way to relate pseudoness to covariance. A mention of represetnation theory might deserve only a footnote. -lethe ^{talk +} 22:06, 4 April 2006 (UTC)

It is possible to unify normals and vectors and dualities by embedding everything in Clifford algebra, but that's probably not the best step for you at this point in your learning. Let's try something different. A surface normal is part of a plane equation, typically written in matrix notation (using homogeneous coordinates) as 0 = G p. The G part is a "row vector", which is another way of saying a 1-form; the p part is a column vector, which is another way of saying just an ordinary vector. By a 1-form we mean a linear function from a vector space to real (or complex) numbers, the latter also consider a (trivial) vector space. The homogeneous coordinates are a nuisance required to handle an affine space with vector space tools. If we fix an origin and only consider planes through it, we can dispense with the extra component of homogeneous coordinates. Then G is precisely a normal vector.

A differential manifold, considered intrinsically, does not have a normal. "Normal" is a concept that only makes sense for a manifold embedded in an ambient space, like a spherical surface (a 2-manifold) embedded in 3D Euclidean space. Most of differential geometry as applied to general relativity has to work intrinsically. Most of our early intuition for it comes from the embedded examples.

So let's think about a simple smooth curving surface M embedded in 3D. Concentrate attention on a single point p∈M. Extrinsically, we have a unique plane tangent to the surface at that point. Intrinsically, we have a tangent space. This is a clever construct, but takes some practice to absorb. Consider all the smooth curves, C(t): R→M, passing through our point p. Switch attention to all the possible derivatives of those curves, dC/dt, at p. (To make it simple, parameterize the curves so that always C(0) = p.) This collection of derivatives becomes the tangent vector space, T_pM. For intuition, it helps to thing of the (extrinsic) tangent plane as a stand-in for the (intrinsic) tangent vector space, taking p as the origin.

When mathematicians speak of a tensor, we mean a function that takes some number of vectors and produces a real number, and that is separately linear in each vector argument. For example, the dot product of vectors u and v yields a real number that depends linearly on both u and v, so "dot product" is a "rank 2 tensor". Here "rank" refers to the number of vector arguments. More precisely, we have just defined a covariant tensor.

Linear forms over a vector space, such as the tangent space, comprise a vector space in their own right — a dual space. We can just as easily speak of multilinear functions, tensors, that take dual vectors (forms) as arguments. These are contravariant tensors. We can also have mixed tensors.

When physicists speak of a tensor, the meaning shifts. No longer are we talking about objects defined on a single vector space, T_pM, and its dual. Now we are talking about an object defined across all the tangent spaces, TM (and their duals). Mathematicians prefer to call this a tensor field, a (continuous) mapping from points p∈M to (mathematicians') tensors. We do insist on continuity, thus the rank and covariance/contravariance are the same at every point.

Because physics is based on experiment, the question naturally arises if some experimentally or theoretically discovered mapping from points to functions, defined in terms of coordinates, has intrinsic meaning. Does it fit the mathematicians' definition of a tensor field? If it does, old physics terminology proclaims this thing "covariant", a third meaning. Sigh.

Does this help? --KSmrq^T 00:21, 5 April 2006 (UTC)

more technical

I've started a rewrite of this article, wherein I hope to make the difference between the different conventions for co- and contravariant completely transparent. Unfortunately, as I write it, I find I'm writing an article that is far more technical than the existing article, rather than one that is less technical. It is important that we have an article which is mostly comprehensible to, say, someone encountering special relativity for the first time. This person may not have the slightest idea what a manifold or a topological space is. So this is actually a hard article to write. -lethe ^{talk +} 16:39, 4 April 2006 (UTC)

Sounds good. Where's the draft? I'd say write what comes naturally and then we can work on translating it to something more reasonable for beginners. The more I look at the current version of the article the more I think the problem isn't that it's too technical but that it's just incoherent. I might have a chance of understanding a fully-technical article by following enough links. —Ben FrantzDale 20:36, 4 April 2006 (UTC)

The draft is at User:Lethe/covariance, but be warned, I'm not sure if it's a suitable direction for an article on this subject, and even if it is, it's still very much a work in progress. -lethe ^{talk +} 21:19, 4 April 2006 (UTC)

It looks like a good start. I'll watch it. —Ben FrantzDale 21:55, 4 April 2006 (UTC)

What this article seriously needs is a split, either internally or externally. By simultaneously trying to discuss all the variations, it only succeeds in causing confusion. We need clear separation between physics, tensor mathematics, category theory, geometric objects, and coordinate systems. Instead we have a witches' brew, with a little eye of newt here and wool of bat there. Yuck. --KSmrq^T 23:08, 4 April 2006 (UTC)

I would really like it if this could all be covered clearly in one article. Treating covariance in physics and mathematics as separate and different notions I think makes the concepts harder to understand. I'm not sure it can be done well, but I'm going to try. Give me some time to see what I can come up, and then let's decide whether we need to split. -lethe ^{talk +} 23:45, 4 April 2006 (UTC)

As a relative layperson (someone who shouldn't encounter covariance/contravariance for about 8 months on eir mathematics course) I've encountered both manifolds and topological spaces. Is it really likely that such a technically advanced notation will attract the interest of laypeople? 12:30, 16 May 2007 (UTC)

New Figure and Descriptions Added

Dear All, it seems apparent that the meanings of contravariance and covariance were not clear to most readers. Therefore I've added another figure showing how the component-wise basis vector terms are oriented in a 2D curvilinear and non-orthogonal grid to represent some generic vector. I am also going to add some bits on the transformation properties of the basis vectors. It may be a little rough at first, so I definitely invite anyone to clean up the notation and presentation...

...OK, I've put a ton of new stuff in there, but it is still not entirely complete. —Preceding unsigned comment added by Hernlund (talk • contribs)

Please sign your messages with "~~~~". Also please put new messages at the BOTTOM of the talk page, not at the top, in accordance with accepted practice. Thanks for your contribution to the article. JRSpriggs 06:59, 10 November 2006 (UTC)

Illustration of the contravariant and covariant representation of vectors in a 2D curvilinear, non-orthogonal grid

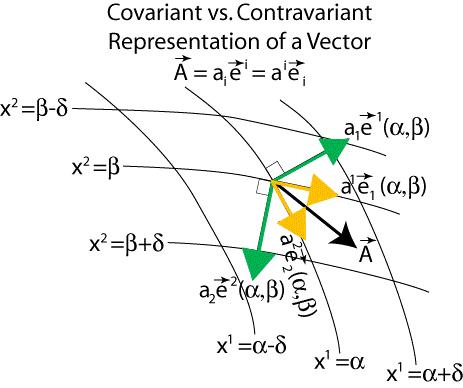
With regard to the figure, why is $\mathbf {e} _{2}$ tangent to the line labeled $x^{1}={\alpha }$? Shouldn't it be tangent to the line labeled $x^{2}={\beta }$? I have a similar comment about $\mathbf {e} _{1}$; I think it should be tangent to $x^{1}={\alpha }$ instead of $x^{2}={\beta }$. ChrisChiasson 12:33, 7 January 2007 (UTC)

Those vectors point in the direction that the corresponding variable changes. The lines you are referring to are lines along which the variable does NOT change. So e₁ points in a direction in which x₁ changes and all other variables (including x₂) do not change. JRSpriggs 13:17, 7 January 2007 (UTC)

So the contravariant unit vectors are actually orthogonal to all other coordinate axes (besides their own)? ChrisChiasson 01:42, 9 January 2007 (UTC)

Orthogonality does not enter into contravariant vectors. Consider the fact that the x-axis in the x-y-plane is given by the equation y=0. Similarly the y-axis is x=0. The contravariant e^x vector at a point is directed along the constant-y line through the point. Whereas, the covariant e_x vector is perpendicular to the constant-x line through the point. In this plane they appear to be the same vector. JRSpriggs 07:57, 9 January 2007 (UTC)

"Whereas, the covariant e_x vector is perpendicular to the constant-x line through the point." - I'm lost :-[ Does this mean the picture should have e₁ perpendicular to x¹? ChrisChiasson 23:20, 9 January 2007 (UTC)

Sorry, I was the one who was confused. I am not used to thinking about the basis vectors. Frankly, I do not find them helpful. So I was reversing contravariant and covariant in my mind and in my last message. The picture is correct. The covariant e_x vector at a point is directed along the constant-y line through the point. Whereas, the contravariant e^x vector is perpendicular to the constant-x line through the point.
So the answer to your question "So the contravariant unit vectors are actually orthogonal to all other coordinate axes (besides their own)?" is Yes.
In most of the books I have read on this subject and in my own thinking, the sequence of components (coefficients) $\langle {a^{1},a^{2},...,a^{n}}\rangle$ IS a contravariant vector. And the sequence of components $\langle {b_{1},b_{2},...,b_{n}}\rangle$ IS a covariant vector. The basis vectors vary the opposite way from their associated components, i.e. contravariant components go with covariant basis vectors and vice-versa. JRSpriggs 10:26, 10 January 2007 (UTC)

It would be informative to see unit vector field plots of e₁, e₂, e¹, and e², along with streamlines (defining coordinate axes?) (created by solving the differential equations defining the vector field and the initial conditions from selecting an initial point) and constant coordinate lines (e.g. x² = 15). I would create them, but I think I would do it incorrectly because I don't really understand general curvilinear coordinates. ChrisChiasson 18:50, 12 January 2007 (UTC)

The way that I think of them is (as I wrote in the article some time back)

A contravariant vector is one which transforms like ${\frac {dx^{\mu }}{d\tau }}$, where $x^{\mu }\!$ are the coordinates of a particle at its proper time $\tau \!$. A covariant vector is one which transforms like ${\frac {\partial \phi }{\partial x^{\mu }}}$, where $\phi \!$ is a scalar field.

That is a contravariant vector is like a little arrow, e.g. velocity. A covariant vector is like a gradient which could be better visualized as a set of level lines rather than as an arrow. The arrows shown in these diagrams for the covariant vectors are just the normal vectors which are actually contravariant vectors perpendicular to the level lines. What is being hidden here is the metric tensor which is being used implicitly to convert between covariant and contravariant. JRSpriggs 08:21, 13 January 2007 (UTC)

Understanding

I think I finally get it. Too many years thinking in an orthonormal basis rotted my mind; this isn't too complicated. Here's the beginning of the explanation I needed. If it's accurate, I'll incorporate it (with diagrams) into the article.

When vectors are written in terms of an orthonormal basis, the covariant and contravariant basis vectors align, so the distinction between the two is unnecessary. In an orthonormal basis, the components of a vector are determined by dotting the vector with each basis vector, so a vector, x, that points up and to the right with a length of ${\sqrt {2}}$ is the vector (1,1) in the usual basis. We will first consider basis vectors of different lengths, then consider non-orthogonal basis vectors.

Consider two basis vectors, e₁ points right and is two units long and e₂ is one unit long and points up [image]. By inspection, x written in this coordinate system is (1/2,1). This was determined by projecting x onto these two directions, but also scaling so that $\mathbf {x} =x^{i}\mathbf {e} _{i}$. That is, for orthogonal basis vectors that are not necessarily unit length,

$x^{i}=\mathbf {x} \cdot \mathbf {e} _{i}/|\mathbf {e} _{i}|^{2}=\mathbf {x} \cdot {\frac {\operatorname {normalized} (\mathbf {e} _{i})}{|\mathbf {e} _{i}|}}=\mathbf {x} \cdot \mathbf {e} ^{i}.$

This vector, $\mathbf {e} ^{i}$, is the contravariant basis vector.

Now consider the case of a skiewed coordinate system such that $\mathbf {e} _{1}$ is a unit vector to the right but $\mathbf {e} _{2}=\mathbf {x}$. Obviously we expect x represented in this coordinate system to have coordinates (0,1). Again, projecting onto each vector does not give the coordinates of x. The correct vectors to project onto—the correct linear functionals—are the contravariant basis vectors [image].

That's a start. Feel free to rephrase the above. —Ben FrantzDale 18:03, 10 May 2007 (UTC)

This makes a _lot_ more sense now. Huzzah for concrete examples! —Preceding unsigned comment added by 98.203.237.75 (talk) 09:28, 7 January 2008 (UTC)

I think the image is useful but could be improved if the contravariant and covariant basis vecotors were in different colours. —Preceding unsigned comment added by 137.205.125.78 (talk) 12:02, 23 April 2008 (UTC)

Merge

I re-added the proposal to merge with Covariant transformation. This page and that may both deserve to exist, but at the moment, the two seem redundant. If they aren't merged completely, they should be refactored so that one page (this one?) is an introduction and the other goes into detail. —Ben FrantzDale 13:26, 11 May 2007 (UTC)

progress?

I was just checking back on this page, to which I had added the transformation laws and the figure on a non-orthogonal grid some time ago. I was curious whether people were understanding the difference between covariant and contravariant better after this addition, and it seems there might still be some confusion, though matters may have improved a bit after that. Another way to look at this is constrasting how the differentials vs. the gradient vectors of a coordinate system transform...one gets the same results as the contravariant and covariant laws in these scenarios as well. I'd like to know if there is anything else I can contribute...drop a note here, and I'll read it later on and work on it over time, as I'm a rather busy fellow. Cheers! Hernlund (talk) 03:33, 22 November 2007 (UTC)

To be honest, I still don't really understand. On the other hand, I don't use tensors often. However, I have never had any formal training with them. Please don't feel obligated to improve the article; only do it if you want to - and thanks! ChrisChiasson (talk) 14:41, 22 November 2007 (UTC)

covectors: above or below?

It seems that amateurs are trying to bring more confusion between covariant and contravariant issues but just as a mnemonic device remember that coordinated functions are indexed above $x^{\mu }$ and then differential forms also $dx^{\mu }$ (reason: coordinated functions are linear and also its differentials are indexed above), and as everybody knows in electromagnetism: $dA=F$ which in components means

$F_{\alpha \beta }=A_{\alpha ,\beta }-A_{\beta ,\alpha }\,$

for the covector potential $A=A_{\mu }dx^{\mu }\,$ and the bivector force $F=F_{\mu \nu }dx^{\mu }\wedge dx^{\nu }$, in an holonomic frame. Conclusion, this article sucks!... 'cuz (further) it brings more confusion to the non-experts, besides there, in Eric Weinstein stuff, it is wrong... it is better to check against Misner-Thorne-Wheeler's Gravitation--kiddo (talk) 04:28, 10 March 2008 (UTC)

the title is misleading in the first place

Dear Wikipeditors,

First of all the title is misleading since it concerns not only "vectors" but also "covectors", both of which are a special case of tensors, namely 1-tensors. This should also be made clear to the reader in the introduction of the article. The first question is whether or not there should be a separate article concerning this special case. In my opinion the whole matter should be dealt within the article about tensor. The reason is that co- and contravariance aren't really concepts themselves. However "covariant 1-tensors" and "contravariant 1-tensors" are. I think this is one of the reasons why students in general are confused about these things. If everything is stated in a precise and unambiguous manner it shouldnt really be confusing: A contravariant 1-tensor (or (1,0) tensor) corresponds to a vector. For physicists such a tensor x is a set of tuples a=(a_1,...,a_n) for EACH basis. However, one is not allowed to chose these tuples independently. The extra condition is that a_1 = M a_2 if a_1 and a_2 are the tuples of x with respect to two given bases and M is the change of coordinates matrix. Hence this notion is really the same as the notion of vector, only that we specify the coordinates with respect to all bases simultaneously. A covaraint 1-tensor is (or (0,1) tensor) has a different definition and corresponds to a covector (i.e. a linear transformation V \to k). Similarly this is a set of coordinates for each basis. The condition in this case will instead be a_1 = (M^T)^{-1} a_2. The reason one uses this definition is that the tuples should correspond to the coordinates of covector with respect to all possible choices of basis. (See below).

There is also a "subarticle" Classical_treatment_of_tensors in the article tensor which should be expanded. There it would be a good idea to start of with 1-tensors before proceeding to the general case. As I said, I think the whole matter must be discussed within the setting of tensors.

Furthermore, I think that the notion "components" of vectors is also presented in a confusing manner, and should be properly defined. The argument for why a covector transforms by the inverse transpose is completely adequate, and possibly incorrect. A proper explation only takes a few lines:

If two bases B_1 and B_2 are given and [x]_1 and [x]_2 are the corresponding coordinates of x, let f be covector. Denote the coordinates of f with respect to the two bases similarily. We then have by definition (1) [f]_1^T [x]_1 = [f]_2^T [x]_2 and (2) [x]_2 = M[x]_1 for all x. We now want to compute the matrix that transforms [f]_1 into [f]_2. Subsituting (2) into (1) yields [f]_1^T [x]_1 = [f]_2^T M [x]_1, which implies [f]_1^T = [f]_2^T M. This gives that indeed [f]_2 = (M^T)^{-1}[f]_1.

Yours sincerely, Zariski —Preceding unsigned comment added by Zariski (talk • contribs) 19:03, 19 March 2008 (UTC)

Section: Rules of covariant and contravariant transformation

there seems to be a contradiction between the first two paragraphs. the first paragraph states that "vectors are covariant ... but the components of vectors are contravariant" but then the second paragraph introduces both the "covariant components" and the "contravariant components" of the vector. this needs clarification in my view. —Preceding unsigned comment added by 77.125.152.181 (talk) 05:00, 26 July 2008 (UTC)

Remark on reference frames, etc

Although the assertion covariance and contravariance refer to how coordinates change under a change of basis seems about right, the next few sentences try to say roughly that "vectors in V have contravariant components" and "vectors in V* have covariant components". This is almost completely unintelligible, since the space which contains the "basis" has not been specified. Moreover, the article seems to use this as a definition of co(ntra)variance, which is putting the cart before the horse: the idea behind covariance and contravariance is that one can describe what a vector "looks like" without making any firm commitments about where it "lives" (i.e., without referring to the space V).

I would like to move back to a more physics-oriented language in this article. Instead of bases, let's consider using reference frames instead: these are bases which play a special role apropos of co(ntra)variance. A reference frame F is a basis of an auxiliary linear space V: that is F is an isomorphism F:Rⁿ→V. (The space V plays very little role in what follows.) Two reference frames F and F′ are related by a unique matrix: F′=FM.

A contravariant vector is an Rⁿ-valued function x on the collection of all frames that associates to each frame F an element x(F) of Rⁿ satisfying

$x(FM)=M^{-1}x(F).$

A covariant vector is a function x(F) such that

$x(FM)=M^{T}x(F).$

For example, let v∈V and define x(F) = F^-1v to be the components of v in the basis F of V, then x(F) defines a contravariant vector. If α∈V^* is a dual vector, and x(F) = F^*α are the components of α in the dual basis (here F^*:V^*→Rⁿ is the transpose of F), then x(F) defines a covariant vector.

I'm not sure how to incorporate this into the article in an intelligible way, but the "Definition" section should be overhauled at least to give a definition which conforms to this more standard usage. siℓℓy rabbit (talk) 13:47, 13 October 2008 (UTC)

I suspect it might be best to junk this whole article and start again based on covariant transformation, which is far far clearer.

What you are suggesting may be correct mathematically, but I suspect physicists (at least on being introduced to the concept) are much happier with the more concrete "transforms like the basis vectors" (covariant) and "transforms like the coordinates" (contravariant), leaving the vectors as columns in both cases.

Thus a new basis vector gets defined by ${\hat {x}}^{\prime }=\alpha {\hat {x}}+\beta {\hat {y}}+\gamma {\hat {z}}$, etc, leading to the matrix equation

${\begin{pmatrix}{\hat {x}}'&{\hat {y}}'&{\hat {z}}'\end{pmatrix}}={\begin{pmatrix}{\hat {x}}&{\hat {y}}&{\hat {z}}\end{pmatrix}}A,$

where ${\hat {x}},{\hat {y}},{\hat {z}}$ are all column vectors; while vectors of coordinates change in the corresponding (contravariant) way

${\begin{pmatrix}v_{x'}\\v_{y'}\\v_{z'}\end{pmatrix}}=A^{-1}{\begin{pmatrix}v_{x}\\v_{y}\\v_{z}\end{pmatrix}}$

Certainly, one can then introduce 1-forms and covectors as functions mapping Rⁿ -> R¹; but these are much more abstract, less familiar things. Better, I suspect for most physicists, to introduce the concept with the more familiar and concrete column vectors first. Jheald (talk) 14:29, 13 October 2008 (UTC)

Standardize with "coordinate vector"

I just made some edits to the exposition of the definition to emphasize the duality. With regards to the terminology of "components" vs. "coordinates", coordinates, while used frequently in this article to refer to different things, are (as far as I know) the correct terminology for what is referred to in this article as "components" of vectors. I am wondering if the article should be made to follow the "coordinate vector" notation. Romistrub (talk) 03:52, 26 July 2009 (UTC)

The notation in coordinate vector is not really suitable for doing index calculations. Thus, in the notation here, we can write vⁱ[f] for the ith component of v in the basis, there is no way to represent this same information in the notation at the coordinate vector article. Most notation in tensor analysis does not emphasize the basis at all, which is an enormous potential source of confusion. The notation here was adopted from R.O. Wells's Differential analysis on complex manifolds, and is consistent with, for instance, the metric tensor article. Sławomir Biały (talk) 14:17, 31 July 2009 (UTC)

Covariance, contravariance and Invariance

Excuse me if I remember the theoretical physics, but in entire article the notion of "invariant" could do clarity on the need of introducing the dual parts of covariants and contravariants (it would be possible to exchange between them, without a modification of the invariant!) Imbalzanog (talk) 20:32, 30 August 2009 (UTC)

I, too, have a concern about the clarity of the difference between covariant and contravariant transformations. The discussion of rotations should come before covariance and contravariance. Covariance and contravariance describes how a tensor transforms with respect to dilation, NOT a rotation or other lorentz transformation. For example, for a covariant vector expressed in coordinates $\xi ^{\mu }$ or $\xi '^{\mu }$, $da_{i}={\frac {\partial \xi '^{i}}{\partial \xi ^{k}}}da'_{k}$, while for a contravariant vector, $da^{i}={\frac {\partial \xi ^{i}}{\partial \xi '^{k}}}da'^{k}$. For a rotation or other lorentz transformation, ${\frac {\partial \xi '^{i}}{\partial \xi ^{k}}}={\frac {\partial \xi ^{k}}{\partial \xi '^{i}}}$, because the projection of one unit vector on another is reflexive. As another example, a lorentz transformation is often represented by $\gamma _{\nu }^{\mu }$, which shows scaling invariance. The implication that a rotation of a covariant vector is the reverse of a contravariant vector is at best misleading. I will wait at least a day for comments before making a change to this article. Rudminjd (talk) 16:46, 6 October 2009 (UTC)

Wrong!

This article is almost completely wrong and muddled. Especially from a physical point of view (spacetime geometry), vectors are a false abstraction, a compound category of objects which do not belong together. 1-forms, 2-forms, 3-forms, genuine vectors and bivectors have been taught using a metaphor taken literally of the arrow sort of vectors. But they are all their own kind of mathematical object.

Genuine vectors are inherently contravariant, these are the objects that you can visualize as an arrow located at a particular place. When you also correctly visualize co-ordinates as dilating and contracting, moving, rotating and skewing, you can see that the arrow representing the genuine vector stays put - does not change location, direction or length. The word contravariant comes from an obsolete co-ordinate-based understanding of vectors. When the basis vector for a co-ordinate grows, the numerical value for the corresponding component of the original vector shrinks. A vector is measured in units of length, or in units transformable to length by use of Planck relativity.

A 1-form is actually what is meant by the term, covariant vector. When the basis vector for a co-ordinate grows, the numerical value for the corresponding component of the 1-form also grows. This is what is meant by covariant in this context. A 1-form is measured in units of length to the minus one power. It is visualized as an array of partitions, with positive and negative orientation indicated perpendicular to the surfaces. Closer spacing of the partitions gives a higher numerical value for the co-ordinate-based components.

 —Preceding unsigned comment added by 99.18.99.23 (talk) 18:12, 27 October 2009 (UTC) 

I agree with all of the above, yet also agree with the article. Where is the inconsistency that you are worried about? 71.182.247.220 (talk) 20:45, 27 October 2009 (UTC)

A phony vector does not remain unchanged in orientation and size when the co-ordinate system skews or dilates. It is a mark of the correct geometric representation of an object that it is not modified by mischief done to the co-ordinate system. —Preceding unsigned comment added by 99.18.99.23 (talk) 21:23, 27 October 2009 (UTC)

Let's be specific please. What line of text do you object to? 71.182.247.220 (talk) 22:03, 27 October 2009 (UTC)

In the last part of the Introduction section:

- If space itself does contort as mentioned, not merely the co-ordinate system, then the vector should be understood as contorting with the space, unless it is a material object.

- There was once or again language there about the electric field being a contravariant vector. But best practice in general relativity is to make it part of a 2-form - neglecting higher dimensions.

- The length, width and height of the box mentioned in the introduction are indeed understandable as contravariant since a dilation of co-ordinates will reduce their numerical value.

- A covariant vector, actually a 1-form, is not different in behavior from contravariant when the co-ordinate system is rotated.

In the first part of the "Covariant and contravariant components of a vector" section:

It should be remarked that the "dot product" operation simply hides the distinction between covariant and contravariant vectors. There is a hidden use of the metric tensor that converts one of the input vectors to a covariant 1-form.

The diagram represents the covariant vectors as arrows, so long as they are in a dual (inverse) space. But ordinary space, where physics is done, does not allow for this representation. Engineers and physicists need to use the diagrams proper to a 1-form - oriented arrays of surfaces. This is to avoid the trap of misrepresentation that will be set off by any dilation of the co-ordinate system. —Preceding unsigned comment added by 99.18.99.23 (talk) 21:39, 28 October 2009 (UTC)

I'll respond to a few of your objections. Your first point is a good one. The text should read something like "if the coordinates of space are stretched, rotated, or twisted, then the components of the velocity transform in the same way." Secondly, this is not the place to engage in a discussion of whether the electric field is "really" a 2-form or is a vector field. Our article electric field states, as it should, that the electric field is a vector field, and there seems to be no risk of confusion in presenting here the electric field as a vector. I disagree strongly with your third point: the dimensions of a box are each scalars, meaning that they are invariant under all coordinate changes. So this is definitely not a contravariant vector. I've added a sentence to the end of the introductory section to address your fourth point: that a vector and covector are indistinguishable wrt rotations. This is also a point made in the previous section. Finally, I'm not claiming that the section on covariant and contravariant components is perfect. But I also find the objection to it somewhat incoherent. Are you sure that you have properly understood the section? 71.182.241.79 (talk) 11:07, 29 October 2009 (UTC)

The presentation of the electric field as a vector is a conventional teaching which is outright contrary to good physics, namely the principle of general covariance. The convention leads to contradiction that is discoverable by a simple practice of diagramming. So confusion does indeed follow from the convention.

It is as germane to counter this kind of bad practice in a mathematical article as in an article on physics, especially since the bad practice is endemic to academic physics.

The dimension of a box has units of length. It is simply bad physics to think of this as a scalar. Once again general covariance applies, and contradictions can be derived from a diagram.

99.18.99.23 (talk) 05:31, 1 November 2009 (UTC)

Again, units of length do not necessarily mean that something is contravariant. The arclength of a piece of string has units of length, but is a scalar. (Or, if you like relativity theory, the proper time along a worldline also has units of relativistic length.) Same thing with the length, height, and width of a box. 173.75.158.194 (talk) 19:52, 4 November 2009 (UTC)

An entity measured in inches or centimeters, for instance, is indeed contravariant, not a scalar, because a shift in size of the basis yields a contrary change in the magnitudes derived from a reading of the object's coordinates. Arc lengths, proper times, and box sizes are all contravariant.

But a wave number is covariant, measured in radians per meter.

Keeping this discipline in mind is marvelously conducive to the understanding of physics.

99.18.99.23 (talk) 02:22, 5 November 2009 (UTC)

I'm sorry, but this is simply wrong. The statement "I have just travelled one light-second along my worldline" is totally independent of the coordinate system used to represent space time. Even if my coordinates are in furlongs per full moon, the units of light-seconds only come in through the metric tensor. And unless one adopts this convention, then the metric tensor itself would be dimensionless (by your argument neither covariant nor contravariant), which is clearly an absurd state of affairs. 173.75.158.194 (talk) 13:12, 5 November 2009 (UTC)

Matrix applied to vector?

The first section after the table of contents includes this sentence:

Mathematically, if the coordinate system undergoes a transformation described by an invertible matrix M, so that a coordinate vector x is transformed to x′ = Mx, then a contravariant vector v must be similarly transformed via v′ = Mv.

I'm confused by two things:

1. To me, this seems ambiguous since this article needs to be very clear and precise about the distinction between a vector and its coordinates with respect to a particular basis. If M is a matrix but x is an order-1 tensor, then M x doesn't make sense because that's multiplying a matrix by a tensor. It seems that M really should be an invertible linear endomorphism on the space of x.
2. If M maps x to x′ and x is a basis vector (I assume that's the meaning of "coordinate vector"), then it looks like v is being transformed the same way, which would be wrong. If M is a passive transformation, just changing the basis from x to x′, then the order-1 tensor v should be left untransformed while its components get represented in the primed system.

For 1, I think it's that

$\mathbf {x} '=M\mathbf {x}$

and since it's saying that the xes are coordinate vectors, that really means there are d of them indexed by lower indices:

$\mathbf {x} '_{i}=M\mathbf {x} _{i}$.

and so we can represent M as a matrix by using another basis, e

$\mathbf {x} '=\mathbf {e} _{i}x'^{i}=\mathbf {e} _{i}M_{j}^{i}\mathbf {e} ^{j}\mathbf {x}$ (I hope I have those raised and lowered indices right.)

or just

$x'_{i}=M_{i}^{j}x_{j}$.

For 2, if v really is contravariant, won't its components transform as

$v'^{i}={\tilde {M}}_{j}^{i}v^{j}$?

—Ben FrantzDale (talk) 14:38, 4 December 2009 (UTC)

The intended meaning is that if the coordinates themselves transform by a matrix, then the components of a contravariant vector transforms by the same matrix. Thus if $x^{i}\mapsto M_{j}^{i}x^{j}$ then $v^{i}\mapsto M_{j}^{i}v^{j}$. I hope that clarifies the matter. Sławomir Biały (talk) 14:41, 4 December 2009 (UTC)

I've got my head hurting :-)

If I understand you, you are saying that

$\mathbf {x} =\mathbf {e} _{i}x^{i}$

and so if you want to have a basis of xes, you would write them, indexed by j as

$\mathbf {x} _{j}=(\mathbf {x} )_{j}=(\mathbf {e} _{i}x^{i})_{j}$

which we can turn back into indices with

$\mathbf {e} ^{k}\mathbf {x} _{j}=\mathbf {e} ^{k}\mathbf {e} _{i}(x^{i})_{j}=\delta _{i}^{k}(x^{i})_{j}=x_{j}^{k}$.

So if we apply M to the indices of the basis, we get

$x'{}_{k}^{i}=M_{j}^{i}x_{k}^{j}$

or equivalently

$\mathbf {x} '{}_{k}=\mathbf {e} _{i}x'{}_{k}^{i}=\mathbf {e} _{i}M_{j}^{i}x_{k}^{j}$$=\mathbf {e} _{i}M_{j}^{i}\mathbf {e} ^{j}\mathbf {x} _{k}$.

where this is all an active transformation of the contravariant vectors x₁, x₂, etc.

If that's right, I think you are saying the components of v expressed in terms of the x_i basis change (so as not to change the vector v itself) as follows when switching to the $\mathbf {x} '{}_{i}$ basis:

$\mathbf {v} =\mathbf {x} _{i}v^{i}=\mathbf {x} '_{j}M_{i}^{j}v^{i}$

and so

$v'{}^{i}=M_{j}^{i}v^{j}$.

I'll check that... I think I am mostly confused because I didn't expect this explanation in the text to be explaining this fact; it's sort of higher-order than the fact that contravariant components vary contravaraintly, and it is easy to get confused and think it is saying the reverse.

Along those lines, is $\mathbf {e} _{i}$ a "covariant basis" or a "contravariant basis"? I could see either word making sense as its the basis used for contravariant vectors but it has a lower index. (I think conceptually it is a one-form of vectors.) Thanks. —Ben FrantzDale (talk) 20:54, 4 December 2009 (UTC)

I'm not sure how you got all of that out of my reply. The sentence in question is saying something much more naive. Giving coordinates on space associates to each point of space a list of numbers. If you change that list of numbers by an invertible matrix, then the components of a contravariant vector change in the same way as that list of numbers. (Coordinates themselves are contravariant with respect to changes in the reference axes.)

To answer the second part of your reply, the basis e_i is clearly covariant with respect to changes in itself: this is essentially a tautology. However, one must not then get the idea that e_i are then individually "covariant vectors": they are (if there is such a thing) "contravariant vectors" or, taken together, a basis of the space of "contravariant vectors". This is part of the reason that I tend to think it is best to avoid dubbing a vector covariant or contravariant. Rather those terms ought to be reserved for the components in a basis. Otherwise genuine confusion of the kind you indicate can result. Sławomir Biały (talk) 23:53, 4 December 2009 (UTC)

Correction

The Introduction says that the electric field is an example of a contravariant vector. But the electric field is the gradient of the electric potential. If gradients are covariant, then shouldn't the electric field be an example of a covariant vector?

128.138.102.7 (talk) 01:32, 11 December 2009 (UTC)

The gradient usually means the contravariant components of the differential, and the electric field (as a proper gradient of the potential) is contravariant. There is some confusion both in the literature and this article about this point. Someone should definitely make an effort to fix it, if it can be done in a way that doesn't sacrifice understandability. (There is a section in the article gradient that attempts, but fails wildly, to shed any light on this problem.) Sławomir Biały (talk) 02:28, 11 December 2009 (UTC)

Comments and Compliments

I just want to say that, since the last time I've viewed this article (about a year ago), this article has improved dramatically! I am a Pure Math grad student, and "contravariance and covariance" of vectors was always a big mystery to me since the undergrad days. I had the sense that very few mathematicians actually understood what physicists meant by these terms. And I could not wrap my head around anything like "a geometric entity" and "a collection of numbers that change a certain way". These concepts seemed to vague to me. And reading this improved article now, I realize that the essence of "contravariance" and "covariance" were lost when everyone tried to explain it in the setting of local coordinates on manifolds, when in fact formalizing them in a general vector space first drives the essence home more clearly. And providing all the creature comforts of a mathematician with phrases like "Let V be a vector space over the field F". Now, the only question I have left is, what is gained by talking about "contravariance" and "covariance", rather than just vector spaces and their dual spaces? And does covariance and contravariance of vectors have any relation to the contravariant functor mapping a vector space V to its dual V*? --69.143.197.210 (talk) 14:22, 13 January 2010 (UTC)

New image

The new image does not seem to be helpful. At worst, it is either meaningless or misleading. I suggest that it should be removed. Sławomir Biały (talk) 02:31, 30 January 2011 (UTC)

Hi, could you please explain what you found "dubious" in that illustration of contravariant and covariant vectors that you removed? As far as one takes an orthogonal reference system, the difference between them is not so obvious, so I chose a skew system to show the essence of their difference. i.e. that in that case the cross product of two contravariant base vectors doesn't give the third contravariant, but respective covariant base vector etc. Was it that choice that irritated you? With regards --Qniemiec (talk) 14:06, 3 February 2011 (UTC)

In short, the image requires too much head-scratching and interpretation to make a useful image for the article (especially for the lead of the article). Apart from the issue that the image is not very aesthetically appealing, there are several more specific technical issues with it: (1) the use of nonstandard notation i,j,k refer to the unit vectors of a skew coordinate system, (2) the nonstandard labeling of the coordinate axes with x, y, z (hardly symbols one thinks of in connection with skew coordinates), (3) the lack of any connection with the text of the article (the relevant section is "Covariant and contravariant components of a vector", which uses a different notation than the image), (4) the fact that the image doesn't really illustrate what a covariant or contravariant vector is (a better image for this purpose is the one that appears just prior to "Covariant and contravariant components of a vector", although that one is also not aesthetically perfect), (5) the formulas given for the dual basis are wrong (in my opinion, they should be divided by the scalar triple product, although old-fashioned applied mathematics books keep track of the scalar coefficients separately for some reason). Sławomir Biały (talk) 15:28, 3 February 2011 (UTC)

Added small diagrams to illustrate co/contravariance in the examples given.

For a category theorist, a contravariant functor F would change a diagram $A\rightarrow B$ into $F(A)\leftarrow F(B)$, whereas a covariant functor G would change the diagram to $G(A)\rightarrow G(B)$, preserving the direction of the arrow. This is why I added similar (though informal) diagrams in the example, just to highlight this phenomenon. I hope someone can improve on my formatting, because I wasn't sure how to do it. I hope my idea is a helpful one, considering the little space it takes up.Rschwieb (talk) 00:00, 14 February 2011 (UTC)

Acceleration Contravariant?

Hi. I don't think position and acceleration are generally contravariant. For example, consider an object at the origin with a 2D transformation:

$\left(x'^{i}\right)=\left(x^{i}\right)+(1,0)$

The position becomes (1,0), but the transformation law demands

$x'^{i}={x'}_{j}^{i}x^{j}$

which gives (0,0). So position doesn't transform as a (1,0) tensor, and so is not contravariant. Also, if it were contravariant, then velocity wouldn't be (but it's easy to prove velocity always is).

I just finished a General Rel assignment where one question was to prove acceleration isn't contravariant. The example I gave was

$\left(x'^{i}\right)=\left(x^{2},y\right)$

with particle trajectory

$\left(x^{i}\right)=(t,0)$

This gives

${\begin{array}{lcl}(a^{i})&=&(0,0)\\a'^{i}&=&{\frac {d}{dt}}v'^{i}\\&=&{\frac {d}{dt}}{x'}_{j}^{i}v^{j}\\a'^{1}&=&{\frac {d}{dt}}2x\\&=&2\end{array}}$

Note the Jacobian has to be evaluated at the particle location. So $\left(a'^{i}\right)=(2,0)$. i.e. the object is accelerating, but the transformation law gives

$a'^{i}={x'}_{j}^{i}a^{j}=0$

So acceleration isn't a contravariant vector.

Tinos (talk) 13:42, 12 March 2011 (UTC)

Leaving aside general relativity, position measured with respect to an observer is contravariant. The coordinate change you have made is not linear: it moves the observer. It's true that this isn't contravariant under general coordinate transformations, but then it isn't meaningful to regard displacement as a vector anyway. For your second point, acceleration in GR is defined using the covariant derivative. It is not just the second derivative with respect to a parameter. It then becomes generally contravariant. The same is true in noninertial classical coordinate systems. Sławomir Biały (talk) 14:52, 12 March 2011 (UTC)

For example, consider writing the trajectory

$x=x_{0},y=-t^{2}$

in polar coordinates. The acceleration vector is not

$\theta ''{\frac {\partial }{\partial \theta }}+r''{\frac {\partial }{\partial r}},$

--Sławomir Biały (talk) 14:35, 13 March 2011 (UTC)

I agree. I'd add that position is a point in an affine space (or more generally, on a manifold), and so a position isn't really a vector or tensor at all. Vectors and tensors live in the tangent space of positions. I think that's what Sławomir means by saying that displacement isn't a vector. A vector can define a geodesic, but the displacement itself isn't a vector. —Ben FrantzDale (talk) 14:18, 14 March 2011 (UTC)

Do covariant components transform like basis vectors, or exactly like basis vectors?

A great many sources claim that covariant components transform exactly like basis vectors. Their equations seem to tell a different story.

The ubiquitous Jacobian form of the tensor transform laws[1] indicates the sum is taken on the lower index of the Jacobian for contravariant tensors, and the upper index of the inverse Jacobian for covariant tensors.

In other words, covariant components transform as the inverse transpose of the contravariant components.

The article says: "If the contravariant basis vectors are orthonormal then they are equivalent to the covariant basis vectors". Under orthogonal transformations (such as a 45° rotation), the covariant and contravariant components remain identical. If the covariant components transformed inversely to the contravariant components as claimed in the article, vectors and covectors would rotate in opposite directions, their components would not remain identical.

Orthogonal transformations by definition are equal to their inverse transpose. Loosely speaking, taking the transpose of a matrix reverses its direction of rotation. Taking the inverse of a transposed matrix returns its original sense of rotation and inverts its scale. Loosely, covectors tend to rotate with vectors but scale reciprocally. NOrbeck (talk) 23:03, 19 May 2011 (UTC)

I'm not sure exactly what point in the text this perceived contradiction is supposed to occur. A basis is naturally regarded in the article as an invertible linear map $\mathbf {f} :\mathbf {R} ^{n}\to V$. The covariant components of $\alpha \in V^{*}$ are given by the linear form $\alpha \circ \mathbf {f} \in (\mathbf {R} ^{n})^{*}$, $\alpha \circ \mathbf {f} :\mathbf {R} ^{n}\to \mathbf {R}$. A change of basis is an element A of GL(n), which composes on the right with f to give a new basis $\mathbf {f} '=\mathbf {f} \circ A$, and the components of a covector $\alpha$ transform via $\alpha '=\alpha \circ A$ (note this is by exactly the same transformation as the change of basis $\mathbf {f} '=\mathbf {f} \circ A$). One can certainly also write this as $A^{T}\alpha$, where $A^{T}$ is the transpose of A (by definition of the transpose of a linear map).

This is also clear in the Einstein summation convention, where a basis undergoes a transformation of the form

$\mathbf {e} _{i}'=\mathbf {e} _{i}A_{j}^{i}$

and the components of a covector undergo precisely the same transformation:

$\alpha _{i}'=\alpha _{i}A_{j}^{i}.$

In either point of view, the transformation is exactly the same as that undergone by the basis vectors.

By contrast, a contravariant vector has components given by $\mathbf {f} ^{-1}(v)$, and this transforms via

$A^{-1}\mathbf {f} ^{-1}v.$

--Sławomir Biały (talk) 14:41, 30 May 2011 (UTC)

Thank you for the detailed response. The problem seems to be ambiguous notation. $\alpha _{i}A_{j}^{i}$ could mean either:

$A_{j}^{\ i}\alpha _{i}=[A]\alpha$, or

$A_{\ j}^{i}\alpha _{i}=[A]^{\mathrm {T} }\alpha$

The second equation is correct. This can be verified by direct calculation using the data from the worked example:

${\begin{bmatrix}2&{\sqrt {1/2}}\\0&{\sqrt {1/2}}\end{bmatrix}}^{\mathrm {T} }{\begin{bmatrix}3+{\sqrt {2}}\\{\sqrt {2}}\end{bmatrix}}={\begin{bmatrix}6+2{\sqrt {2}}\\2+3/{\sqrt {2}}\end{bmatrix}}$

To see this geometrically, consider a 45° rotation of the standard basis, the components of vectors and covectors transform identically, and they both transform inversely to the basis vectors.

OpenGL's conventions provide a clear and succinct formalism. Let all vectors and covectors be represented as column matrices. Arrays of vectors/covectors are represented as matrices where each element is a column of the matrix. Let A be the change of basis matrix, let e_i be the matrix of basis vectors, and Θⁱ be the matrix of basis covectors. The transformation laws are as follows:

	Basis vectors:	ei ' = A ei
	Components of 1-forms:	α' = AT α
	Components of vectors:	v' = A-1 v
	Basis covectors:	Θi ' = (AT)-1 Θi

There are four transformations, corresponding to the four types of objects. This formalism has many advantages, and is hard-coded in GPU hardware and graphics APIs. See: pg 3 [2] [3] pg 29. It is common when performing Blinn-Phong illumination to mis-transform the normals, which causes surfaces facing light sources to be dim, while saturating perpendicular surfaces, see the DirectX documentation TranformNormal, contrast with TransformCoordinate. NOrbeck (talk) 00:01, 4 June 2011 (UTC)

The basic assumption that elements of V are column vectors is problematic. The elements of V could be velocities, electromagnetic fields, tangent vectors to manifolds, etc. The entire point of the formalism is that it does not need to specify the nature of the elements of V. Thus your first equation $e_{i}'=Ae_{i}$ is a non-starter. To make sense of it, A must be an endomorphism of V, whereas the next two equations you write require A to be a numerical matrix. Sławomir Biały (talk) 00:10, 4 June 2011 (UTC)

Non-integer powers?

I've been thinking about the covariance matrix. In particular, the covariance matrix for a position estimate is a type-(2,0) tensor in that it comes from the tensor product of vectors. Now, the matrix square root of the covariance matrix is useful, for example, for generating a multivariate normal distribution you multiply vectors drawn from the standard normal distribution by the square root of the covariance matrix. So, what is the type of the matrix square root of a type-(2,0) matrix? It seems like it transforms with the square root of the transform. That is,

$(T\Sigma T^{\top })^{1/2}=T^{1/2}\Sigma ^{1/2}T^{\top 1/2}$

Is there language for this? —Ben FrantzDale (talk) 01:02, 29 May 2011 (UTC)

The square root of a matrix isn't multiplicative (i.e., ${\sqrt {AB}}\not ={\sqrt {A}}{\sqrt {B}}$), to say nothing of the fact that the square root may not be unique. The equation you've written doesn't appear to be true in general. Sławomir Biały (talk) 13:55, 30 May 2011 (UTC)

I'll have to think about that. Thanks. —Ben FrantzDale (talk) 19:56, 30 May 2011 (UTC)

Archive 1

Proposed split

As it is currently written, the section on covariant and contravariant components of a vector is only of peripheral relevance to the subject of this article. Indeed, it only makes sense to talk about covariant and contravariant components of the same vector in an inner product space, whereas the article ought to be about the general transformation law. Moreover, there is actually more bookkeeping necessary to discuss co/contravariant components, because there is a change of basis to go from the contravariant components to the covariant components, and then an additional change of basis when one changes the original background basis. This seems likely to add to the confusion inherent in what is already a difficult subject for people to grasp. I propose to split out the section on covariant and contravariant components of a vector to a different article, and leave a summary of the relevant content here. Sławomir Biały (talk) 14:01, 30 May 2011 (UTC)

Merge?

I see that a number of related articles now support merge tags. (One might also add covariant transformation to the mix.) I'm not opposed to a merge, but this needs to be discussed somehow. A blind merging of content into one article would almost certainly be a bad idea. What does the envisioned new configuration of content look like? Sławomir Biały (talk) 14:26, 24 August 2011 (UTC)

Usage in tensor analysis

First and third paragraphs have no information. Second paragraph explains about how a metric induces an isomorphism non-canonically, but is needlessly vague and wordy. --MarSch 14:38, 24 Jun 2005 (UTC)

States "Note that in general, no such relation exists in spaces not endowed with a metric tensor." I'm pretty certain this isn't true. Horn.imh (talk) 18:24, 13 February 2012 (UTC)

More completely, from the article:

When the manifold is equipped with a metric, covariant and contravariant indices become very closely related to one-another. Contravariant indices can be turned into covariant indices by contracting with the metric tensor. Contravariant indices can be gotten by contracting with the (matrix) inverse of the metric tensor. Note that in general, no such relation exists in spaces not endowed with a metric tensor.

It seems accurate to me. You cannot constract with a tensor that does not exist. You may be confusing this with the existence of covariant and contravariant bases, and the contraction of covariant with contravariant indices, which requires no metric tensor. — Quondum^☏✎ 18:50, 13 February 2012 (UTC)

colour image

At some requests I re-coloured the image [[file:Basis.png]]. Please revert it you think its better before. F = q(E+v×B) ⇄ ∑_ic_i 19:58, 3 April 2012 (UTC)

Change of basis vs. change of coordinate system

There seems to be a misconception (more correctly, an implied assumption) that is propagated by this article and others, which is in effect that the basis on a differentiable manifold must be holonomic, also called a coordinate basis. While a use of a holonomic basis is mathematically convenient, despite its predominant use it is by no means necessary. In particular, we can define a (generally non-holonomic) basis for the tangent space of a manifold in an arbitrary fashion (i.e. independently at every point on the manifold), and the concept of covariance and contravariance still applies. It applies for any tensors, and is unrelated (other than by convention) to their being tensor fields.

Thus, in an article such as this one, it would be appropriate to write in terms of simply a basis, and not in terms of a coordinate basis or coordinate system, as the former is far more general. Why I feel it is important is illustrated by my own experience: it took me decades to figure out why the connection between a coordinate system and co-/contravariance seemed inexplicably obscure, only to discover that it is merely a convenient convention and not a mathematical necessity. Let's avoid perpetuating this type of misconception, by rewording this and related articles accordingly. — Quondum^☏ 11:12, 29 July 2012 (UTC)

I think that changes in coordinate systems are likely to be easier to understand to the casual reader, and I would like to see the lead emphasizing these rather than changes in bases. The issue of non-holonomic bases can certainly be mentioned, but I don't think it needs to be a centerpiece. Sławomir Biały (talk) 14:19, 29 July 2012 (UTC)

Added an illustration (referenced) and summary (from talk:Ricci calculus)...

So revert if it doesn't help. Maschen (talk) 08:04, 3 September 2012 (UTC)

Momentum and force

I have removed momentum and force from the list of examples of contravariant vectors because there are some who say they ought to be considered covariant instead. Some of the arguments for that position include the work equation

$W=\int F_{i}dx^{i}$,

the Lagrangian formulation

$p_{i}={\frac {\partial L}{\partial {\dot {x}}^{i}}}$,

and that many forces arise as the gradient of a potential. If you think this is worth mentioning in the article, there's further discussion of this topic on the Physics Forums website here, including some references to sources. -- Dr Greg  talk  01:40, 1 February 2013 (UTC)

That seems fine to me. Sławomir Biały (talk) 01:16, 5 February 2013 (UTC)

This article is a little confusing to a mathematician

I do pure differential geometry not physics, and I imagine that part of my confusion may come from differences in notation and conventions. But I'd like to point out a few things that are confusing to a pure mathematician. These are probably not the same things that are confusing to a student. So you can do with them what you will.

From my perspective, the only real thing to say is that contravariant vectors are those we choose to be in our space, and covariant vectors are those in the dual space. If $v$ is a vector in our space and $A$ is a linear transformation of our space, then the usual action of $A$ on $v$ is via left matrix multiplication: $v\mapsto Av$. On the other hand, if $w$ is a linear functional (so an element of the dual space) it is represented as a row vector. We can treat column vectors as linear functionals via the inner product pairing $\langle w,v\rangle =w^{\dagger }v$. Here dagger means transpose. This associates the column vector $w$ with the row vector $w^{\dagger }$. Now it is clear that $A$ also acts on the dual space (the row vector space) via the transpose. That is, there is a map $\dagger$ that eats a linear transformation of our vector space and spits out a linear transformation of the dual space. The transpose acts on the right in the dual space. $w^{\dagger }\mapsto w^{\dagger }A^{\dagger }$. Acting on the right reverses arrows, which physicists traditionally call covariant. So the entire difference is that matrices act on vectors on the left and covectors on the right.

But none of this is explicit in the article. I get the feeling that the article is attempting to hide these details -- perhaps for fear that they're confusing to students. But in the effort to attempt to be intuitive, a great deal of confusion is introduced.

For example:

• The article says that the usage in physics is a specific example of the corresponding notions in category theory. Are we quite sure this is right? It seems more like the notions are exactly opposite as they are in category theory. In physics, a contravariant operation preserves arrows and a covariant operation reverses arrows (that is, contravariant means transformations act on the left while covariant means they act on the right). This is the opposite of the usage in category theory.
• Is it sensible to refer to vectors or covectors as "basis independent"? I'm pretty sure you mean that the notation is basis independent, not the vector.
• What does it mean for a vector to have contravariant components? The component of a vector in this article are real numbers. Can real numbers sensibly be said to be contravariant or covariant?
• The article says

the transformation that acts on the vector of components must be the inverse of the transformation that acts on the basis vectors.

but it's unclear how to make sense of this. You have an object from a group $A$ acting on an object $v$. Once you specify how $A$ acts on $v$ there's no room to say "oh but it acts on certain subsets of $v$ in a completely different way." In fact the action $Av=v_{1}Ae_{1}+v_{2}Ae_{2}+v_{3}Ae_{3}$ is entirely determined by the action on the basis by linearity. I assume what the article is trying to convey is that if you switch to a ruler where the markings are twice as far apart, you need to half your measurements to compensate. But speaking about an action as if it acts on some parts of a set one way and other parts of the same set another way just doesn't make any sense.

• The article uses the same basis $f$ for vectors and for covectors. That means that both row vectors and column vectors are linear combinations of the same vectors, which makes no sense. I assume you mean that you can associate linear functionals to column vectors. But you should say this explicitly. Essentially the whole point of the contravariance/covariance concept in this case is that the mapping from dual vectors to vectors reverses arrows. If you do that mapping *implicitly* by pretending they are in the same vector space, then you're doing a disservice to the reader.
• Even more confusingly, the same basis is used in column vector notation *and* row vector notation. What I am referring to is the notation following "Denote the column vector of components of v by..." and "Denote the row vector of components of $\alpha$ by...". It would be more clear to decide that f is a basis for, say, the vector space, and that g is the dual basis in the dual vector space. Using the same symbol for two objects is a bit confusing in this context.
• The article says

a triple consisting of the length, width, and height of a rectangular box could make up the three components of an abstract vector, but this vector would not be contravariant, since rotating the box does not change the box's length, width, and height.

But again it's hard to make any sense of this. The article discusses vectors and transformations on those vectors. So the relevant question is what happens to the length, width, and height if you do a rotation in the length-width-height vector space, not what happens if you rotate the box in a different vector space. It's a mixed metaphor that is likely to be confusing to readers. It makes about as much sense as saying that a giraffe's height is not a positive number because if you square its age it doesn't affect its height.

• There are several other examples, such as "The dual space of a vector space is a standard example of a contravariant functor". I assume what you mean is that the functor that sends a vector space to its dual, and which sends a linear map to the induced map on the dual space is contravariant. But a space is not a functor and vice versa. I think there is actually more than meets the eye to this point, because I would hazard a guess that a lot of what makes the article opaque is attempting to interpret facts about *transformations* as facts about *spaces*.

I think there is a lot that can be done to clarify the article. First, it would help a great deal to say what it means for the coordinates of a transformation to change in a different way than the basis. This notion is extremely vague and I think it is the source of a lot of mixed metaphors and confusing statements in the article. I would put in symbols what exactly this means. Either through a specific numerical example or using variables. Something like this deserves to go at the top before you say much more about coordinates transforming differently than bases.

In addition, I think the article could use some cleaning up of the notation. The odd bracket notation $v^{i}[f]$ should be explained explicitly. I've only come across this in introduction to linear algebra textbooks and it always causes a great deal of confusion to students. I don't have a suggestion for a better notation, but even that notation would work better with an explanation of what the bracket f is doing in there. In addition, if the Einstein summation convention is to be used, it should be used consistently.

Finally, I would suggest going through the entire article and making sure the authors are clear about

• What vector space we are working with in each sentence, and
• When we are switching from the space to the dual space.

I understand these spaces are naturally isomorphic, and that they are in practice often conflated. But a little pedantry can sometimes go a long way in making sure the ideas are expressed with precision and clarity. 50.181.78.116 (talk) 15:54, 30 April 2014 (UTC)

This is quite a lot of TLDR. The article is perfectly consistent as written. As a mathematician, you might find the following somewhat clarifying. If V is a vector space, then a basis of V can be identified with an invertible linear map from R^n to V. The set F of all bases is equipped with a natural right action of GL(n) by function composition. If f is an element of F, then the components of a vector v in V in the basis f are given by $f^{-1}(v)\in R^{n}$. So the right action of an element A of GL(n) on F goes over to the action of $A^{-1}$ on the components of v. Hence "the components of a vector transform contravariantly." I should emphasize that A is in GL(n), not GL(V), which is apparently the chief source of your confusion. Notice also that the vector v does not depend on the basis, only the components of the vector do. I am puzzled by your claim that this is not a sensible statement.

Finally, I've gone through a few of the things that you feel should be stated explicitly, and found that they are. For example, the notation v[f] and α[f] are both rigorously defined in the "Definition" section. I suggest that we try to condense your objections to the article down to something a little more digestible after a more careful reading of what is actually written, in the light of my (hopefully clarifying) remarks. Sławomir Biały (talk) 18:20, 30 April 2014 (UTC)

I have rewritten much of the section on "Algebra and geometry". I think this section was unnecessarily confusing, since it referred to covectors as contravariant and vectors as covariant, apparently because the spaces of these are contravariant and covariant functors (respectively) of the category of smooth manifolds. I have clarified what was intended by this. I have also removed some dead weight from the lead of the article that seemed to be a little misguided and confusing. Sławomir Biały (talk) 12:41, 1 May 2014 (UTC)

Gradient is a dual vector?

Second paragraph states that the gradient is an example of a dual vector. The gradient is a tangent vector, its the differential of a function f, df, that is a covector. In fact, the gradient is defined most generally to be the vector in the tangent space such that its < grad f, v > = df(v) for all v in the tangent space. — Preceding unsigned comment added by 108.3.139.48 (talk) 22:56, 14 February 2015 (UTC)

It depends on individual conventions whether the gradient is regarded as a vector or a covector. The components of the gradient in a tangent basis do transform covariantly, which is made clear in the introduction section. Sławomir Biały (talk) 02:01, 15 February 2015 (UTC)

"Most generally" a metric tensor or inner product (if that is what was meant by the symbol < , >) may not be not defined, yet grad f can (AFAICT) be defined as a covector on any differentiable manifold. This observation is presumably not dependent on convention. —Quondum 02:56, 15 February 2015 (UTC)

Yes, I agree that this is mainly a issue of definitions, i.e., how exactly you define the term "gradient." And from what I see it seems to be a difference between the physics and math community (my Differential Geometry background is from the math point of view). But saying that the gradient is a cotangent vector just doesn't make sense as a generalization of the "usual calc definition of gradient": the vector that you can dot with a direction to get the directional derivative. I think that most math texts / papers call what is defined in the article as the gradient (and alluded to above) as the "differential df." It is exactly df = (df/dx) dx + (df/dy) dy + (df/dz) dz, where the dx, etc are the usual basis for the cotangent space. Then as Quondum notes above, and as I stated, in the presence of a Riemannian metric you can identify the gradient, which is that element of the tangent space that, when you dot with another tangent vector, you get the *same value* as df(v). What I am saying here is in line with the entry "Gradient" which defines the gradient as: "The gradient of f is defined as the unique vector field whose dot product with any vector v at each point x is the directional derivative of f along v." Breaking this down: the gradient is a *vector field* (not cotangent vector field), and of course the v's they are referring to are tangent vectors (surely we are not thinking of the "directions" v as cotangent). You cannot take a dot product of a cotangent vector with a tangent vector, they are in different vector spaces, so that is another way in which it is consistent with the usual definiton to say the gradient is in the tangent space. — Preceding unsigned comment added by 108.3.139.48 (talk) 16:36, 15 February 2015 (UTC)

Actually the more I read the entry on "Gradient" the more I see it explains everything I'm saying (in the usual Euclidean case) much more clearly than I am doing. — Preceding unsigned comment added by 108.3.139.48 (talk) 16:39, 15 February 2015 (UTC)

It's definitely an issue that should be fixed if possible. The gradient is typically used in covector-ish ways in the sciences. As I see it, a significant problem is that "differential", while strictly more correct, might easily not be as widely understood to persons familiar just with vector calculus (as it is now taught in many universities). Perhaps something like "For example, the gradient of a function (or, more precisely, its differential) is a covector." But this might be seen as trying to gloss over the distinction between vectors and covectors. Sławomir Biały (talk) 17:12, 15 February 2015 (UTC)

Perhaps it is not that difficult to deal with, perhaps primarily in the Gradient article: what is needed is to make it clear that there are two inequivalent definitions. In this article, all that is needed is to indicate that we are using only one of two definitions. —Quondum 18:36, 15 February 2015 (UTC)

Informal usage

The example in this section is badly chosen. The Schrödinger equation is invariant under the symmetry transformations of Newtonian spacetime, because that's the spacetime in which it is formulated. Of course it is not invariant under Lorentz transformations then.--5.61.170.128 (talk) 23:08, 26 March 2015 (UTC)

confused about notation

Hi. Sorry if this is discussed above, but after a quick read of this article I'm confused by what (to me) seems like a switch in terms between the 2d example under Euclidean plane, and the very next paragraph Three D Euclidean plane. In the former the vector V has (contravariant) components 3/2,2 .. I assume that's therefor a 'contravariant vector', and uses e_1, e_2 as basis (correct me if I'm wrong there). But then in the 3D paragraph the 'contravariant (dual) basis' vectors are indexed with e^1, e^2, e^3 i.e. upper index as opposed to lower index...?! Are the components and the basis actually different naming conventions... one is contravariant and one covariant for the same 'covariant vector'? If the notation *is* correct here then could someone please add some explanation so as to clear this up as it's very confusing to the non-initiated. Thanks. S — Preceding unsigned comment added by 203.110.235.6 (talk) 23:31, 22 August 2016 (UTC)

Not sure what the best way to clarify this in the article is. If the components of a vector transform contravariantly, then the basis itself transforms covariantly to compensate. Thus the vector $v=\sum \mathbf {e} _{i}v^{i}$ is invariant, because the components $v^{i}$ transform contravariantly, and the vectors $\mathbf {e} _{i}$ transform covariantly. To extract the (contravariant) components $v^{i}$, we must dot with the dual basis $\mathbf {e} ^{i}$. This basis transforms contravariantly, and so is often called a contravariant basis. Sławomir
Biały 12:48, 23 August 2016 (UTC)

Velocity is contravariant wrt distance and covariant wrt time

Velocity = distance per time = d/t

Velocity is contravariant with respect to distance (as stated in the article). But velocity is covariant with respect to time.

Just granpa (talk) 19:27, 28 May 2017 (UTC)

acc = d/t^2

3600 meter/minute^2 = 1 meter/sec^2

Just granpa (talk) 03:24, 29 May 2017 (UTC)

Contravariant

I agree with others that the notation is distracting. As an offering for debate I submit the following for the explanation of contravariant.

The Einstein summation convention is used; for emphasise only $k$ is used as the dummy summation index.

An arbitrary point in ${\mathcal {R}}^{n}$ has coordinates ${\textbf {p}}_{O}=(p^{1},\cdots ,p^{n})$. Introduce any basis vectors $X=\{{\textbf {x}}_{1},\cdots ,{\textbf {x}}_{n}\}$, with ${\textbf {x}}_{j}=(x_{j}^{1},\cdots ,x_{j}^{n})$, which generate coordinate vectors ${\textbf {p}}_{X}=(v^{1},\cdots ,v^{n})$, such that ${\textbf {p}}_{O}=v^{k}{\textbf {x}}_{k}$ and hence $p^{i}=x_{k}^{i}v^{k}$. In matrix notation ${\textbf {p}}_{O}={\textbf {B}}_{X}{\textbf {p}}_{X}$ with $x_{j}^{i}$ the $(i,j)$ element of matrix ${\textbf {B}}_{X}$ and ${\textbf {p}}_{O}$, ${\textbf {p}}_{X}$ treated as column vectors.

Alternative basis vectors $E=\{{\textbf {e}}_{1},\cdots ,{\textbf {e}}_{n}\}$ with ${\textbf {e}}_{j}=(e_{j}^{1},\cdots ,e_{j}^{n})$ generating ${\textbf {p}}_{E}=(r^{1},\cdots ,r^{n})$ such that ${\textbf {p}}_{O}=r^{k}{\textbf {e}}_{k}$, $p^{i}=e_{k}^{i}r^{k}$, ${\textbf {p}}_{O}={\textbf {B}}_{E}{\textbf {p}}_{E}$.

Write ${\textbf {e}}_{j}=a_{j}^{k}{\textbf {x}}_{k}$ then $e_{j}^{i}=x_{k}^{i}a_{j}^{k}$ and ${\textbf {B}}_{E}={\textbf {B}}_{X}{\textbf {A}}$ with $e_{j}^{i}$, $a_{j}^{i}$ the $(i,j)$ element of matrices ${\textbf {B}}_{E}$, ${\textbf {A}}$.

From ${\textbf {B}}_{X}{\textbf {p}}_{X}={\textbf {B}}_{E}{\textbf {p}}_{E}={\textbf {B}}_{X}{\textbf {A}}{\textbf {p}}_{E}$ then ${\textbf {p}}_{X}\mapsto {\textbf {p}}_{E}$ is given by ${\textbf {p}}_{E}={\textbf {A}}^{-1}{\textbf {p}}_{X}$ and hence $X\mapsto E$ is a contravariant transformation.

This is simplistic, requires only elementary understanding of a vector, but still leaves elementary manipulations to the reader. It ties in with the idea of a matrix as a transformation and leads into the more difficult concepts of a dual space, covariant transformations and tensors. The notation is consistent with elementary tensor notation. — Preceding unsigned comment added by PatrickFoucault (talk • contribs) 09:52, 14 September 2017 (UTC)

Organisation

I advocate the article be organised along the following lines.

• A very brief heuristic introduction about components transforming contra or co to the basis
• Brief history and etymology sections
• The above demonstration that a position vector always transforms contra. This also introduces the agreed notation.
• A similar demonstration regarding a vector that we would like to transform co
• Statement and link regarding the dual space and linear functionals
• Demonstration of a co transformation using a specific linear functional which should be the dot product.
• Discussion and links regarding tangents and normals and their use as bases.
• Mention of how this develops into tensors with links.

The demonstrations should be clear about the exact transformations. The current article is good, but it seems from the talk that further clarity is required. I think some of the introduction could be trimmed in favour of detailed worked examples of contra and co transformations. The current description of a covariant transformation could be clearer, and would benefit by being couched in terms of a specific functional such as the dot product, and possibly along the lines of the above contravariant demonstration. This would allow the concepts of row space and column space to emerge naturally and hence links to these articles. The inherent difference between contravariant and covariant is exposed without relying on heuristic explanations using tangents and normals.Foucault (talk) 03:52, 15 September 2017 (UTC)

Your addition was entirely wp:unsourced wp:original research. It does not comply with MOS:LEAD either. I have reverted it, for obviouis reasons. - DVdm (talk) 08:34, 16 September 2017 (UTC)

@Foucault: I have not read your attempt in detail, but you cannot ignore the map that sends a contravariant vector to a covariant vector and vice versa. In Lorentz transformation#Covariant vectors you can find a similar overview (equally unsourced, but sourcable) in the special case that the map in question is the Lorentz metric. YohanN7 (talk) 10:37, 16 September 2017 (UTC)

It is not my intention to ignore that map, nor my intention to write a definitive study. From the talk above, it seems some people feel the article could be improved. My attempt was at writing an introduction that would draw readers into reading further and also spark editors into making further constructive edits. If my attempt sparks activity, then good. The alternative is the article remains moribund.Foucault (talk) 02:48, 18 September 2017 (UTC)

I don't share your rigid verdict of this article being moribund, but of course, it is improvable. My two cents on possible improvement are that with all the usual considerations on "invariance to co- and contravariant transformations" between two frames/vectors, there is a third frame, camouflaged in the backdrop, most often. I think, e.g., all pictures of such frames (Euclidean or curvilinear) necessarily rely on this "observer's frame", and active and passive transformations might thus be judged from an other, possibly alien space. Purgy (talk) 06:13, 18 September 2017 (UTC)

OK. Not moribund. It has a B rating, is high priority and is in the top 500 articles viewed. So it seems the subject is worthwhile, a lot of good work has already gone into the article, but contributers to this talk page are still debating what the words contravariant and covariant mean. Foucault (talk) 10:04, 18 September 2017 (UTC)

Math under Three-dimensional Euclidean Space

Can someone look into this?

While reading the following part,

Then the covariant coordinates of any vector v can be obtained by the dot product of v with the contravariant basis vectors: $q_{1}=\mathbf {v} \cdot \mathbf {e} ^{1};\qquad q_{2}=\mathbf {v} \cdot \mathbf {e} ^{2};\qquad q_{3}=\mathbf {v} \cdot \mathbf {e} ^{3}.$
Likewise, the contravariant components of v can be obtained from the dot product of v with convariant basis vectors, viz.: $q^{1}=\mathbf {v} \cdot \mathbf {e} _{1};\qquad q^{2}=\mathbf {v} \cdot \mathbf {e} _{2};\qquad q^{3}=\mathbf {v} \cdot \mathbf {e} _{3}.$

I thought the math should have been this instead.

Then the covariant coordinates of any vector v can be obtained by the dot product of v with the contravariant basis vectors: $q_{1}=\mathbf {v} \cdot \mathbf {e} _{1};\qquad q_{2}=\mathbf {v} \cdot \mathbf {e} _{2};\qquad q_{3}=\mathbf {v} \cdot \mathbf {e} _{3}.$
Likewise, the contravariant components of v can be obtained from the dot product of v with convariant basis vectors, viz.: $q^{1}=\mathbf {v} \cdot \mathbf {e} ^{1};\qquad q^{2}=\mathbf {v} \cdot \mathbf {e} ^{2};\qquad q^{3}=\mathbf {v} \cdot \mathbf {e} ^{3}.$

But then, the following makes even less sense. It would couple the covariant (contravariant) coordinates to one another through the covariant (contravariant) bases.

and we can convert from contravariant to covariant basis with $q^{i}=\mathbf {v} \cdot \mathbf {e} _{i}=(q^{j}\mathbf {e} _{j})\cdot \mathbf {e} _{i}=(\mathbf {e} _{j}\cdot \mathbf {e} _{i})q^{j}$
and $q_{i}=\mathbf {v} \cdot \mathbf {e} ^{i}=(q_{j}\mathbf {e} ^{j})\cdot \mathbf {e} ^{i}=(\mathbf {e} ^{j}\cdot \mathbf {e} ^{i})q_{j}.$

D4nn0v (talk) 08:38, 29 November 2017 (UTC)

I tried to fix the problem. Let me know, if you see anything I missed or disagree with what I did. JRSpriggs (talk) 02:18, 30 November 2017 (UTC)

Looks good! D4nn0v (talk) 02:16, 4 December 2017 (UTC)

Confusion between vector components, vector coordinate and the reference axes.

In the second paragraph under Introduction of there are too many undefined terms which are very confusing. While the component of the vector are the <v₁,v₂,v₃> and the reference axis is given to mean the coordinate basis vector, its not clear what does the word "coordinate" refers to. From the example involving the change of scale of the reference axis, it's quite easy to understand what how the components of the vector vary inversely to change of scale of the basis vectors. But the second paragraph under Introduction states that components of contravariant vectors vary inversely to the basis vector(which is clearly understood) but "transform as the coordinates do". What do coordinates mean here? the coordinate of the vector which or the coordinate axis?. The word coordinate has been used multiple times without an explanation as to what it means while it is not at all required as the concept is clear by stating how the components change with the change of basis(ie the reference axes).

granzer92 Granzer92 (talk) 14:09, 10 June 2018 (UTC)

I removed some misinformation from the lead and the introduction. I hope that helps.

The coordinate system on a manifold generally determines the choice of basis vectors for the tangent space at each point on the manifold. That is why it is relevant. JRSpriggs (talk) 02:33, 11 June 2018 (UTC)

Standard definition apparent inconsistency

Could someone please explain the fallacy in the following?

Suppose that in $\mathbf {R} ^{3}$ we change from a basis $B$ in units of meters to a basis ${\overline {B}}$ in units of centimeters. That is,

$\mathbf {\overline {b}} ^{i}=\left({\frac {1}{100}}\right)\mathbf {b} ^{i},\quad (1\leq i\leq 3).$

Then the coordinate transformation is

${\overline {x}}^{i}=(100)x^{i},\quad (1\leq i\leq 3),$ (1)

and the coordinate transformation in matrix form is

$\mathbf {A} ={\begin{pmatrix}100&0&0\\0&100&0\\0&0&100\end{pmatrix}}.$ (2)

A position vector

$\mathbf {r} =3\mathbf {b} ^{1}+4\mathbf {b} ^{2}+12\mathbf {b} ^{3}$ (3)

with magnitude $|\mathbf {r} |=13{\text{ m}}$ is transformed to

$\mathbf {\overline {r}} =300\mathbf {\overline {b}} ^{1}+400\mathbf {\overline {b}} ^{2}+1200\mathbf {\overline {b}} ^{3}$ (4)

with magnitude $|\mathbf {\overline {r}} |=1300{\text{ cm}}.$

Suppose that a scalar function $f(x^{i})=-2{x}^{1}$ is defined in a region containing r. Then,

${\frac {\partial {f}}{\partial {{x}^{1}}}}=-2,{\frac {\partial {f}}{\partial {{x}^{2}}}}={\frac {\partial {f}}{\partial {{x}^{3}}}}=0,$ (5)

the gradient vector is

$\mathbf {\nabla {f}} ={\frac {\partial {f}}{\partial {{x}^{1}}}}\mathbf {b} ^{1}+{\frac {\partial {f}}{\partial {{x}^{2}}}}\mathbf {b} ^{2}+{\frac {\partial {f}}{\partial {{x}^{3}}}}\mathbf {b} ^{3}=-2\mathbf {b} ^{1},$ (6)

and the gradient vector at r,

$\mathbf {\nabla {f}} (\mathbf {r} )=-2\mathbf {b} ^{1},$ (7)

with magnitude $|\mathbf {\nabla {f}} (\mathbf {r} )|=-2{\text{ m}}^{-1}$, is transformed to

$\mathbf {\overline {\nabla {f}}} (\mathbf {\overline {r}} )=-0.02\mathbf {\overline {b}} ^{1},$ (8)

with magnitude $|\mathbf {\overline {\nabla {f}}} (\mathbf {\overline {r}} )|=-0.02{\text{ cm}}^{-1}.$

While the position vector r and the gradient vector $\mathbf {\nabla {f}} (\mathbf {r} )$ are invariant, the components of the position vector in equations (3) and (4) transform inversely as the basis vectors, and the components of the gradient vector in equations (7) and (8) transform directly as the basis vectors.

Now, most textbooks agree that a vector u is a contravariant vector if its components $(T^{i})$ and $({\overline {T}}^{i})$ relative to the respective coordinate systems $(x^{i})$ and $({\overline {x}}^{i})$ transform according to

${\overline {T}}^{i}=T^{r}{\frac {\partial {{\overline {x}}^{i}}}{\partial {x^{r}}}},\quad (1\leq i\leq 3)$ (9)

and that a vector w is a covariant vector if its components $(T_{i})$ and $({\overline {T}}_{i})$ relative to the respective coordinate systems $(x^{i})$ and $({\overline {x}}^{i})$ transform according to

${\overline {T}}_{i}=T_{r}{\frac {\partial {x^{r}}}{\partial {{\overline {x}}^{i}}}},\quad (1\leq i\leq 3),$ (10)

but equations (4) and (8) seem to indicate the exact opposite of equations (9) and (10). Why?—Anita5192 (talk) 17:44, 24 November 2018 (UTC)

There is an error in your comment right at the beginning. So I stopped reading it at that point. If $x^{i}$ is the position in meters and ${\overline {x}}^{i}$ is the position in centimeters, then the conversion is just:

${\overline {x}}^{i}=100\cdot x^{i},\quad (1\leq i\leq 3).$

OK? JRSpriggs (talk) 22:46, 24 November 2018 (UTC)

The $x^{i}$, with $|x^{i}|=1{\text{ m}}$, are the old basis vectors; the ${\overline {x}}^{i}$, with $|{\overline {x}}^{i}|=0.01{\text{ m}}=1{\text{ cm}}$ are the new basis vectors.—Anita5192 (talk) 03:17, 25 November 2018 (UTC)

Maybe this helps:

Let's have two ordered bases of a 3-D vector space over $\mathbb {R} ,$ consisting of three orthogonal vectors each

$\{e_{i}\mid i\in \{1,2,3\}\}\quad$ and $\quad \{{\bar {e}}_{i}\mid i\in \{1,2,3\}\}\quad$ with

$||e_{i}||=1{\text{m}}\quad$ and $\quad ||{\bar {e}}_{i}||=1{\text{cm}}\quad$ for $i\in \{1,2,3\}.$ (To be honest, I am unsure how to formally conflate a multiplicative group of units with the norm of the vector space)

Further, let (for simplicity, and satisfying the above)

${\bar {e}}_{i}={\frac {1}{100}}e_{i},\quad$ again for $i\in \{1,2,3\}.$

This yields the matrix $A$ from above. Now let's have a vector, and its decompositions wrt the two bases (adopting Gaussian summation convention)

$r=r^{i}e_{i}={\bar {r}}^{i}{\bar {e}}_{i}.$

For the last equalities to hold, the scalar coefficients must satisfy

${\bar {r}}^{i}=100r^{i}\quad$ for $i\in \{1,2,3\}.$

This yields the relation for coefficients, given by JRSpriggs above. Maybe it's all about the vectors, formed from the coefficients suitably arranged in tuples (and freely identified with abstract vectors) that vary contravariantly? (I'm struggling myself.)

OK? Purgy (talk) 13:14, 25 November 2018 (UTC)

This makes perfect sense to me, and I believe this is what I wrote in equations (1,2,3,4), but I do not see how equations (9,10) agree with this. For example, equation (1) seems to imply that for the basis vectors, $x^{i}$ and ${\overline {x}}^{i}$,

${\frac {\partial {{\overline {x}}^{i}}}{\partial {x^{i}}}}={\frac {1}{100}},\quad (1\leq i\leq 3)$ (11)

(the other partial derivatives are zero), but then equation (9) for the components $(T^{i})$ and $({\overline {T}}^{i})$ of $(\mathbf {r} )$ and $(\mathbf {\overline {r}} )$ would be

${\overline {T}}^{i}=T^{i}{\frac {1}{100}},\quad (1\leq i\leq 3),$ (12)

in contradiction to equation (4).

I have faith that equations (9,10) in textbooks are somehow correct, but because they look incorrect to me, I evidently have a misconception somewhere. I am trying to determine where and what that misconception is—Anita5192 (talk) 20:27, 25 November 2018 (UTC)

I do not know what you mean by equation (2) because you do not explain how you are using A. Equation (3) is obvious bull-shit. It should be

$x^{1}=3;x^{2}=4;x^{3}=12.$

Again I stopped reading at that point until you clean up your act. You must explain what all the variables in your equations mean or you will never get your head straight. JRSpriggs (talk) 01:58, 26 November 2018 (UTC)

I regret having mistaken the question. I thought to perceive a mix up of scalar coefficients and vectors, wherefore I dismissed the $x^{i}$s, seemingly used for both kinds, and introduced the $e_{i}$s for vectors and the $r^{i}$s for scalars, and wrote that boring triviality. Maybe, I tripped over the possibility of having abstract indices to denote vectors, but again, I have no formal conception for these. Purgy (talk) 07:08, 26 November 2018 (UTC)

I think I see where some of my misconceptions were. Correct me if I am wrong. (By chance, I discovered something in one of my books that clued me in, although it was not obvious.) Most textbooks that I have seen for linear algebra and tensors do not make clear the distinction between basis vectors, coordinate vectors, coordinates, and components. I tend to agree with Granzer92 (talk) in the previous section, that the Introduction did not make this clear either, and still does not. I have edited my original post above. Now equations (4) and (8) seem to agree with equations (9) and (10). Please let me know if I have this correct now.–Anita5192 (talk) 22:56, 27 November 2018 (UTC)

I agree to the reservations addressed by Granzer92, and admit not being a jour with JRSpriggs improvements. To my impression, much of this potential of confusion is caused by the wide spread, convenient notation of a basis-transformation, involving -say- "v-vectors" with bases-vectors as coordinates, and matrices of scalars as linear maps, without (sufficiently) emphasizing that the "v-vectors" live in "another" space than the basis-vectors, and that these spaces just share their scalars. The didactic migration from coordinate-bound to coordinate-free has not fully matured, yet, imho. Purgy (talk) 08:49, 28 November 2018 (UTC)

References

Notation burdened with crap.

Definition section would benefit hugely from being written with some sort of coherent standard of notation. I think we are probably allowed to assume that the reader knows what a linear transformation, basis, and coordinate vector with respect to a basis are, or certainly is capable of clicking links. There's no need to be summing over indices in both superscripts and subscripts and what the hell is this needless reference to the basis in brackets doing anyway? — Preceding unsigned comment added by 50.141.31.25 (talk) 21:47, 19 November 2015 (UTC)

1. I don't see any place the notation is incoherent. The components of a vector depend on the choice of basis, and the notation indicates clearly shows the basis. This dependence is appropriately emphasized throughout the section ("coherently"). In fact, I would say that the whole definition section is scrupulously coherent. A transformation of the basis is also shown clearly in the notation, and it is easy to show how this changes the vector and covector. Another way to indicate this dependence is using parentheses as opposed to square brackets (see, for example, Raymond Wells, Differential analysis on complex manifolds), with subscripts (e.g., Kobayashi and Nomizu, Foundations of differential geometry), or just with some ad hoc method (like "Let $v^{i}$ be the components of v in the basis f, and ${\tilde {v}}^{i}$ be the components of v in the basis ${\tilde {\mathbf {f} }}$"). It seems here better to use a notation where the dependence on the basis is explicitly emphasized, because that's what the article is really about.

2. "I think we are probably allowed to assume that the reader knows what a linear transformation, basis, and coordinate vector with respect to a basis are, or certainly is capable of clicking links." I agree with this, which is why the article doesn't define these things, except to write them down and fix the notation as it's used in the article, which is just a best practice for writing clear mathematics and not intended to be a substitute for knowledge that can be gleaned from clicking links. Also, linear transformations are not even mentioned until the very last section of the article. And the article doesn't define those either.

3. As for why the Einstein summation convention is not used in the definition section, it seems likely that some readers of the article will not have seen it before. It does no harm to include the summation sign. It's not like we are going to run out of ink, or expressions are going to become tangled messes of indices there. Covariance and contravariance should arguably be understood before the Einstein summation convention anyway, so presenting the additional of abstraction doesn't seem like there is any clear benefit to readers. Sławomir
Biały 22:41, 19 November 2015 (UTC)

It might be beneficial to change notation to such that vectors are bold-face lower-case letter, transformations are bold-face capital letters, while standard italics are used for scalars only. This convention is widespread in continuum mechanics, and, I believe, used in most elementary undergraduate courses. 130.209.157.54 (talk) 13:22, 14 January 2019 (UTC)

Introduction for the layman

I would add a paragraph to the introduction, which is easier to understand. Maybe something like this:

contravariant vectors

Let's say we have three base vectors a, b and c. Each one has the length 1 meter. d = (3,2,4) is a vector (≙ (3m,2m,4m)).If we now double the length of every base vector, so that |a| = |b| = |c| = 2m, then d must be (1.5, 1, 2) using the new a, b, c basis.(but d would still be (3m,2m,4m))

covariant vectors

Let's say f is a scalar function and the base of the coordinate system is a, b and c. And suppose |a| = |b| = |c| = 1 meter. Then suppose that ∇f=(2,5,9); so that the slope in x-direction is 2/ meter (2 per meter). If we now double the length of each base vector, so that |a| = |b| = |c| = 2m, ∇f becomes (4,10,18). The slope in x-direction is the same: 4/2m = 2/m.

CaffeineWitcher (talk) 12:59, 23 May 2020 (UTC)