Number, approximately 2.20557
Supersilver ratio A supersilver rectangle contains two scaled copies of itself, ς = ((ς − 1)2 + 2(ς − 1) + 1) / ς
Rationality irrational algebraic Symbol ς Decimal 2.2055694304 00590 31170 20286 ... Algebraic form real root of x 3 = 2x 2 + 1 Continued fraction (linear) [2;4,1,6,2,1,1,1,1,1,1,2,2,1,2,1,...]
In mathematics, the supersilver ratio is a geometrical proportion close to 75/34 . Its true value is the real solution of the equation x 3 = 2x 2 + 1.
The name supersilver ratio results from analogy with the silver ratio , the positive solution of the equation x 2 = 2x + 1supergolden ratio .
Two quantities a > b > 0 are in the supersilver ratio-squared if
(
2
a
+
b
a
)
2
=
a
b
{\displaystyle \left({\frac {2a+b}{a}}\right)^{2}={\frac {a}{b}}}
The ratio
2
a
+
b
a
{\displaystyle {\frac {2a+b}{a}}}
ς
.
{\displaystyle \varsigma .}
Based on this definition, one has
1
=
(
2
a
+
b
a
)
2
b
a
=
(
2
a
+
b
a
)
2
(
2
a
+
b
a
−
2
)
⟹
ς
2
(
ς
−
2
)
=
1
{\displaystyle {\begin{aligned}1&=\left({\frac {2a+b}{a}}\right)^{2}{\frac {b}{a}}\\&=\left({\frac {2a+b}{a}}\right)^{2}\left({\frac {2a+b}{a}}-2\right)\\&\implies \varsigma ^{2}\left(\varsigma -2\right)=1\end{aligned}}}
It follows that the supersilver ratio is found as the unique real solution of the cubic equation
ς
3
−
2
ς
2
−
1
=
0.
{\displaystyle \varsigma ^{3}-2\varsigma ^{2}-1=0.}
root begins as
2.205
569
430
400
590...
{\displaystyle 2.205\,569\,430\,400\,590...}
A356035 OEIS ).
The minimal polynomial for the reciprocal root is the depressed cubic
x
3
+
2
x
−
1
,
{\displaystyle x^{3}+2x-1,}
Cardano's formula ,
w
1
,
2
=
(
1
±
1
3
59
3
)
/
2
{\displaystyle w_{1,2}=\left(1\pm {\frac {1}{3}}{\sqrt {\frac {59}{3}}}\right)/2}
1
/
ς
=
w
1
3
+
w
2
3
{\displaystyle 1/\varsigma ={\sqrt[{3}]{w_{1}}}+{\sqrt[{3}]{w_{2}}}}
or, using the hyperbolic sine ,
1
/
ς
=
−
2
2
3
sinh
(
1
3
arsinh
(
−
3
4
3
2
)
)
.
{\displaystyle 1/\varsigma =-2{\sqrt {\frac {2}{3}}}\sinh \left({\frac {1}{3}}\operatorname {arsinh} \left(-{\frac {3}{4}}{\sqrt {\frac {3}{2}}}\right)\right).}
1
/
ς
{\displaystyle 1/\varsigma }
is the superstable fixed point of the iteration
x
←
(
2
x
3
+
1
)
/
(
3
x
2
+
2
)
.
{\displaystyle x\gets (2x^{3}+1)/(3x^{2}+2).}
Rewrite the minimal polynomial as
(
x
2
+
1
)
2
=
1
+
x
{\displaystyle (x^{2}+1)^{2}=1+x}
x
←
−
1
+
1
+
x
{\displaystyle x\gets {\sqrt {-1+{\sqrt {1+x}}}}}
continued radical
1
/
ς
=
−
1
+
1
+
−
1
+
1
+
⋯
{\displaystyle 1/\varsigma ={\sqrt {-1+{\sqrt {1+{\sqrt {-1+{\sqrt {1+\cdots }}}}}}}}\;}
[ 1] Dividing the defining trinomial
x
3
−
2
x
2
−
1
{\displaystyle x^{3}-2x^{2}-1}
x
−
ς
{\displaystyle x-\varsigma }
one obtains
x
2
+
x
/
ς
2
+
1
/
ς
{\displaystyle x^{2}+x/\varsigma ^{2}+1/\varsigma }
conjugate elements of
ς
{\displaystyle \varsigma }
are
x
1
,
2
=
(
−
1
±
i
8
ς
2
+
3
)
/
2
ς
2
,
{\displaystyle x_{1,2}=\left(-1\pm i{\sqrt {8\varsigma ^{2}+3}}\right)/2\varsigma ^{2},}
with
x
1
+
x
2
=
2
−
ς
{\displaystyle x_{1}+x_{2}=2-\varsigma \;}
x
1
x
2
=
1
/
ς
.
{\displaystyle \;x_{1}x_{2}=1/\varsigma .}
Rectangles with aspect ratios related to powers of ς The growth rate of the average value of the n-th term of a random Fibonacci sequence is
ς
−
1
{\displaystyle \varsigma -1}
.[ 2]
The supersilver ratio can be expressed in terms of itself as the infinite geometric series
ς
=
2
∑
k
=
0
∞
ς
−
3
k
{\displaystyle \varsigma =2\sum _{k=0}^{\infty }\varsigma ^{-3k}}
ς
2
=
−
1
+
∑
k
=
0
∞
(
ς
−
1
)
−
k
,
{\displaystyle \,\varsigma ^{2}=-1+\sum _{k=0}^{\infty }(\varsigma -1)^{-k},}
in comparison to the silver ratio identities
σ
=
2
∑
k
=
0
∞
σ
−
2
k
{\displaystyle \sigma =2\sum _{k=0}^{\infty }\sigma ^{-2k}}
σ
2
=
−
1
+
2
∑
k
=
0
∞
(
σ
−
1
)
−
k
.
{\displaystyle \,\sigma ^{2}=-1+2\sum _{k=0}^{\infty }(\sigma -1)^{-k}.}
For every integer
n
{\displaystyle n}
ς
n
=
2
ς
n
−
1
+
ς
n
−
3
=
4
ς
n
−
2
+
ς
n
−
3
+
2
ς
n
−
4
=
ς
n
−
1
+
2
ς
n
−
2
+
ς
n
−
3
+
ς
n
−
4
.
{\displaystyle {\begin{aligned}\varsigma ^{n}&=2\varsigma ^{n-1}+\varsigma ^{n-3}\\&=4\varsigma ^{n-2}+\varsigma ^{n-3}+2\varsigma ^{n-4}\\&=\varsigma ^{n-1}+2\varsigma ^{n-2}+\varsigma ^{n-3}+\varsigma ^{n-4}.\end{aligned}}}
Continued fraction pattern of a few low powers
ς
−
2
=
[
0
;
4
,
1
,
6
,
2
,
1
,
1
,
1
,
1
,
1
,
1
,
.
.
.
]
≈
0.2056
{\displaystyle \varsigma ^{-2}=[0;4,1,6,2,1,1,1,1,1,1,...]\approx 0.2056}
5/24 )
ς
−
1
=
[
0
;
2
,
4
,
1
,
6
,
2
,
1
,
1
,
1
,
1
,
1
,
.
.
.
]
≈
0.4534
{\displaystyle \varsigma ^{-1}=[0;2,4,1,6,2,1,1,1,1,1,...]\approx 0.4534}
5/11 )
ς
0
=
[
1
]
{\displaystyle \ \varsigma ^{0}=[1]}
ς
1
=
[
2
;
4
,
1
,
6
,
2
,
1
,
1
,
1
,
1
,
1
,
1
,
.
.
.
]
≈
2.2056
{\displaystyle \varsigma ^{1}=[2;4,1,6,2,1,1,1,1,1,1,...]\approx 2.2056}
53/24 )
ς
2
=
[
4
;
1
,
6
,
2
,
1
,
1
,
1
,
1
,
1
,
1
,
2
,
.
.
.
]
≈
4.8645
{\displaystyle \varsigma ^{2}=[4;1,6,2,1,1,1,1,1,1,2,...]\approx 4.8645}
73/15 )
ς
3
=
[
10
;
1
,
2
,
1
,
2
,
4
,
4
,
2
,
2
,
6
,
2
,
.
.
.
]
≈
10.729
{\displaystyle \varsigma ^{3}=[10;1,2,1,2,4,4,2,2,6,2,...]\approx 10.729}
118/11 )The supersilver ratio is a Pisot number .[ 3] absolute value
1
/
ς
{\displaystyle 1/{\sqrt {\varsigma }}}
ς
{\displaystyle \varsigma }
generate almost integers . For example:
ς
10
=
2724.00146856...
≈
2724
+
1
/
681.
{\displaystyle \varsigma ^{10}=2724.00146856...\approx 2724+1/681.}
phases of the inward spiraling conjugate pair – initially close to
±
45
π
/
82
{\displaystyle \pm 45\pi /82}
– nearly align with the imaginary axis.
The minimal polynomial of the supersilver ratio
m
(
x
)
=
x
3
−
2
x
2
−
1
{\displaystyle m(x)=x^{3}-2x^{2}-1}
discriminant
Δ
=
−
59
{\displaystyle \Delta =-59}
(
x
−
21
)
2
(
x
−
19
)
(
mod
59
)
;
{\displaystyle (x-21)^{2}(x-19){\pmod {59}};\;}
quadratic field
K
=
Q
(
Δ
)
{\displaystyle K=\mathbb {Q} ({\sqrt {\Delta }})}
class number
h
=
3.
{\displaystyle h=3.}
Thus, the Hilbert class field of
K
{\displaystyle K}
can be formed by adjoining
ς
.
{\displaystyle \varsigma .}
[ 4]
τ
=
(
1
+
Δ
)
/
2
{\displaystyle \tau =(1+{\sqrt {\Delta }})/2\,}
ring of integers of
K
{\displaystyle K}
, the real root j (τ )
(
ς
−
6
−
27
ς
6
−
6
)
3
.
{\displaystyle (\varsigma ^{-6}-27\varsigma ^{6}-6)^{3}.}
[ 5] [ 6]
The Weber-Ramanujan class invariant is approximated with error < 3.5 ∙ 10−20 by
2
f
(
Δ
)
=
2
4
G
59
≈
(
e
π
−
Δ
+
24
)
1
/
24
,
{\displaystyle {\sqrt {2}}\,{\mathfrak {f}}({\sqrt {\Delta }})={\sqrt[{4}]{2}}\,G_{59}\approx (e^{\pi {\sqrt {-\Delta }}}+24)^{1/24},}
while its true value is the single real root of the polynomial
W
59
(
x
)
=
x
9
−
4
x
8
+
4
x
7
−
2
x
6
+
4
x
5
−
8
x
4
+
4
x
3
−
8
x
2
+
16
x
−
8.
{\displaystyle W_{59}(x)=x^{9}-4x^{8}+4x^{7}-2x^{6}+4x^{5}-8x^{4}+4x^{3}-8x^{2}+16x-8.}
The elliptic integral singular value [ 7]
k
r
=
λ
∗
(
r
)
{\displaystyle k_{r}=\lambda ^{*}(r)}
r
=
59
{\displaystyle r=59}
has closed form expression
λ
∗
(
59
)
=
sin
(
arcsin
(
G
59
−
12
)
/
2
)
{\displaystyle \lambda ^{*}(59)=\sin(\arcsin \left(G_{59}^{-12}\right)/2)}
(which is less than 1/294 the eccentricity of the orbit of Venus).
Third-order Pell sequences [ edit ]
Hop o' my Thumb : a supersilver Rauzy fractal of type a ↦ baa. The fractal boundary has box-counting dimension 1.22
A supersilver Rauzy fractal of type c ↦ bca, with areas in the ratios ς 2 + 1 : ς (ς − 1) : ς : 1.
These numbers are related to the supersilver ratio as the Pell numbers and Pell-Lucas numbers are to the silver ratio .
The fundamental sequence is defined by the third-order recurrence relation
S
n
=
2
S
n
−
1
+
S
n
−
3
{\displaystyle S_{n}=2S_{n-1}+S_{n-3}}
n > 2with initial values
S
0
=
1
,
S
1
=
2
,
S
2
=
4.
{\displaystyle S_{0}=1,S_{1}=2,S_{2}=4.}
The first few terms are 1, 2, 4, 9, 20, 44, 97, 214, 472, 1041, 2296, 5064,... (sequence A008998 OEIS ).
The limit ratio between consecutive terms is the supersilver ratio.
The first 8 indices n for which
S
n
{\displaystyle S_{n}}
The sequence can be extended to negative indices using
S
n
=
S
n
+
3
−
2
S
n
+
2
{\displaystyle S_{n}=S_{n+3}-2S_{n+2}}
The generating function of the sequence is given by
1
1
−
2
x
−
x
3
=
∑
n
=
0
∞
S
n
x
n
{\displaystyle {\frac {1}{1-2x-x^{3}}}=\sum _{n=0}^{\infty }S_{n}x^{n}}
x
<
1
/
ς
.
{\displaystyle x<1/\varsigma \;.}
[ 8] The third-order Pell numbers are related to sums of binomial coefficients by
S
n
=
∑
k
=
0
⌊
n
/
3
⌋
(
n
−
2
k
k
)
⋅
2
n
−
3
k
{\displaystyle S_{n}=\sum _{k=0}^{\lfloor n/3\rfloor }{n-2k \choose k}\cdot 2^{n-3k}\;}
[ 9] The characteristic equation of the recurrence is
x
3
−
2
x
2
−
1
=
0.
{\displaystyle x^{3}-2x^{2}-1=0.}
α
{\displaystyle \alpha }
and conjugate pair
β
{\displaystyle \beta }
and
γ
{\displaystyle \gamma }
, the supersilver numbers can be computed with the Binet formula
S
n
−
2
=
a
α
n
+
b
β
n
+
c
γ
n
,
{\displaystyle S_{n-2}=a\alpha ^{n}+b\beta ^{n}+c\gamma ^{n},}
a
{\displaystyle a}
and conjugates
b
{\displaystyle b}
and
c
{\displaystyle c}
the roots of
59
x
3
+
4
x
−
1
=
0.
{\displaystyle 59x^{3}+4x-1=0.}
Since
|
b
β
n
+
c
γ
n
|
<
1
/
α
n
{\displaystyle \left\vert b\beta ^{n}+c\gamma ^{n}\right\vert <1/{\sqrt {\alpha ^{n}}}}
α
=
ς
,
{\displaystyle \alpha =\varsigma ,}
S
n
{\displaystyle S_{n}}
is the nearest integer to
a
ς
n
+
2
,
{\displaystyle a\,\varsigma ^{n+2},}
n ≥ 0
a
=
ς
/
(
2
ς
2
+
3
)
=
{\displaystyle a=\varsigma /(2\varsigma ^{2}+3)=}
0.1732702315 50408 18074 84794...
Coefficients
a
=
b
=
c
=
1
{\displaystyle a=b=c=1}
A
n
=
S
n
+
2
S
n
−
3
.
{\displaystyle A_{n}=S_{n}+2S_{n-3}.}
The first few terms are 3, 2, 4, 11, 24, 52, 115, 254, 560, 1235, 2724, 6008,... (sequence A332647 OEIS ).
This third-order Pell-Lucas sequence has the Fermat property : if p is prime,
A
p
≡
A
1
mod
p
.
{\displaystyle A_{p}\equiv A_{1}{\bmod {p}}.}
pseudoprimes
n
∣
(
A
n
−
2
)
{\displaystyle \,n\mid (A_{n}-2)}
108 to pass the test are n = 32 , 52 , 53 , 315, 99297, 222443, 418625, 9122185, 32572 , 11889745, 20909625, 24299681, 64036831, 76917325.[ 10]
The Pilgrim : a supersilver Rauzy fractal of type a ↦ aba. The three subtiles have areas in ratio ς.The third-order Pell numbers are obtained as integral powers n > 3matrix with real eigenvalue
ς
{\displaystyle \varsigma }
Q
=
(
2
0
1
1
0
0
0
1
0
)
,
{\displaystyle Q={\begin{pmatrix}2&0&1\\1&0&0\\0&1&0\end{pmatrix}},}
Q
n
=
(
S
n
S
n
−
2
S
n
−
1
S
n
−
1
S
n
−
3
S
n
−
2
S
n
−
2
S
n
−
4
S
n
−
3
)
{\displaystyle Q^{n}={\begin{pmatrix}S_{n}&S_{n-2}&S_{n-1}\\S_{n-1}&S_{n-3}&S_{n-2}\\S_{n-2}&S_{n-4}&S_{n-3}\end{pmatrix}}}
The trace of
Q
n
{\displaystyle Q^{n}}
gives the above
A
n
.
{\displaystyle A_{n}.}
Alternatively,
Q
{\displaystyle Q}
can be interpreted as incidence matrix for a D0L Lindenmayer system on the alphabet
{
a
,
b
,
c
}
{\displaystyle \{a,b,c\}}
with corresponding substitution rule
{
a
↦
a
a
b
b
↦
c
c
↦
a
{\displaystyle {\begin{cases}a\;\mapsto \;aab\\b\;\mapsto \;c\\c\;\mapsto \;a\end{cases}}}
and initiator
w
0
=
b
{\displaystyle w_{0}=b}
. The series of words
w
n
{\displaystyle w_{n}}
produced by iterating the substitution have the property that the number of c's, b's and a's are equal to successive third-order Pell numbers. The lengths of these words are given by
l
(
w
n
)
=
S
n
−
2
+
S
n
−
3
+
S
n
−
4
.
{\displaystyle l(w_{n})=S_{n-2}+S_{n-3}+S_{n-4}.}
[ 11]
Associated to this string rewriting process is a compact set composed of self-similar tiles called the Rauzy fractal , that visualizes the combinatorial information contained in a multiple-generation three-letter sequence.[ 12]
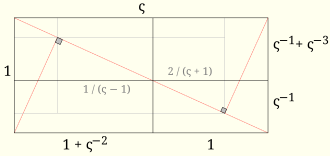
Supersilver rectangle [ edit ] Powers of ς Given a rectangle of height 1 , length
ς
{\displaystyle \varsigma }
and diagonal length
ς
ς
−
1
.
{\displaystyle \varsigma {\sqrt {\varsigma -1}}.}
altitudes
1
/
ς
−
1
;
{\displaystyle 1/{\sqrt {\varsigma -1}}\,;}
ς
2
{\displaystyle \varsigma ^{2}}
.
On the right-hand side, cut off a square of side length 1 and mark the intersection with the falling diagonal. The remaining rectangle now has aspect ratio
1
+
1
/
ς
2
:
1
{\displaystyle 1+1/\varsigma ^{2}:1}
ς
=
2
+
1
/
ς
2
{\displaystyle \varsigma =2+1/\varsigma ^{2}}
[ 13]
The parent supersilver rectangle and the two scaled copies along the diagonal have linear sizes in the ratios
ς
:
ς
−
1
:
1.
{\displaystyle \varsigma :\varsigma -1:1.}
(
ς
−
1
)
/
ς
,
{\displaystyle (\varsigma -1)/\varsigma ,}
ς
(
ς
−
1
)
{\displaystyle \varsigma (\varsigma -1)}
ς
/
(
ς
−
1
)
{\displaystyle \varsigma /(\varsigma -1)}
If the diagram is further subdivided by perpendicular lines through the feet of the altitudes, the lengths of the diagonal and its seven distinct subsections are in ratios
ς
2
+
1
:
ς
2
:
ς
2
−
1
:
ς
+
1
:
{\displaystyle \varsigma ^{2}+1:\varsigma ^{2}:\varsigma ^{2}-1:\varsigma +1:}
ς
(
ς
−
1
)
:
ς
:
2
/
(
ς
−
1
)
:
1.
{\displaystyle \,\varsigma (\varsigma -1):\varsigma :2/(\varsigma -1):1.}
Solutions of equations similar to
x
3
=
2
x
2
+
1
{\displaystyle x^{3}=2x^{2}+1}
Silver ratio – the only positive solution of the equation
x
2
=
2
x
+
1
{\displaystyle x^{2}=2x+1}
Golden ratio – the only positive solution of the equation
x
2
=
x
+
1
{\displaystyle x^{2}=x+1}
Supergolden ratio – the only real solution of the equation
x
3
=
x
2
+
1
{\displaystyle x^{3}=x^{2}+1}
^ Sloane, N. J. A. (ed.). "Sequence A272874" . The On-Line Encyclopedia of Integer Sequences . OEIS Foundation.^ (sequence A137421 OEIS )
^ Panju, Maysum (2011). "A systematic construction of almost integers" (PDF) . The Waterloo Mathematics Review . 1 (2): 35–43. ^ "Hilbert class field of a quadratic field whose class number is 3" . Mathematics stack exchange . 2012. Retrieved May 1, 2024 .^ Berndt, Bruce C.; Chan, Heng Huat (1999). "Ramanujan and the modular j-invariant" . Canadian Mathematical Bulletin 42 (4): 427–440. doi :10.4153/CMB-1999-050-1 ^ Johansson, Fredrik (2021). "Modular j-invariant" . Fungrim . Retrieved April 30, 2024 . Table of Hilbert class polynomials ^ Weisstein, Eric W. "Elliptic integral singular value" . MathWorld ^ (sequence A008998 OEIS )
^ Mahon, Br. J. M.; Horadam, A. F. (1990). "Third-order diagonal functions of Pell polynomials". The Fibonacci Quarterly 28 (1): 3–10. doi :10.1080/00150517.1990.12429513 . ^ Only one of these is a 'restricted pseudoprime' as defined in: Adams, William; Shanks, Daniel (1982). "Strong primality tests that are not sufficient" . Mathematics of Computation 39 (159). American Mathematical Society : 255–300. doi :10.1090/S0025-5718-1982-0658231-9 JSTOR 2007637 .
^ for n ≥ 2 (sequence A193641 OEIS )
^ Siegel, Anne; Thuswaldner, Jörg M. (2009). "Topological properties of Rauzy fractals" . Mémoires de la Société Mathématique de France . 2. 118 : 1–140. doi :10.24033/msmf.430 . ^ Analogue to the construction in: Crilly, Tony (1994). "A supergolden rectangle". The Mathematical Gazette 78 (483): 320–325. doi :10.2307/3620208 . JSTOR 3620208 .














![{\displaystyle 1/\varsigma ={\sqrt[{3}]{w_{1}}}+{\sqrt[{3}]{w_{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa28739bc37d917473d0a0b1e36de751b58b6b6c)




















![{\displaystyle \varsigma ^{-2}=[0;4,1,6,2,1,1,1,1,1,1,...]\approx 0.2056}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea6063fd9c917e986eff40e95be1f667e087e58b)
![{\displaystyle \varsigma ^{-1}=[0;2,4,1,6,2,1,1,1,1,1,...]\approx 0.4534}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e5f44e0e9486d2fabf97ecf739992bfe432316b)
![{\displaystyle \ \varsigma ^{0}=[1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8f53f05487590d1d73db17aae5b6171d9dcbba3)
![{\displaystyle \varsigma ^{1}=[2;4,1,6,2,1,1,1,1,1,1,...]\approx 2.2056}](https://wikimedia.org/api/rest_v1/media/math/render/svg/16fbcc3cc1776b6cb1af32abb7b492a0d3720d0a)
![{\displaystyle \varsigma ^{2}=[4;1,6,2,1,1,1,1,1,1,2,...]\approx 4.8645}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f43eeb5bc0b1911a450c2b8b91e056ddc1e8aba)
![{\displaystyle \varsigma ^{3}=[10;1,2,1,2,4,4,2,2,6,2,...]\approx 10.729}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9456843303f4a5d95793ec238dccc3c05131386)











![{\displaystyle {\sqrt {2}}\,{\mathfrak {f}}({\sqrt {\Delta }})={\sqrt[{4}]{2}}\,G_{59}\approx (e^{\pi {\sqrt {-\Delta }}}+24)^{1/24},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd8132fde5fa9086fa21ae8705c991382212ace3)




















































