Shape of the atomic nucleus

The shape of the atomic nucleus depends on the variety of factors related to the size and shape of its nucleon constituents and the nuclear force holding them together. The origins of nuclear shape begin with the spacial extent (aka root mean squared charge radius) of almost nearly all stable and a great many unstable nuclei has been determined mainly by electron and muon scattering experiments as well as spectroscopic experiments.[2] An important factor in the internal structure of the nucleus is the nucleon-nucleon potential, which ultimately governs the distance between individual nucleons,[3] while a dip in the charge density of some light nuclide structures a lesser density of nucleonic matter.[4] A surprising non-spherical expectation for the shape of the nucleus originated in 1939 in the spectroscopic analysis of the quadrupole moments[5] while the prolate spheroid shape of the nucleon arises from analysis of the intrinsic quadruple moment.[1] The simple spherical approximation of nuclear size and shape provides at best a textbook introduction to nuclear size and shape.[6] The unusual cosmic abundance of alpha nuclides has inspired geometric arrangements of alpha particles as a solution to nuclear shapes, although the atomic nucleus generally assumes a prolate spheroid shape. Nuclides can also be discus-shaped (oblate deformation), triaxial (a combination of oblate and prolate deformation) or pear-shaped.[7][8]
Origins of nuclear shape
[edit]The atomic nucleus is composed of protons and neutrons (collectively called nucleons). In the Standard model of particle physics, nucleons are in the group called hadrons, the smallest known particles in the universe to have measurable size and shape.[1] Each is in turn composed of three quarks. The spatial extent and shape of nucleons (and nuclides assembled from them) ultimately involves quark interactions within and between nucleons. The quark itself does not have measurable size at the experimental limit set by the electron (≈ 10−18 m in diameter).[9] The size, or root mean squared (RMS) charge radius, of the proton (the smallest nuclide) has a 2018 CODATA recommended value of 0.8414 (19) fm (10−15 m), although values may vary by a few percent according to the experimental method employed (see proton radius puzzle). Nuclide size ranges up to ≈ 6 fm. The largest stable nuclide, lead-208, has an RMS charge radius of 5.5012 fm, and the largest unstable nuclide americium-243 has an experimental RMS charge radius of 5.9048 fm.[2] The main source of nuclear radius values derives from elastic scattering experiments (electron and muon), but nuclear radii data also come from experiments on spectroscopic isotope shifts (x-ray and optical), β decay by mirror nuclei, α decay, and neutron scattering.[10] Although the radius values delimit the spatial extent of the nucleus, spectroscopic and scattering experiments dating back to 1935[11] in many cases indicate a deviation of the nuclear charge distribution or quadrupole moment consistent with non-spherical nuclear shapes for many nuclei.
Simple spherical approximation
[edit]
The atomic nucleus been depicted as a compact bundle of the two types of nucleons depicted as hard-packed spheres. This depiction of the atomic nucleus only approximates the empirical evidence for the size and shape of the nucleus. The root mean squared (RMS) charge radius of most stable (and many unstable) nuclides have been experimentally determined.[2] If the nucleus is assumed to be spherically symmetric, an approximate relationship between nuclear radius and mass number arises above A=40 from the formula R=RoA1/3 with Ro = 1.2 ± 0.2 fm.[6] R is the predicted spherical nuclear radius, A is the mass number, and Ro is a constant determined by experimental data. This radius to mass relationship has its roots in the liquid drop model as proposed by Gamow in 1930.[12] The graph on the right plots the radius-to-mass of the experimental charge radius (blue line)[2] as compared to the spherical approximation (green line). For light nuclides below A=40, the smooth curvilinear spherical radius plot contrasts with the erratic experimental radius-to-mass. For medium and heavy nuclides above A=40, the plots converge and run approximately parallel when Ro = 1.
Nucleon shape
[edit]The empirical knowledge of nucleon shape originates from the study of the transition from the proton ground state N(938) to the first excited state ∆+(1232).[1] Multiple studies using a variety of models have led to an expectation of non-spherical shape. The proton's RMS charge radius of 0.8414 fm only defines the spatial extent of its charge distribution, i.e. the distance from its center of mass to its farthest point. Examination of the angular dependence of the charge distribution indicates that the proton is not a perfect sphere. Model-dependent analyses of the intrinsic quadrupole moment suggests that the ground-state nucleon shape conforms to a prolate spheroid shape.[13]
The intrinsic quadrupole moment is distinct from the spectroscopic quadrupole moment, as realized more than 50 years ago.[14] The intrinsic quadrupole moment relates to a body-fixed coordinate system that rotates with the nucleon in contrast to the spectroscopically measured quadrupole moment. While the nucleon's spectroscopic quadrupole moment is zero due to angular moment selection rules related to spin, the non-zero intrinsic quadrupole is obtained by electromagnetic quadrupole transitions between the nucleon ground N(938) and ∆(1232) excited states.[15] The proton and neutron have nearly the same mass (938 MeV),[16] and may be regarded as one particle, the nucleon N(938),with two different charge states (proton +1, and neutron 0).[17] The proton's N(938) ground state and ∆+(1232) excited state have different shapes.[18] The transition between the states supports a prolate spheroid deformation for the ground state, and an oblate spheroid deformation for the excited state.

The prolate shaped ground state reflects quark-to-quark interactions arising from the Pauli exclusion principle. In the ground state, the two down quarks of a ground-state neutron are in an isospin 1 state, and simultaneously in a spin 1 state in order that the spin-isospin wave function is symmetric.[17] The exclusion principle is built into the anti-symmetric fermionic wave function, thereby forbidding a pair of identical fermions from occupying the same quantum state.[19] In accordance with Pauli exclusion force,[dubious – discuss] the spin-spin repulsive force between identical fermions pushes like-flavored quarks further apart. Conversely, when the spins of a pair of unlike fermions align, such as an up-/down-quark pair within a ground-state nucleon, the nuclear force is attractive and draws the particles close to other each other without violating the Pauli exclusion principle.[15] Within the ground state neutron, this results in a picture of the spin interactions (above) in which the two down quarks (like fermions) qualitatively repel to either end of the prolate nucleon structure while simultaneously attracting to the up quark (unlike fermion) in the middle. Similar spin-spin interactions play out in the proton, considered identical to the neutron but existing in a different charge state.[19]
Electron scattering techniques pioneered by Robert Hofstadter gave the first indication of a deeper structure for the nucleon.[20] The technique is similar in principle to Rutherford's gold foil experiment in which alpha particles are directed at a thin gold foil, but Hofstadter's use of electrons, rather than alpha particles, enabled much higher resolution. The radial charge density of the neutron in particular was shown to have a complex internal structure consisting of a positive core and a negative skin, qualitatively consistent with the neutron's quark charge distribution shown above.[20][21][22] Hofstadter received a Nobel prize for this work in 1961, several years before Murray Gell-Mann posited the quark model in 1965.[21]
Space between nucleons
[edit]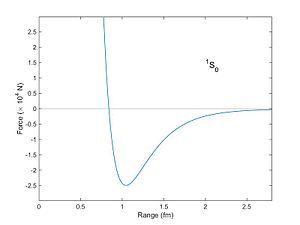
The atomic nucleus is a bound system of protons and neutrons. The spatial extent and shape of the nucleus depend not only on the size and shape of discrete nucleons, but also on the distance between them (the inter-nucleon distance). (Other factors include spin, alignment, orbital motion, and the local nuclear environment (see EMC effect).) The proximity of adjacent nucleons is governed by the nucleon-nucleon potential, and the force between a pair of nucleons can be obtained by taking the derivative of the potential. The strong nuclear force between nucleons is short-range, and the interaction between a pair of nucleons depends on the distance between them . Below 0.5 fm, each nucleon has a repulsive hard core that prevents neighboring nucleons from approaching any closer.[23] Repulsive and attractive forces balance at ≈ 0.8 fm, and become maximally attractive at ≈ 1.0 fm, as illustrated in the diagram.[3] Because energy is required to separate them, the pair of nucleons are said to be in a bound state. The proton-neutron (p-n) bound state, or p-n pair, is stable and ubiquitous in baryonic matter.[24] The p-n pair contributes implicitly to the top ten most abundant isotopes in the universe, eight of which contain equal numbers of protons and neutrons (see Oddo-Harkins rule and abundance of the elements). Conversely, the proton-proton (diproton) and neutron-neutron (dineutron) bound states are unstable and therefore rarely found in nature. The deuteron (the simplest p-n pair) does not have a spherical shape owing to its quadrupole moment.[5] The transverse charge density of the deuteron now confirms a prolate or elongated shape.[25]
Soft core of light nuclides
[edit]
Electron scattering techniques have yielded clues as to the internal structure of light nuclides. Proton-neutron pairs experience a strongly repulsive component of the nuclear force within ≈ 0.5 fm (see "Space between nucleons" above). As nucleons cannot pack any closer, nearly all nuclei have the same central density.[6] While this statement generally holds true for nuclides above calcium-40, electron scattering experiments of many of the lighter nuclides reveal a nuclear core that is remarkably less dense then the rest of the nucleus. Model-independent analyses of nuclear charge densities for both He-3 and He-4, for example, indicate a significant central depression within a radius of 0.8 fm.[4] Other light nuclides, including carbon-12 and oxygen-16, exhibit similar off-center charge density maxima.[20][26] A lower radial charge density within the nuclear core reflects a lower likelihood that scattering electrons will encounter a nucleon near the center of the nucleus compared to the surrounding nuclear structure.
Alpha particle as possible building block
[edit]
Although the proton and the neutron are the building blocks of the atomic nucleus, the unusual natural abundance of alpha nuclides has prompted investigations of the role of the alpha particle, or helium-4 nucleus, as a potential building block of matter.[27] Alpha cluster models envision the atomic nucleus as having discrete alpha particles that occupy average relative positions. Hydrogen makes up 74% of the ordinary baryonic matter of the universe, but 99% of the remaining matter is contained within just eight nuclides (, , , , , , , and ), seven of which are alpha nuclides. In the table below, the shapes of these nuclides may correspond to simple geometric arrangements of alpha particles, with associated radius predictions.[28]
| Nuclide | Number of α-particles |
Geometry[29] | Radius | |
|---|---|---|---|---|
| Predicted[28] | Experimental[2] | |||
| 3 | Triangle[30] | 2.43 fm | 2.47 fm | |
| 4 | Tetrahedron[31] | 2.54 fm | 2.70 fm | |
| 5 | Trigonal bipyramid | 2.76 fm | 3.01 fm | |
| Square pyramid | 2.79 fm | |||
| 6 | Octahedron | 2.85 fm | 3.06 fm | |
| Hexagon | 3.79 fm | |||
| 8 | Cubic | 3.37 fm | 3.26 fm | |
| Octagon | 4.85 fm | |||
Heavier nuclides
[edit]For many medium-to-heavy nuclides, in particular those far from the magic numbers of protons and neutrons, a spherical model of the atomic nucleus is incompatible with observed large quadrupole moments, indicating that lower potential energy is obtained for an ellipsoidal shape than for a spherical nucleus of the same volume.[32] In general, their ground states tend towards a prolate shape,[33] although experimental data hint at oblate ground-state shapes in certain nuclei, for example krypton-72.[34] Experiments also suggest that some heavy nuclei, such as barium-144 and radium-224, possess asymmetric pear shapes evidenced by their measured octupole moments.[35][36][37] It is also possible for a nucleus to adopt different shapes in states with a similar excitation energy, which is referred to as shape coexistence.[38] For example, the ground states of krypton-74 and krypton-76 have prolate shapes, but there is evidence for oblate-shape excited structures in these nuclei appearing at low excitation energy. In this particular case, the shapes of coexisting structures tend to mix together.[39]
References
[edit]- ^ a b c d Alexandrou C, Papanicolas CN, Vanderhaeghen M (2012-09-11). "Colloquium : The Shape of Hadrons". Reviews of Modern Physics. 84 (3): 1231–1251. Bibcode:2012RvMP...84.1231A. doi:10.1103/RevModPhys.84.1231. ISSN 0034-6861.
- ^ a b c d e Angeli I, Marinova KP (January 2013). "Table of experimental nuclear ground state charge radii: An update". Atomic Data and Nuclear Data Tables. 99 (1): 69–95. Bibcode:2013ADNDT..99...69A. doi:10.1016/j.adt.2011.12.006.
- ^ a b c Reid RV (December 1968). "Local phenomenological nucleon-nucleon potentials". Annals of Physics. 50 (3): 411–448. Bibcode:1968AnPhy..50..411R. doi:10.1016/0003-4916(68)90126-7. ISSN 0003-4916.
- ^ a b McCarthy JS, Sick I, Whitney RR (1977). "Electromagnetic structure of the helium isotopes". Phys. Rev. C. 15 (4): 1396–1414. Bibcode:1977PhRvC..15.1396M. doi:10.1103/PhysRevC.15.1396.
- ^ a b Kellogg JM, Rabi II, Ramsey Jr NF, Zacharias JR (1939). "An Electrical Quadrupole Moment of the Deuteron". Phys. Rev. 55 (318): 318–319. Bibcode:1939PhRv...55..318K. doi:10.1103/PhysRev.55.318.
- ^ a b c Tipler P, Llewellyn R (2012). "Chapter 11 - The Nuclear Force". Modern Physics (6th ed.). New York: W. H. Freeman and Company. ISBN 978-1-4641-1935-4.
- ^ Battersby S (2013). "Pear-shaped nucleus boosts search for new physics". Nature. doi:10.1038/nature.2013.12952. S2CID 124188454. Archived from the original on September 17, 2016. Retrieved November 23, 2017.
- ^ Gaffney, L. P., Butler, P A, Scheck, M, Hayes, A B, Wenander, F, Albers, M, et al. (2013). "Studies of pear-shaped nuclei using accelerated radioactive beams" (PDF). Nature. 497 (7448): 199–204. Bibcode:2013Natur.497..199G. doi:10.1038/nature12073. ISSN 0028-0836. PMID 23657348. S2CID 4380776. Archived (PDF) from the original on August 30, 2017. Retrieved September 13, 2016.
- ^ Gabrielse G, Hanneke D, Kinoshita T, Nio M, Odom B (July 2006). "New determination of the fine structure constant from the electron value and QED". Physical Review Letters. 97 (3): 030802. Bibcode:2006PhRvL..97c0802G. doi:10.1103/PhysRevLett.97.030802. PMID 16907491.
- ^ Gauthier N (April 1989). "Deriving a formula for nuclear radii using the measured atomic masses of elements". American Journal of Physics. 57 (4): 344–346. Bibcode:1989AmJPh..57..344G. doi:10.1119/1.16044. ISSN 0002-9505.
- ^ Brix B (1986). "On the shoulders of giants — Early history of hyperfine structure spectroscopy". Zeitschrift für Naturforschung B. 41. doi:10.1007/bfb0104339.
- ^ Gamow G (1930). "Mass Defect Curve and Nuclear Constitution". Proceedings of the Royal Society of London. 126 (803): 632–644. Bibcode:1930RSPSA.126..632G. doi:10.1098/rspa.1930.0032.
- ^ Bernstein AM (2003). "Deviation of the Nucleon Shape From Spherical Symmetry: Experimental Status". Eur. Phys. J. A. 17 (3): 349–355. arXiv:hep-ex/0212032. Bibcode:2003EPJA...17..349B. doi:10.1140/epja/i2002-10176-7.
- ^ Bohr A, Mottelson B (1975). Nuclear Structure II. Reading: A. Benjamin. ISBN 978-981-02-3979-4.
- ^ a b Buchmann AJ, Henley EM (2000). "Intrinsic quadrupole moment of the nucleon". Phys. Rev. C. 63 (1): 015202. arXiv:hep-ph/0101027. Bibcode:2000PhRvC..63a5202B. doi:10.1103/PhysRevC.63.015202.
- ^ Mohr PJ, Newell DB, Taylor BN (July–September 2016). "CODATA recommended values of the fundamental physical constants: 2014". Reviews of Modern Physics. 88 (3): 035009. arXiv:1507.07956. Bibcode:2016RvMP...88c5009M. doi:10.1103/RevModPhys.88.035009.
- ^ a b c Buchmann AJ (April 2005). "Nucleon deformation and atomic spectroscopy". Canadian Journal of Physics. 83 (4): 455–465. arXiv:physics/0508007. Bibcode:2005CaJPh..83..455B. doi:10.1139/p05-009. ISSN 0008-4204.
- ^ Tiator L, Drechsel D, Kamalov S, Yang S (2003). "Electromagnetic form factors of the ∆(1232) excitation". Eur. Phys. J. A. 17: 357–363. doi:10.1140/epja/i2002-10177-6.
- ^ a b Das A, Ferbel T (2003). Nuclear and Particle Physics. Hackensack, New Jersey, USA: World Scientific. ISBN 9789812387448.
- ^ a b c Hofstadter R (11 December 1961). "Nobel Lecture". Archived from the original on 28 January 2023. Retrieved 16 February 2023.
Figure 8
- ^ a b Littauer RM, Schopper HF, Wilson RR (1961). "Structure of the Proton and Neutron". Physical Review Letters. 7 (4): 144–147. Bibcode:1961PhRvL...7..144L. doi:10.1103/PhysRevLett.7.144.
- ^ Wietfeldt FE, Huber M, Black TC, Kaiser H, Arif M, Jacobson DL, et al. (November 2006). "Measuring the neutron's mean square charge radius using neutron interferometry". Physica B: Condensed Matter. 385: 1374–1376. arXiv:nucl-ex/0509018. Bibcode:2006PhyB..385.1374W. doi:10.1016/j.physb.2006.05.187. ISSN 0921-4526.
- ^ Bohr A, Mottelson BR (1998). Nuclear Structure. Vol. 1. Reading, MA: Benjamin. ISBN 978-981-02-3979-4.
- ^ Korover I, Denniston AW, Kiral A, Schmidt A, Lovato A, Rocco N, et al. (CLAS Collaboration) (2023-06-06). "Observation of large missing-momentum cross-section scaling and the onset of correlated-pair dominance in nuclei". Physical Review C. 107 (6): L061301. arXiv:2209.01492. doi:10.1103/PhysRevC.107.L061301.
- ^ Carlson CE, Vanderhaeghen M (July 2009). "Empirical transverse charge densities in the deuteron". The European Physical Journal A. 41 (1): 1–5. arXiv:0807.4537. Bibcode:2009EPJA...41....1C. doi:10.1140/epja/i2009-10800-0. ISSN 1434-601X.
- ^ a b Frois B (January 1985). "Electron scattering and nuclear structure". Progress in Particle and Nuclear Physics. 13: 117–148. Bibcode:1985PrPNP..13..117F. doi:10.1016/0146-6410(85)90005-5. ISSN 0146-6410.
- ^ Otsuka T, Abe T, Yoshida T, Tsunoda Y, Shimizu N, Itagaki N, et al. (April 2022). "α-Clustering in atomic nuclei from first principles with statistical learning and the Hoyle state character". Nature Communications. 13 (1): 2234. Bibcode:2022NatCo..13.2234O. doi:10.1038/s41467-022-29582-0. PMC 9046222. PMID 35477704.
- ^ a b Royer G, Eudes P (June 2017). "Alpha clustering and nuclear molecules in 8 Be, 12 C, 16 O, 20 Ne, 24 Mg, and 32 S". Journal of Physics: Conference Series. 863: 012012. doi:10.1088/1742-6596/863/1/012012. ISSN 1742-6588.
- ^ Royer G, Ramasamy G, Eudes P (2015-11-16). "Energies of molecular structures in 12 C, 16 O, 20 Ne, 24 Mg, and 32 S" (PDF). Physical Review C. 92 (5): 054308. doi:10.1103/PhysRevC.92.054308. Archived (PDF) from the original on 2023-12-28. Retrieved 2024-03-30.
- ^ Marín-Lámbarri DJ, Bijker R, Freer M, Gai M, Kokalova T, Parker DJ, et al. (July 2014). "Evidence for triangular D3h symmetry in 12C". Physical Review Letters. 113 (1): 012502. arXiv:1405.7445. Bibcode:2014PhRvL.113a2502M. doi:10.1103/PhysRevLett.113.012502. PMID 25032922.
- ^ Bijker R, Iachello F (April 2014). "Evidence for tetrahedral symmetry in (16)O". Physical Review Letters. 112 (15): 152501. arXiv:1403.6773. Bibcode:2014PhRvL.112o2501B. doi:10.1103/PhysRevLett.112.152501. PMID 24785032.
- ^ Rainwater J (August 1950). "Nuclear Energy Level Argument for a Spheroidal Nuclear Model". Physical Review. 79 (3): 432–434. Bibcode:1950PhRv...79..432R. doi:10.1103/PhysRev.79.432.
- ^ Tajima N, Suzuki N (2001-08-08). "Prolate dominance of nuclear shape caused by a strong interference between the effects of spin-orbit and ${l}^{2}$ terms of the Nilsson potential". Physical Review C. 64 (3): 037301. arXiv:nucl-th/0103061. doi:10.1103/PhysRevC.64.037301.
- ^ Bouchez E, Matea I, Korten W, Becker F, Blank B, Borcea C, et al. (February 2003). "New shape isomer in the self-conjugate nucleus 72Kr". Physical Review Letters. 90 (8): 082502. doi:10.1103/PhysRevLett.90.082502. PMID 12633421. Archived from the original on 2024-04-12. Retrieved 2024-03-30.
- ^ Bucher B, Zhu S, Wu CY, Janssens RV, Cline D, Hayes AB, et al. (March 2016). "Direct Evidence of Octupole Deformation in Neutron-Rich ^{144}Ba". Physical Review Letters. 116 (11): 112503. arXiv:1602.01485. doi:10.1103/PhysRevLett.116.112503. PMID 27035298.
- ^ Battersby S (2013-05-08). "Pear-shaped nucleus boosts search for new physics". Nature. doi:10.1038/nature.2013.12952. ISSN 1476-4687.
- ^ Butler PA (July 2020). "Pear-shaped atomic nuclei". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 476 (2239): 20200202. Bibcode:2020RSPSA.47600202B. doi:10.1098/rspa.2020.0202. PMC 7426035. PMID 32821242.
- ^ Wood JL, Heyde K (2011-11-30). "Shape coexistence in atomic nuclei". Reviews of Modern Physics. 83 (4): 1467–1521. doi:10.1103/RevModPhys.83.1467.
- ^ Clément E, Görgen A, Korten W, Bouchez E, Chatillon A, Delaroche JP, et al. (2007-05-10). "Shape coexistence in neutron-deficient krypton isotopes" (PDF). Physical Review C. 75 (5): 054313. Bibcode:2007PhRvC..75e4313C. doi:10.1103/PhysRevC.75.054313.








