List of irreducible Tits indices

In the mathematical theory of linear algebraic groups, a Tits index (or index) is an object used to classify semisimple algebraic groups defined over a base field k, not assumed to be algebraically closed. The possible irreducible indices were classified by Jacques Tits, and this classification is reproduced below. (Because every index is a direct sum of irreducible indices, classifying all indices amounts to classifying irreducible indices.)

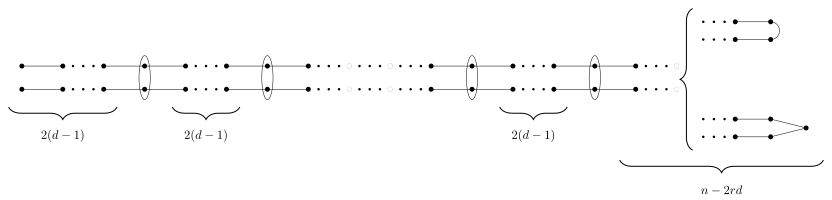
Organization of the list

An index can be represented as a Dynkin diagram with certain vertices drawn close to each other (the orbit of the vertices under the *-action of the Galois group of k) and with certain sets of vertices circled (the orbits of the non-distinguished vertices under the *-action). This representation captures the full information of the index except when the underlying Dynkin diagram is D₄, in which case one must distinguish between an action by the cyclic group C₃ or the permutation group S₃.

Alternatively, an index can be represented using the name of the underlying Dynkin diagram together with additional superscripts and subscripts, to be explained momentarily. This representation, together with the labeled Dynkin diagram described in the previous paragraph, captures the full information of the index.

The notation for an index is of the form ^gX^t
_n,r, where

• X is the letter of the underlying Dynkin diagram (A, B, C, D, E, F, or G),
• n is the number of vertices of the Dynkin diagram,
• r is the relative rank of the corresponding algebraic group,
• g is the order of the quotient of the absolute Galois group that acts faithfully on the Dynkin diagram (so g = 1, 2, 3, or 6), and
• t is either
  • the degree of a certain division algebra (that is, the square root of its dimension) arising in the construction of the algebraic group when the group is of classical type (A, B, C, or D), in which case t is written in parentheses, or
  • the dimension of the anisotropic kernel of the algebraic group when the group is of exceptional type (E, F, or G), in which case t is written without parentheses.

In the description, there are given (only for classical groups), a representative of the isogeny class of the group of the given Tits index.

The following complete list of all possible Tits indices over those special fields, which are the finite fields, the local and global fields (in any characteristic) is given (see and (with full proof)).

The related sources are, and.

A_n

¹A_n

Full name: ¹A^(d)
_n,r

Image:

Conditions: d · (r + 1) = n + 1, d ≥ 1.

Distinguished vertices: d, 2d,...,rd.

Description: Algebraic group: The special linear group SL_r+1(D) where D is a central division algebra over k.

Special fields: Over a finite field, d = 1; over the reals, d = 1 or 2; over a p-adic field or a number field, or any local or global function field, d is arbitrary.

²A_n

Full name: ²A^(d)
_n,r

Image:

Conditions: d | n + 1, d ≥ 1, 2rd ≤ n + 1.

Distinguished vertices: (d,n+1-d),(2d,n+1-2d),...,(rd,n+1-rd).

Description: Algebraic group: The special unitary group SU_(n+1)/d(D,h), where D is a central division algebra of degree d over a separable quadratic extension k' of k, and where h is a nondegenerate hermitian form of index r relative to the unique non-trivial k-automorphism of k' .

Special fields: Over a finite field, d = 1 and r = ⌊(n+1)/2⌋; over the reals, d = 1; over a p-adic field or local function field, d = 1 and n = 2r − 1, 2r, 2r+1. Over a real number field, d and r are arbitrary; over a totally imaginary number field, d=1 and n = 2r − 1, 2r, 2r+1, or d>1 and (n+1)/d-2r =0,1; over a global function field, d=1 and n = 2r, 2r+1, 2r+2, or d>1 and (n+1)/d-2r =0,1.

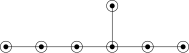
B_n

Full name: B_n,r

Image:

Conditions: None.

Distinguished vertices: 1, 2,...,r.

Description: Algebraic group: The special orthogonal group SO_2n+1(k,q), where q is a quadratic form of index r, and defect 1 if k has characteristic 2.

Special fields: Over a finite field, r = n; over a p-adic field or local function field, r = n or n − 1 (and if char.k=2, defect 1); over the reals or a real number field, r is arbitrary; over a totally imaginary number field or a global function field, r = n or n − 1 (and if char.k=2, defect 1).

C_n

Full name: C^(d)
_n,r

Image:

Conditions: d = 2^a | 2n, d ≥ 1; n = r if d = 1.

Distinguished vertices: d, 2d,...,rd.

Description: Algebraic group: The special unitary group SU_2n/d(D,h), where D is a division algebra of degree d over k and h is a nondegenerate antihermitian form relative to a k-linear involution σ of D (also called an "involution of the first kind") such that the fixed-point subring D^σ has dimension d(d + 1)/2; or equivalently, when d > 1 and char k ≠ 2, the group SU_2n/d where D and h are as above except that h is hermitian and D has dimension d(d − 1)/2. When d = 1, this group is the symplectic group Sp_2n(k).

Special fields: Over a finite field, d = 1; over the reals or a real number field, d = 1 (and r = n) or d = 2; over a p-adic field, local function field, totally imaginary number field or global function field, d = 1 (and r = n) or d = 2, and n = 2r or 2r − 1.

D_n

¹D_n

Full name: ¹D^(d)
_n,r

Image:

Conditions: d = 2^a | 2n, d ≥ 1, rd ≤ n, n ≠ rd + 1.

Distinguished vertices: d, 2d,...,rd.

Description: Algebraic group: If k has characteristic ≠ 2, the special unitary group SU_2n/d(D,h), where D is a division algebra of degree d over k and h is a hermitian form of discriminant 1 and index r, relative to a k-linear involution σ of D, an "involution of the first kind such that the subring D^σ has dimension d(d + 1)/2; or equivalently, when d > 1 and char k ≠ 2, the group SU_2n/d where D and h are as above except that h is anti-hermitian form of discriminant 1 and index r, and D has dimension d(d − 1)/2.

Special fields: Over a finite field, d = 1 and n = r; over the reals, d = 1 and n − r = 2m, or d = 2 and n = 2r; over a p-adic field or local function field, d = 1 and r = n or n − 2, or d = 2 and n = 2r or 2r + 3; over a number field, d = 1 and n − r = 2m, or d = 2 and n − 2r = 2m or 3; over a totally imaginary number field or a global function field, d=1 and n-r=0,2, or d=2 and n-2r=0,3.

²D_n

Full name: ²D^(d)
_n,r

Image:

Conditions: d = 2^a | 2n, d ≥ 1, rd ≤ n-1.

Distinguished vertices: d, 2d,...,rd. The last one is replaced by (n-1,n) when n=rd+1.

Description: Algebraic group: The same as for ¹D^(d)
_n,r, except that all forms in question have now discriminant ≠ 1.

Special fields: Over a finite field, d=1, n=r+1; over the reals, d=1,n-r=2m+1 or d=2,n=2r+1. Over a p-adic or local function field, d=1,n =r+1, or d=2, n-2r=1,2,3; over a real number field, d=1,r is arbitrary, d=2,n-2r=1,2,3, if D is non-split over the reals, and d=2,r arbitrary, if D is split over the reals. Over a totally imaginary number field or global function field, d=1,n-r=2,4 or d=2,n-2r=1,2,3.

³D²⁸
_4,0

Image:

Special fields: This type exists only over some number fields; does not exist over the finite fields, local fields nor global function fields.

⁶D²⁸
_4,0

Image:

Special fields: This type exists only over some number fields; does not exist over the finite fields, local fields nor global function fields.

³D⁹
_4,1

Image:

Special fields: This type exists only over some number fields; does not exist over the finite fields, local fields nor global function fields.

⁶D⁹
_4,1

Image:

Special fields: This type exists only over some number fields; does not exist over the finite fields, local fields nor global function fields.

³D²
_4,2

Image:

Special fields: This type exists over any finite field, any local non-archimedean and global field; does not exist over the reals.

⁶D²
_4,2

Image:

Special fields: This type exists over any local non-archimedean and global field; does not exist over the finite fields nor the reals.

E₆

¹E⁷⁸
_6,0

Image:

Special fields: This type exists only over some number fields; does not exist over the finite fields, local fields nor global function fields.

¹E²⁸
_6,2

Image:

Special fields: This type exists only over the reals and over some number fields; does not exist over any finite field nor over any local non-archimedean field nor global function field.

¹E¹⁶
_6,2

Image:

Special fields: This type exists only over some local non-archimedean and global fields; does not exists over the finite fields nor the reals.

¹E⁰
_6,6

Image:

Special fields: This type exists over any field.

²E⁷⁸
_6,0

Image:

Special fields: This type exists only over the reals and over some number fields; does not exist over any finite field nor over any local non-archimedean field nor global function field.

²E³⁵
_6,1

Image:

Special fields: This type exists only over some number fields; does not exist over the reals, any finite field nor over any local field nor global function field.

²E²⁹
_6,1

Image:

Special fields: This type exists only over some number fields; does not exist over the reals, any finite field nor over any local field nor global function field.

²E^16'
_6,2

Image:

Special fields: This type exists only over the reals and over some number fields; does not exist over any finite field nor over any local non-archimedean field nor global function field.

²E^16"
_6,2

Image:

Special fields: This type exists only over some number fields; does not exist over any finite field nor over any local field nor global function field.

²E²
_6,4

Image:

Special fields: This type exists over any finite field, any local and global field.

E₇

E¹³³
_7,0

Image:

Special fields: This type exists only over the reals and over some number fields; does not exist over any finite field nor over any local non-archimedean nor global function field.

E⁷⁸
_7,1

Image:

Special fields: This type does not exist over any finite field nor any local nor global field.

E⁶⁶
_7,1

Image:

Special fields: This type does not exist over any finite field nor over any local nor global field.

E⁴⁸
_7,1

Image:

Special fields: This type does not exist over any finite field nor any local nor global fields.

E³¹
_7,2

Image:

Special fields: This type exists only over some number fields; does not exists over any finite field, nor any local nor global field.

E²⁸
_7,3

Image:

Special fields: This type exists only over the reals and over some number fields; ; does not exists over any finite field, nor local non-archimedean nor global function fields.

E⁹
_7,4

Image:

Special fields: This type does not exist over any finite field; it exists over any local and global field.

E⁰
_7,7

Image:

Special fields: This type exists over any field.

E₈

E²⁴⁸
_8,0

Image:

Special fields: This type exists only over the reals and over some number fields; does not exists over any finite field, nor local non-archimedean nor global function fields.

E¹³³
_8,1

Image:

Special fields: This type does not exist over any finite field nor over any local nor global field.

E⁹¹
_8,1

Image:

Special fields: This type does not exist over any finite field nor over any local nor global field.

E⁷⁸
_8,2

Image:

Special fields: This type does not exist over any finite field nor over any local nor global field.

E⁶⁶
_8,2

Image:

Special fields: This type does not exist over any finite field nor over any local nor global field.

E²⁸
_8,4

Image:

Special fields: This type exists only over the reals and over some number fields; does not exists over finite fields, local non-archimedean nor global function fields.

E⁰
_8,8

Image:

Special fields: This type exists over any field.

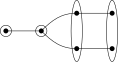
F₄

F⁵²
_4,0

Image:

Description: Algebraic Group: The automorphism group of an exceptional simple Jordan algebra J that does not contain nonzero nilpotent elements.

Special fields: This type exists only over the reals and over some number fields; does not exist over finite fields, local non-archimedean nor global function fields.

F²¹
_4,1

Image:

Description: Algebraic Group: The automorphism group of an exceptional simple Jordan algebra J containing nonzero nilpotent elements, no two of which are nonproportional and orthogonal.

Special fields: This type exists only over the reals and over some number fields; does not exist over any finite field, nor local non-archimedean nor global function field.

F⁰
_4,4

Image:

Description: Algebraic Group: The automorphism group of an exceptional simple Jordan algebra J containing nonproportional orthogonal nilpotent elements.

Special fields: This type exists over any field.

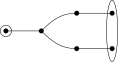
G₂

A group of type G₂ is always the automorphism group of an octonion algebra.

G¹⁴
_2,0

Image:

Description: Algebraic group: the automorphism group of a division octonion algebra.

Special fields: This type exists over the reals and some number fields; does not exist over any finite field, nor local non-archimedean nor global function field.

G⁰
_2,2

Image:

Description: Algebraic group: the automorphism group of a split octonion algebra.

Special fields: This type exists over any field.

References

• Jacobson, Nathan (1939), "Cayley numbers and simple Lie algebras of type G", Duke Mathematical Journal, 5: 775–783, doi:10.1215/s0012-7094-39-00562-4
• Satake, I. (1971), Classification theory of semisimple algebraic groups (with an appendix by M. Sugiura), New York: Marcel--Dekker, pp. viii+149, MR 0316588
• Satake, I. (2001), "On classification of semisimple algebraic groups", Class Field Theory - Its centenary and prospect (Tokyo, 1998) (Advances Studies in Pure Math. vol. 30), Tokyo: Math. Soc. Japan, pp. 197–216, MR 1846459

• Selbach, M. (1976), Klassifikationstheorie der halbeinfacher algebraischer Gruppen , Bonner Math. Schriften, No. 83, Bonn: Universitat Bonn, MR 0432776
• Springer, Tonny A. (1998) [1981], Linear Algebraic Groups (2nd ed.), New York: Birkhäuser, ISBN 0-8176-4021-5, MR 1642713
• Sury, B. (2012), What is the Tits index and how to work with it (www.isibang.ac.in/~sury/titsclassbeam.pdf)
• Thắng, N. Q. (2022), "On the Tits indices of absolutely almost simple algebraic groups over local and global fields", Journal of Pure and Applied Algebra, 226 (9), doi:10.1016/j.jpaa.2022.107031, MR 4379334

• Tits, Jacques (1966), "Classification of algebraic semisimple groups", Algebraic Groups and Discontinuous Subgroups (Proc. Sympos. Pure Math., Boulder, Colo., 1965), Providence, R.I.: American Mathematical Society, pp. 33–62, MR 0224710