Descartes snark
Appearance
| Descartes snark | |
|---|---|
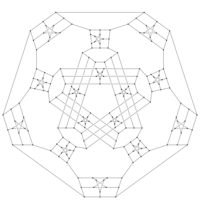 Image of a Descartes snark. | |
| Named after | Blanche Descartes |
| Vertices | 210 |
| Edges | 315 |
| Girth | 5 |
| Chromatic index | 4 |
| Properties | Cubic Snark |
| Table of graphs and parameters | |
In the mathematical field of graph theory, a Descartes snark is an undirected graph with 210 vertices and 315 edges. It is a snark, a graph with three edges at each vertex that cannot be partitioned into three perfect matchings. It was first discovered by William Tutte in 1948 under the pseudonym Blanche Descartes.[1]
A Descartes snark is obtained from the Petersen graph by replacing each vertex with a nonagon and each edge with a particular graph closely related to the Petersen graph. Because there are multiple ways to perform this procedure, there are multiple Descartes snarks.
References
[edit]- ^ Descartes, Blanche (1948), "Network-colourings", The Mathematical Gazette, 32: 67–69, doi:10.2307/3610702, JSTOR 3610702, MR 0026309
