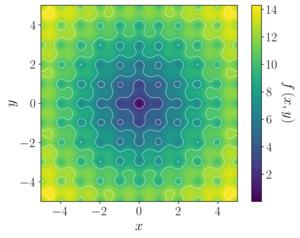
Ackley function

Ackley function of two variables

Contour surfaces of Ackley's function in 3D

In mathematical optimization, the Ackley function is a non-convex function used as a performance test problem for optimization algorithms. It was proposed by David Ackley in his 1987 PhD dissertation. The function is commonly used as a minimization function with global minimum value 0 at 0,.., 0 in the form due to Thomas Bäck. While Ackley gives the function as an example of "fine-textured broadly unimodal space" his thesis does not actually use the function as a test.

For $d$ dimensions, is defined as

$f(x)=-a\exp \left(-b{\sqrt {{\frac {1}{d}}\sum _{i=1}^{d}x_{i}^{2}}}\right)-\exp \left({\frac {1}{d}}\sum _{i=1}^{d}\cos(cx_{i})\right)+a+\exp(1)$

Recommended variable values are $a=20$, $b=0.2$, and $c=2\pi$.

The global minimum is $f(x^{*})=0$ at $x^{*}=0$.

See also

• Test functions for optimization