Jump to content

Wavelet packet decomposition

From Wikipedia, the free encyclopedia

Originally known as optimal subband tree structuring (SB-TS), also called wavelet packet decomposition (WPD; sometimes known as just wavelet packets or subband tree), is a wavelet transform where the discrete-time (sampled) signal is passed through more filters than the discrete wavelet transform (DWT).

Introduction

[edit]

In the DWT, each level is calculated by passing only the previous wavelet approximation coefficients (cAj) through discrete-time low- and high-pass quadrature mirror filters.[1][2] However, in the WPD, both the detail (cDj (in the 1-D case), cHj, cVj, cDj (in the 2-D case)) and approximation coefficients are decomposed to create the full binary tree.[3][2][4][5][6][7]

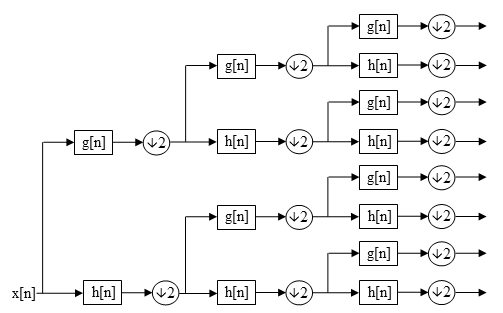
Wavelet packet decomposition over 3 levels. g[n] are the low-pass approximation coefficients, h[n] are the high-pass detail coefficients.

For n levels of decomposition the WPD produces 2n different sets of coefficients (or nodes) as opposed to (n + 1) sets for the DWT. However, due to the downsampling process the overall number of coefficients is still the same and there is no redundancy.

From the point of view of compression, the standard wavelet transform may not produce the best result, since it is limited to wavelet bases that increase by a power of two towards the low frequencies. It could be that another combination of bases produce a more desirable representation for a particular signal.[5] There are several algorithms for subband tree structuring that find a set of optimal bases that provide the most desirable representation of the data relative to a particular cost function (entropy, energy compaction, etc.).[1] [2] There were relevant studies in signal processing and communications fields to address the selection of subband trees (orthogonal basis) of various kinds, e.g. regular, dyadic, irregular, with respect to performance metrics of interest including energy compaction (entropy), subband correlations and others. [4] [6] [7]

Discrete wavelet transform theory (continuous in the time variable) offers an approximation to transform discrete (sampled) signals. In contrast, the discrete-time subband transform theory enables a perfect representation of already sampled signals.[5][8]

[edit]
  • Daubechies D12 packet functions
    Daubechies D12 packet functions
  • Their Fourier spectra
    Their Fourier spectra

Applications

[edit]
  • Wavelet packets were successfully applied in preclinical diagnosis.[9]
  • Wavelet packet decomposition proves advantageous for capturing intricate patterns and variations in the electrochemical signals, which can be indicative of the battery's health and degradation over time. By breaking down the complex battery signal into its constituent frequency components, wavelet packet decomposition allows for a more detailed analysis of the underlying characteristics associated with different stages of battery aging.[10]
  • Wavelet packet decomposition is employed as a preprocessing step to decompose vibration signals acquired from the wind turbine gearbox into multiple frequency bands, capturing both high and low-frequency components. This decomposition allows for the extraction of essential features related to fault signatures at different scales, enabling a more comprehensive analysis of the gearbox's health status. It helps to improve the accuracy and efficiency of fault detection and classification, especially in the complex and critical domain of wind turbine gearbox systems.[11]
  • In the context of rainfall forecasting, wavelet packet decomposition proves valuable for capturing the complex and multi-scale patterns in precipitation data. It can decompose the original monthly rainfall time series into various sub-series corresponding to different frequency. This decomposition is instrumental in unveiling hidden patterns and trends within the data, which can be crucial for improving the forecasting accuracy. [12]
  • Moisture detection in timber is crucial for assessing its structural integrity and preventing potential issues such as decay and damage. Wavelet Packet Decomposition is a powerful signal processing technique that offers a multi-resolution analysis of the timber's moisture content. This approach allows for a detailed examination of the signal at different frequency bands, providing a more comprehensive understanding of the moisture distribution within the material.[13]
  • Researchers employ wavelet packet decomposition to analyze the seismic response of structures, enabling a finer resolution in both time and frequency domains. This detailed analysis allows for the identification of subtle changes in the structural response that may signify damage. By decomposing the seismic response into its constituent frequency components, the researchers gain insights into the time-varying characteristics of the structural behavior. This is crucial for identifying dynamic changes in the structure's response over time, which may indicate the presence and extent of damage.[14]
  • In the context of forecasting oil futures prices, the multiresolution nature of wavelet packet decomposition enables the forecasting model to capture both high and low-frequency components in the time series, thereby improving the ability to capture the complex patterns and fluctuations inherent in financial data.[15]

References

[edit]
  1. ^ a b Coifman R. R. & Wickerhauser M. V., 1992. Entropy-Based Algorithms for Best Basis Selection, IEEE Transactions on Information Theory, 38(2).
  2. ^ a b c A. N. Akansu and Y. Liu, On Signal Decomposition Techniques, (Invited Paper), Optical Engineering Journal, special issue Visual Communications and Image Processing, vol. 30, pp. 912–920, July 1991.
  3. ^ Daubechies, I. (1992), Ten lectures on wavelets, SIAM.
  4. ^ a b H. Caglar, Y. Liu and A. N. Akansu, Statistically Optimized PR-QMF Design, Proc. SPIE Visual Communications and Image Processing, vol. 1605, pp. 86–94, 1991.
  5. ^ a b c A. N. Akansu and R. A. Haddad, Multiresolution Signal Decomposition: Transforms, Subbands, and Wavelets. Boston, MA: Academic Press, ISBN 978-0-12-047141-6, 1992.
  6. ^ a b A. Benyassine and A. N. Akansu, Performance Analysis and Optimal Structuring of Subchannels for Discrete Multitone Transceivers , Proc. IEEE International Symposium on Circuits and Systems (ISCAS), pp. 1456–1459, April 1995.
  7. ^ a b M. V. Tazebay and A. N. Akansu, Adaptive Subband Transforms in Time-frequency Excisers for DSSS Communications Systems, IEEE Trans. Signal Process., vol. 43, pp. 2776–2782, Nov. 1995.
  8. ^ A. N. Akansu, W. A. Serdijn, and I. W. Selesnick, Wavelet Transforms in Signal Processing: A Review of Emerging Applications, Physical Communication, Elsevier, vol. 3, issue 1, pp. 1–18, March 2010.
  9. ^ Zhang, Y.; Dong, Z. (2015). "Preclinical Diagnosis of Magnetic Resonance (MR) Brain Images via Discrete Wavelet Packet Transform with Tsallis Entropy and Generalized Eigenvalue Proximal Support Vector Machine (GEPSVM)". Entropy. 17 (4): 1795–1813. Bibcode:2015Entrp..17.1795Z. doi:10.3390/e17041795.
  10. ^ Ding, Pan; Liu, Xiaojuan; Li, Huiqin; Huang, Zequan; Zhang, Ke; Shao, Long; Abedinia, Oveis (2021). "Useful life prediction based on wavelet packet decomposition and two-dimensional convolutional neural network for lithium-ion batteries". Renewable and Sustainable Energy Reviews. 148. doi:10.1016/j.rser.2021.111287.
  11. ^ Huang, D.; Zhang, W. -A.; Guo, F.; Liu, W.; Shi, X. (12 November 2021). "Wavelet Packet Decomposition-Based Multiscale CNN for Fault Diagnosis of Wind Turbine Gearbox". IEEE Transactions on Cybernetics. 53 (1): 443–453. doi:10.1109/TCYB.2021.3123667. PMID 34767518.
  12. ^ Wang, W.; Wang, Y.; Chau, K.; Liu, C.; Ma, Q. (2021). "A Comparison of BPNN, GMDH, and ARIMA for Monthly Rainfall Forecasting Based on Wavelet Packet Decomposition". Water. 13 (20): 2871. doi:10.3390/w13202871.
  13. ^ Yuan, Cheng; Zhang, Jicheng; Chen, Lin; Xu, Jia; Kong, Qingzhao (10 February 2021). "Timber moisture detection using wavelet packet decomposition and convolutional neural network". Smart Materials and Structures. 30 (3): 035022. Bibcode:2021SMaS...30c5022Y. doi:10.1088/1361-665X/abdc08.
  14. ^ He, Haoxiang; Chen, Yifei; Lan, Bingji (2021). "Damage assessment for structure subjected to earthquake using wavelet packet decomposition and time-varying frequency". Structures. 34: 449–461. doi:10.1016/j.istruc.2021.07.087.
  15. ^ Wang, Jie; Wang, Jun (2021). "A New Hybrid Forecasting Model Based on SW-LSTM and Wavelet Packet Decomposition: A Case Study of Oil Futures Prices". Computational Intelligence and Neuroscience. 2021: 1–22. doi:10.1155/2021/7653091. PMC 8292043. PMID 34335724.
[edit]
Retrieved from "https://en.wikipedia.org/w/index.php?title=Wavelet_packet_decomposition&oldid=1237726036"