User:Mbgale 1/sandbox

Blog

Week One:

This week I created a Wikipedia account and got familiar with some of the policies and guidelines of Wikipedia, along with basic editing information. Everything so far seems pretty straight forward, and I hope I'll be able to make good edits.

Chinese Mathematics Editing

In the Han Dynasty, numbers were developed into a place value decimal system and used on a counting board with a set of counting rods called chousuan, consisting of only nine symbols with a blank space on the counting board representing zero. Negative numbers and fractions were also incorporated into solutions of the great mathematical texts of the period. The mathematical texts of the time, the Suàn shù shū and the Jiuzhang suanshu solved basic arithmetic problems such as addition, subtraction, multiplication and division. Furthermore, they gave the processes for square and cubed root extraction, which eventually was applied to solving quadratic equations up to the third order. Both texts also made substantial progress in Linear Algebra, namely solving systems of equations with multiple unkowns. The value of pi is taken to be equal to three in both texts. However, the mathematicians Liu Xin (d. 23) and Zhang Heng (78–139) gave more accurate approximations for pi than Chinese of previous centuries had used. Mathematics was developed to solve practical problems in the time such as division of land or problems related to division of payment. The Chinese did not focus on theoretical proofs based on geometry or algebra in the modern sense of proving equations to find area or volume. The Book of Computations and The Nine Chapters on the Mathematical Art provide numerous practical examples that would be used in daily life.

Suan shu shu

The Suàn shù shū (Writings on Reckoning or The Book of Computations) is an ancient Chinese text on mathematics approximately seven thousand characters in length, written on 190 bamboo strips. It was discovered together with other writings in 1984 when archaeologists opened a tomb at Zhangjiashan in Hubei province. From documentary evidence this tomb is known to have been closed in 186 BC, early in the Western Han dynasty. While its relationship to the Nine Chapters is still under discussion by scholars, some of its contents are clearly paralleled there. The text of the Suan shu shu is however much less systematic than the Nine Chapters, and appears to consist of a number of more or less independent short sections of text drawn from a number of sources. Some linguistic hints point back to the Qin dynasty.

The Book of Computations contains many perquisites to problems that would be expanded upon in The Nine Chapters on the Mathematical Art. An example of the elementary mathematics in the Suàn shù shū, the square root is approximated by using an "excess and deficiency" method which says to "combine the excess and deficiency as the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them as the dividend." Furthermore, The Book of Computations solves systems of two equations and two unknowns using the same excess and deficiency method.

The Nine Chapters on the Mathematical Art

The Nine Chapters on the Mathematical Art is a Chinese mathematics book, its oldest archeological date being 179 AD (traditionally dated 1000 BC), but perhaps as early as 300–200 BC. Although the author(s) are unknown, they made a huge contribution in the eastern world. Problems are set up with questions immediately followed by answers and procedure. There are no formal mathematical proofs within the text, just a step by step procedure. The commentary of Liu Hui provided geometrical and algebraic proofs to the problems given within the text.

The Nine Chapters on the Mathematical Art was one of the most influential of all Chinese mathematical books and it is composed of some 246 problems. It would later be incorporated into The Ten Mathematical Classics which would become the core of mathematical education in later centuries. This book includes 246 problems on surveying, agriculture, partnerships, engineering, taxation, calculation, the solution of equations, and the properties of right triangles. The Nine Chapters made significant additions to solving quadratic equations in a way similar to Horner's Method. It also made advanced contributions to "fangcheng" or what is now known as linear algebra. Chapter seven solves system of linear equations with two unknowns using the excess and deficit method, similar to The Book of Computations. Chapter eight deals with solving determinate and indeterminate simultaneous linear equations using positive and negative numbers, with one problem dealing with solving four equations in five unknowns. The last problem in the chapter involves four equations in five unknowns, and the topic of indeterminate equations was to remain a favorite among Oriental peoples. The Nine Chapters solves systems of equations using methods similar to the the modern methods of Gaussian elimination and back substitution.

Calculation of Pi

The calculation of pi is often used to gauge the mathematical capabilities of a society. Problems in The Nine Chapters on the Mathematical Art take pi to be equal to three in calculating problems related to circles and spheres, such as spherical surface area. There is no explicit formula given within the text for the calculation of pi to be three, but it is used throughout the problems of both The Nine Chapters on the Mathematical Art and the Artificer's Record, which was produced in the same time period. Historians believe that this figure of pi was calculated using the 3:1 relationship between the circumference and diameter of a circle. Some Han mathematicians attempted to improve this number, such as Liu Hsin, who is believed to have estimated pi to be 3.154. There is no explicit method or record of how he calculated this estimate.

Division and Root Extraction

Basic arithmetic processes such as addition, subtraction, multiplication and division were present before the Han Dynasty. The Nine Chapters on the Mathematical Art take these basic operations for granted and simply instruct the reader to preform them. Han mathematicians calculated square and cubed roots in a similar manner as division, and problems on division and root extraction both occur in Chapter Four of The Nine Chapters on the Mathematical Art. Calculating the squared and cubed roots of numbers is done through successive approximation, the same as division, and often uses similar terms such as dividend (shi) and divisor (fa) throughout the process. This process of successive approximation was then extended to solving quadratics of the second and third order, such as $x^{2}+a=b$, using a method similar to Horner's Method. The method was not extended to solve quadratics of the nth order during the Han Dynasty, however, this method would eventually be used to solve these equations.

Linear Algebra

The Book of Computation is the is the first known text to solve systems of equations with two unknowns. There are a total of three sets problems within The Book of Computation involving solving systems of equations with the excess and deficit method, and again are put into practical terms. Chapter Seven of The Nine Chapters on the Mathematical Art also deals with solving a system of two equations with two unknown with the excess and deficit method. To solve for the greater of the two unknowns, the excess and deficit method instructs the reader to cross multiply the minor terms or "zi" (which are the values given for the excess and defict) with the major terms "mu". To solve for the lesser of the two unknowns, simply add the minor terms together.

Chapter Eight of The Nine Chapters on the Mathematical Art deals with solving infinite equations with infinite unknowns. This process is referred to as the "fangcheng procedure" throughout out the chapter. Many Historians chose to leave the term fangcheng untranslated due to conflicting evidence of what the term means. Many historians refer translate the word to Linear Algebra today. In this chapter, the process of Gaussian Elimination and back substitution are used to solve systems of equations with many unknowns. Problems were done on a counting board and included the use of negative numbers as well as fractions. The counting board was effectively a matrix, where the top line is the first variable of one equation and the bottom was the last.

Liu Hui's Commentary on The Nine Chapters on the Mathematical Art

Liu Hui's π algorithm

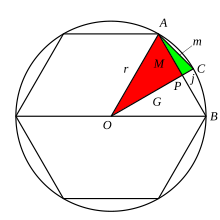
Liu Hui's commentary on The Nine Chapters on the Mathematical Art is the earliest edition of the original text available. Hui is believed by most to be a mathematician shortly after the Han dynasty. Within his commentary, Hui qualified and proved some of the problems from either and algebraic or geometrical standpoint. For instance, throughout The Nine Chapters on the Mathematical Art the value of pi is take to be equal to three in problems regarding circles or spheres. In his commentary, Liu Hui finds a more accurate estimation of pi using the exhaustion method. The exhaustion method involves creating successive polynomials within a circle so that eventually the area of a higher order polygon will be identical to the circle. From this method, Liu Hui asserted that the value of pi is about 3.14. Liu Hui also presented a geometric proof of square and cubed root extraction similar to the Greek Method, which involved cutting a square or cube in any line or section and determining the square root through symmetry of the remaining rectangles.

Global Silver Trade Editing

Notes

peru mexico silver

-mid 16th to end of colonial 100k tons of silver

-peru potosi richest mining

-meixco had better long term growth, higher ore grades/lower costs

-mita system in peru

-growth rate in 1559-1627 from invention of mercury process to reine medium/low grade ores (potosi)

-debate over european inflation due to excess of silver

-drop off in 17th cent

-mex dif curve

-peru depression in 17th ore depletion/high cost = silver less

-tax higher in peru than mexico (quinto vs diezmo)

-potosi cycle 910

-zacatecas 913

-mercury production/ crown monopoly/ huancavelica

-most expensive factor of production

-mita in 1570 (labor draft) 924

silver trade

-manila outpost for connecting Am and Asia

-Japan primary exporter of silver in lathe 16th early 17th

-trade roots for Euro desire for silk/porc

-5.5 mil pesos in Am or Philip via pacific trade

-silver double value in china

-gold out of china

-overuse of paper led to silver in china

manila silver

-silk from china had 2 routes, 1 to japan, 2 to america

-china produced 2.5k tons silk per year in 17th

-japan via manila dominant route

-decentralized production, but tax incentivized

-portugese at macao in 1555, access to chinese markets for jap

-dutch east india company took place in 1640

-exhaustion of jap silver--> new world new source

-silk to america

global economic unity

-1640 bimetallic ratio becomes similar to Euro

-ming paper money failure led to the silver tax system

-chinese pop growth (155 mil 1500, 268 mil 1650)

-dispute over whether europeans made more profit

-smuggling of pesos, buenos aires ports to jap (millions of them)

-exchanged for smuggled african slaves

-population growth due to new crops

-18th cent pop boom new silver demand (mexico)

-mex/peru mining boom

-india played a transit role

-european desire for chinoiserie and tea

-british rise to dominance in 18th c

-tea/ opium cycle

-battle of plassey 1757, brit control of bengal

-silver played lesser role

reorient

-gold moved south, silver north in india

-spa am silver arrived in 17th around cape of good hope

-spanish wanted monopoly

-china sink for silver

-cowries in africa (slaves)

-india exported food (rice, pulses, vegetable oil) to west

-re-exported silver and hoarded

-southeast asia natual crossroads

colonial silver mining

-1550's miners in mex amalgamation

-systems of labor

-all am silver from mountain ranges from canada to chile

-more deep shaft mining in Mexico

-1631 gunpowder for blasting

-1530's German miners introduced stamp mill and lead smelting

-native dominance of mining proces from 1545 to 1572

-separation of silver fast in mexico

-2 to 1 ratio of mercury to silver

-mita 1574

china monetary

-state inability to produce copper led to silver demand

-reverse paper policy, adopt silver

-counterfeit of locally made coin

-commercial revolution in early 16th

ming monetary

-cycles of overprinting, hyperinflation

-counterfeit

The global silver trade between the Americas and Europe from the sixteenth to nineteenth centuries was a spillover of the Columbian Exchange which had a profound effect on the world economy. In fact, many scholars consider the silver trade to mark the beginning of a genuinely global economy, with one historian noting that silver "went round the world and made the world go round." Although global, much of that silver ended up in the hands of the Chinese, as they accepted it as a form of currency. In addition to the global economic changes the silver trade engendered, it also put into motion a wide array of political transformations in the early modern era.

Spaniards traveling west during the Age of Exploration discovered vast amounts of silver, much of which was from the Potosí silver mines, to fuel their trade economy. Potosí's deposits were rich and Spanish American silver mines were the world's cheapest sources of it. The Spanish acquired the silver, minting it into the peso de ocho (a currency) to then use it as a means of purchase; that currency was so widespread that even the United States accepted it as valid until the Coinage Act of 1857. As the Spanish need for silver increased, new innovations for more efficient extraction of silver were developed, such as the amalgamation method of using mercury to extract silver from ore. Still, extracting silver from the New World had a human toll: tens of thousands of workers were forced to extract silver under horrendous conditions. A Spanish priest observed:

In the two centuries that followed the discovery of Potosí, the Spanish silver mines in the Americas produced 40,000 tons of silver. Altogether, more than 150,000 tons of silver were shipped from Potosí by the end of the 18th century. From 1500 to 1800, Mexico and Peru produced about 80% of the world's silver with 30% of it eventually ending up in China (largely because of British merchants who used it to purchase exotic Chinese commodities). In the late 16th and early 17th century, Japan was also exporting heavily into China and the foreign trade at large.

As has been demonstrated, China dominated silver imports. The market value of silver in the Ming territory was double its value elsewhere, which provided great arbitrage profit for the Europeans and Japanese. The abundance of silver in China made it easy for the country to mint it into coinage. That process was so widespread that local Chinese government officials would demand taxes to be paid in silver to the point that silver eventually backed all of China's economy. As the increasing supply of silver from the Spanish and other European powers caused the price of silver to inflate, however, China's over-reliance on that precious metal eventually fueled the Ming Dynasty's collapse.

Silver in the Americas

A result of the Spanish Colonization of the New World was the need for production of metals. The Spanish, along with other European nations, had a great desire for Chinese goods such as silk and porcelain. The Europeans did not have any goods or commodities which China desired, so they traded silver to make up for their trade deficit. The two most important mining colonies of the Spanish Empire were Peru and Mexico, who were estimated to have provided one-hundred thousand tons of silver from the mid 16th Century to the end of the colonial period. The richest, and most productive mine in the Americas was that of Potosi in what is modern day Peru. The richest camp in Mexico was in the city Zacatecas, however the production of this mine was far less than that of Potosi.

Mining Processes in the Americas

More simplistic native mining techniques dominant American mining for the early part of the 16th Century. Mining in the Americas became formally industrialized when the process of mercury amalgamation became popularized. Mercury amalgamation was invented by a Spaniard in central Mexico in the 1550's. Historians dispute what individual was the first to invent the process, however most agree that it was a Spaniard. Mercury was the one of the highest costs of production for the Americas, since much of it had to be shipped. The ratio of Mercury to silver produced was about two to one. Furthermore, German miners introduced the stamp mill and lead smelting in the 1530's. Gunpowder was often used to blast of large holes to create the mine shafts, although there were not many deep shafts. Peru's town of Potosi had the most amount of ore, however it was lower quality than that of Mexico.

Mining production in the Americas largely depended on native labor in both Mexico and Peru. In Mexico, many of the natives worked as wage laborers by the middle of the 17th Century. However, the labor system known as the repartimiento still existed in some places. Silver production in Mexico was relatively cheap when compared to that of Peru, and the general trend of Mexican labor systems was that towards waged labor. In Peru mines, the mita system was a dominant form of native labor subjection, although waged laborers worked on the mines as well. Natives under the mita system were paid much less, and this was necessary for the production of silver to continue in Peru where costs were relatively high.

Global Flow of Silver

The ultimate destination for the mass amounts of silver produced in the Americas and Japan was China. Gold from the Americas flowed mostly across the Atlantic and made its way to the far east. A popular route was around the Cape of Good Hope into the east, and sometimes it came over land. Major outposts for the silver trade were located in Southeast Asian countries, such as the Philippines. The city of Manilla served as a primary outpost of the exchange of goods between the Americas, Japan, and China. However, there is a large amount of silver that crossed across the Pacific Ocean directly from the Americas as well. There are not many records of the amount of silver which crossed the pacific due to it being discouraged by the Spanish monarchy, so estimates highly vary.

Silver also found its was across other parts of the world as well. India and Europe both received a fair amount of silver. This silver was often locally traded for other commodities, such as gold or crops. In India, silver flowed from the south to the north, and gold flowed the opposite way. Often silver and gold were manufactured into jewelry or hoarded as treasure. This is not unique to any particular region.

China and the Demand for Silver

China was the ultimate destination in which silver would flow towards. In exchange, the Chinese traded their popular goods such as silk and porcelain. China had a high demand for silver due to its shift from paper money to coins in the early period of the Ming Dynasty. The Ming paper currency eventually failed due to self imposed inflation along with a inability to stop the production of counterfeit bills. The Ming attempted to produce copper coins as a new form of currency, but production was inconsistent. Hence silver became of high value because it was a valid currency that could be processed abroad. The bimetallic ratio of silver to gold was about two to one, which meant that European and Japanese merchants made a large amount of profit. In the 1640's, the bimetallic ratios in China converged with the rest of the world, before experiencing another population boom. The new population boom was a product of the introduction of New World crops into China, mainly sweet potatoes, which could be more easily grown. By this time, the silver mines in Japan were largely depleted and the New World became China's primary source for silver.

Initially, Japan served as China's primary source for silver in the 16th Century. In exchange for silver, China would provide Japan with silk and gold. Japan and China did not directly trade with each other, due to political tensions. This meant that European entities and countries, such as the Dutch and Portuguese served as a middle man between the two countries.

Contents

[hide]

• 1First paper money
• 2Opium Wars
• 3See also
• 4References

First paper money

The world's first paper money ("flying money") was invented by the Chinese and they needed some commodity to back it. Traditional coins were useful, but the amount of coins needed for large purchases could be bulky and dangerous to transport. That problem was solved when the Chinese created small pieces of paper with pictures of the coin printed on them. By the nature of their geography, China had no real amount of precious metals of their own to back the paper money they invented. Because the Spaniards didn't find gold but did find copious amounts of silver, the Spaniards and the rest of Europe used this silver to purchase the commodities of choice from China, solving both of their problems.

Opium Wars

Main article: Opium Wars

Despite some restrictions, silver continued to drive trade through its popularity in Europe. This, combined with a high British demand for Chinese tea, created chronic trade deficits for European governments, which were forced to risk silver deficits to supply merchants in Asia. As supplies of silver decreased in Europe, Europeans had less ability to purchase highly-coveted Chinese goods. Merchants were no longer able to sustain the China trade through profits made by selling Chinese goods in the West and were forced to take bullion out of circulation in Europe to buy goods in China.

In the 19th century, American merchants began to introduce opium to Chinese markets. The demand for opium rose rapidly and was so profitable that Chinese opium dealers began to seek out more suppliers of the drug, thus inaugurating the opium trade; one merchant declared that Opium "is like gold. It can sell any time." From 1804 to 1820, a period when the Qing Dynasty needed to finance the suppression of the White Lotus Rebellion, Chinese merchants were soon exporting silver to pay for opium rather than Europeans paying for Chinese goods with the precious metal.

The Qing imperial court debated whether and how to end the opium trade, eventually settling on regulations on consumption. That measure, however, resulted in an increase in drug smuggling by Europeans and Chinese traders. In 1810, the Daoguang Emperor issued an edict concerning the matter, declaring, "Opium has a harm. Opium is a poison, undermining our good customs and morality. Its use is prohibited by law." Following a debate at court in 1836 on whether to legalize the drug or crack down on its use, the emperor decided on the latter. An upright official, Commissioner Lin Zexu led the campaign against opium as a kind of "drug czar." The British, offended by the seizure of their property in opium, sent a large naval expedition to China to end the restrictive conditions under which they had long traded with that country. Thus began the first Opium War, in which Britain's industrialized military might was proven in China's rout. The Treaty of Nanking, which ended the war in 1842 largely on British terms, imposed numerous restrictions on Chinese sovereignty and opened five ports to European traders.