User:MRFS/Article02

Tantalising Triangles (in progress)

Once upon a time there was a mathematical analyst who was very perplexed and unhappy because he had found the same answer to two seemingly unrelated problems :-

Problem 1

Three towns are situated at the vertices of a triangle with sides x, y, z. Find the shortest length L of railway track needed to link them together.

Problem 2

The distances from a certain point to the vertices of an equilateral triangle with side L are x, y, z. Find L.

The analyst calculated that L² = (x² + y² + z² + 4Δ√3)/2 where Δ is the area of the triangle with sides x, y, z. This formula applies except in the somewhat obtuse case whenever one of the angles in the first problem exceeds 120°. It is then most economical to lay the track along the two lesser sides of the triangle. Unfortunately for the analyst his methods failed to provide any clues as to why both problems should have the same answer. He concluded that it must either be sheer coincidence or else there must be some subtle means of transforming one problem into the other, so he decided to seek help from one of his bright young engineering students. For the reader's benefit the salient features of his methods are briefly recorded here.

Solution to Problem 1

Fig 1.   Angles at the Fermat point.

Let P be that point within the triangle ABC where u+v+w is minimum. Applying a small perturbation ds to P at an angle θ to AP and ignoring second order terms gives du = ds cos θ , dv = − ds cos(α+θ) , dw = − ds cos(β−θ) .

For (u+v+w) to be minimum (du+dv+dw) must be non-negative for all θ ; in other words cos θ − cos(α+θ) − cos(β−θ) ≥ 0 for 0° ≤ θ ≤ 360° . Putting θ = 90° gives sin α ≥ sin β whilst θ = 270° gives sin α ≤ sin β . Thus sin α = sin β and hence α = β = 60° . The cosine rule then gives v² + vw + w² = x² and w² + wu + u² = y² and u² + uv + v² = z² .

Also Δ is the sum of the areas of the triangles BPC, CPA, APB which is (vw+wu+uv)√3 / 4 . Since L = u + v + w the formula can now be verified directly   ■

Solution to Problem 2

Fig 2.   Distances to the vertices.

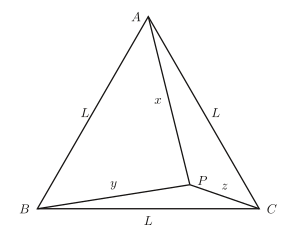
By the cosine rule cos ∠BPC = (y² +z² −L²)/(2yz) and similar expressions exist for cos ∠CPA and cos ∠APB. Recall the identity cos²α + cos²β + cos²γ = 1 + 2 cos α cos β cos γ whenever α + β + γ = 360°. Substituting in this for the three cosines gives a cubic equation for L² in which the absolute term is zero. Once L² has been factored out the discriminant of the resultant quadratic reduces to 4Δ√3 and the formula may now be deduced quite easily   ■

His student suggested that in order to test the possibility of transforming one problem into the other it might be useful to look at some practical examples. In particular she thought it would be fun to seek a solution with x, y, z, L integers. She soon discovered the improper solution 3, 5, 7, 8 (improper since the 3, 5, 7 triangle contains an angle of exactly 120°). She conjectured that there would be no proper integer solutions, but much to her surprise her personal computer quickly produced several, namely 57, 65, 73, 112 and 73, 88, 95, 147. From the first one she developed an infinite number of solutions by observing that 65 is exactly midway between 57 and 73, and then seeking solutions with x = y − t and z = y + t . Using the standard formula for the area of a triangle in terms of its sides she deduced that

$\scriptstyle \Delta ={\frac {1}{4}}\left(y{\sqrt {3}}{\sqrt {y^{2}-4t^{2}}}\right)$     and     $\scriptstyle L^{2}={\frac {1}{2}}\left(3y^{2}+2t^{2}+3y{\sqrt {y^{2}-4t^{2}}}\right).$

Clearly y² − 4t² had to be a perfect square so, following Pythagoras, she wrote y = m² +n² , t = mn.

This gave L² = 3m⁴ + 4m²n² hence L would be an integer provided 3m² + 4n² was a perfect square. Writing m = 4pq , n = |p² − 3q²| gave her plenty of solutions, many of them improper, but by fixing n = 1 an infinite number of proper solutions was assured. This was duly done by solving the Pell equation p² − 3q² = 1. The solutions are (2,1), (7,4), (26,15), ..... where if (p,q) is a solution then ( 2p+3q , p+2q ) is the next one in the series. The first pair yields the computer solution, and the student drew two diagrams of this solution corresponding to the two original problems.

Fig 3.   The two problems compared.

She now remarked that, although she obviously could not measure all the angles with total accuracy, it appeared that each of the three angles between the 57 and 73 lines, the 57 and 65 lines, and the 65 and 73 lines was 60° larger in the second diagram than the first. Now if α is the angle between the y and z lines in the first problem then cos α = (y² +z² −x² )/(2yz) and sin α = 2 Δ /(yz). By the usual formula cos(α + 60°) = (y² +z² −L² ) /(2yz) which, being precisely the cosine of the angle between the y and z lines in the second problem, duly confirmed her suspicion and showed that the 60° difference would hold for every solution to the two problems.

The analyst pretended that he was not in the least impressed by her discovery. After all the fundamental problem of how to transform one problem into the other still remained. Against his better judgement he very reluctantly proposed that they show the local Euclid what they had done and ask for his advice ......

The old professor did not seem particularly pleased to see them. He was in the middle of writing a difficult paper, "On the construction of right-angles", based on the peculiar fact that the diagonals of a quadrilateral intersect at 90° if and only if the sums of the squares of the opposite sides are equal. Minimisation problems were not really his scene, and he was on the point of nodding off when the analyst happened to mention an angle of 120°. All of a sudden he sprang to his feet and began working on his blackboard at incredible speed.

"Surely you are aware of the extension of Ptolemy's Theorem which states that the product of the diagonals of a quadrilateral is less than or equal to the sum of the products of opposite sides with equality if and only if the quadrilateral is cyclic? If not you will find it in any elementary text book."

He paused for breath and glared at his audience as though expecting a reaction. None was forthcoming so he continued. "Given a triangle ABC construct the equilateral triangle BCD (with A and D on opposite sides of BC) and its circumcircle. If P is any point whatsoever then PD.BC ≤ PB.CD + PC.BD hence PD ≤ PB + PC with equality if and only if P lies on the circle. Now AD ≤ PA + PD ≤ PA + PB + PC and equality is actually attained when P is at the point where AD cuts the circle. The length of AD must be L and ∠BPC is then, as you correctly surmised, equal to 120°.

Fig 4.   Construction of the Fermat point.

The two supplicants were now paying attention. They were only vaguely aware of Ptolemy's Theorem, and neither had ever heard of the quoted extension. However the professor had just shown them a simple way to construct the point P , and he was clearly winding up for his finale. "Now construct two more equilateral triangles ACE and ABF . By the same token the lengths of BE and CF are both L , the three lines AD, BE, CF all meet at that point P which minimises PA + PB + PC and the angle between any two of these lines is 60°."

Fig 5.   Shows the problems are isomorphic.

"Now construct the parallelogram AZBE. Since AD = BE = AZ and ∠ZAD = 60° it follows that AZD is an equilateral triangle with side L. Moreover the distances from B to the vertices of AZD are precisely BC (because BC = BD), CA (because CA = AE = BZ), and AB. Thus your first problem has been transformed into your second one. QED and goodbye." "Muddling bumpkins", muttered the professor to himself as the analyst and the student made their way down his drive. "That youngster would believe black was white if a computer said so, and the other's a born troublemaker - always asking stupid questions and poking his nose in where it doesn't belong. They should stick to what they're good at and steer clear of mathematics."

As soon as they were out of earshot of the house the analyst turned to his companion. "That man's attitude is quite intolerable. How he ever got that chair is beyond me. His ilk have never forgiven us analysts for putting a stop to their circle-squaring antics." "You may be right", replied the young student, "but at least he solved our problem. I don't suppose you yourself have ever considered any further training in Euclidean geometry?" The analyst recoiled in horror. "You must be joking" he snapped. "As far as modern mathematics is concerned Euclidean geometry is very stale beer indeed." He glanced at his watch. "Ten to three already. Time for some fresh scones and honey would you say?"