Talk:P-adic number
| This is the talk page for discussing improvements to the P-adic number article. This is not a forum for general discussion of the article's subject. |
Article policies
|
| Find sources: Google (books · news · scholar · free images · WP refs) · FENS · JSTOR · TWL |
| Archives: 1Auto-archiving period: 12 months |
| This It is of interest to the following WikiProjects: | |||||||||||
| |||||||||||
|
This page has archives. Sections older than 365 days may be automatically archived by Lowercase sigmabot III when more than 10 sections are present. |
Section "Introduction"
[edit]I removed the section "Introduction" with the edit summary "rm the section as WP:OR, confusing, and/or out of scope: As 10 is not prime, the "10-adic absolute value" that is considered here is not an absolute value, and the strange resulting properties do not help to understand the subject of the article". This has been reverted.
So I have tagged the section, and explain here whic this section must be removed. This section is aimed to introduce the subject of the article which is p-adic numbers. In the literature, these numbers are defined only when p is prime. So, introducing the subject with p = 10 is already confusing, as 10 is not prime. Moreover, the fact that 10 is not prime induces complications that makes the introduction harder to understand than the subject of the article, and leads to nonsensical assertions, such the definition of an "absolute value" that is explicitly said to not be an absolute value (moreover this caveat is in a footnote, and this makes the section even more confusing for readers who do not spent time to open footnotes).
I intended to remove this section again, but it appeared to me that the whole article has similar issues. Especially, I have not found any workable definition of p-adic integers and p-adic numbers. So, I'll add the lacking information before removing the present mess. D.Lazard (talk) 12:15, 30 May 2021 (UTC)
Section „p-adic series”
[edit]The new section defines the coefficients by
- «every is a rational number such that the denominator is not divisible by p».
This is certainly a possibility, but done without any reference ― and completely new to me. In all books I know of, the p-adic coefficients are already integers although not all necessarily in the interval Knuth e.g. likes very much the coefficients from the interval for an approach which he calls balanced ternary and which is a Teichmüller representation using the -st roots of unity as digits. All such representations are certainly p-adic series, as well.
Other books start with the p-adic valuation or absolute value without going the side step with these coefficients.
Besides that, there is derived an equivalence relation which IMHO is far less important than the equivalence relation which is established by the sequences converging to 0, which means that equivalent sequences (or series) have the same p-adic limit. ―Nomen4Omen (talk) 20:06, 6 June 2021 (UTC)
- I do not intend to use p-adic series for the representation of p-adic numbers. I'll use only the normalized p-adic series. However general p-adic series are needed for defining operations on p-adic numbers, specially for division of p-adic numbers.
- Presently, the article does not contain any understandable definition of p-adic numbers. Definitions are given only in the sixth section, needs advanced concepts such as inverse limits, or general notions of topology (completion). Moreover the equivalence of these definitions is not mentioned. Also many properties that make p-adic numbers fundamental for number theory are completely lacking: they form an extension field of the rationals that is locally compact; the term of discrete valuation is completely lacking, except in a quotation hidden in a footnote; etc.
- In summary, something is "far more important" than anything else, which is to provide a definition of p-adic numbers and a description of their main properties that is accessible to the largest possible audience. I am working on this, and this is for this reason that I have added the section "p-adic series". D.Lazard (talk) 08:56, 7 June 2021 (UTC)
- Very good that you do not intend to use p-adic series for the representation of p-adic numbers.
- But certainly, your p-adic series is NOT needed for defining operations on p-adic numbers, even not for division of p-adic numbers.
- You still do not give a reference for your «p-adic series».
- Pls do not misunderstand me: I do not want to defend the previous version. I fully agree with your goal: to provide a definition of p-adic numbers and a description of their main properties that is accessible to the largest possible audience. ―Nomen4Omen (talk) 15:43, 7 June 2021 (UTC)
- I would like to emphasize my remark 2: There exist people (I'm not among them) who find p-adic operations of rational numbers, especially division, better than calculations with numerator and denominator !! And they do that absolutely without your unnormalized p-adic series. So again: What shall your «unnormalized p-adic series» be good for ?? ―Nomen4Omen (talk) 16:52, 7 June 2021 (UTC)
Now it is about a week that I asked you: What is your «unnormalized p-adic series» good for ?
"In this talk", let me call it the „unnormalized p-adic series of D.Lazard type“.
In your edit dated 12 June 2021 08:45 you have added: «every rational number can be considered as a p-adic series» (as I stimulated you in this talk's section Valuation first) ― so what is the gain in introducing these unnormalized p-adic series of D.Lazard type ? Since I would like to assume that you have something in mind with them, it would only be fair to your WP-readers that you tell them what it is. Just to make further speculations superfluous and the discussion simpler. ―Nomen4Omen (talk) 09:43, 13 June 2021 (UTC)
- General p-adic series are unavoidables as soon as one compute with p-adic numbers, since the normalized p-adic series are not closed under series operations (addition, subtraction, multiplication, division, etc.). The series operations applied to normalized p-adic series provide general p-adic series. So the question is not "What is «unnormalized p-adic series» good for", it is "Is there a reasonable way to define and describe operations on p-adic numbers, without using unnormalized p-adic series and without entering into the technical details of carry management? D.Lazard (talk) 15:26, 13 June 2021 (UTC)
- I thought that everybody knows that the standard (in your words the normalized) p-adic series ARE closed under addition, subtraction, multiplication, division. I am sure that you know this as well: Isn't a field
- containing all rational numbers and all numbers, you are talking about (the unnormalized p-adic series of D.Lazard type), and
- being closed under these operations ??
- From your post I have to assume that you don't like carry management. But also with your unnormalized p-adic series of D.Lazard type it is impossible to avoid it. Take e.g. and add, then you have and you have to manage some carry. And I'm sure that you can't avoid it when you want to show some equivalence:
- A very simple thing for you could be to pinpoint to an operation (addition, subtraction, multiplication, division) and to related operands which are not closed. ―Nomen4Omen (talk) 16:07, 13 June 2021 (UTC)
- and are normalized 5-adic series. Their difference as series is
- This is a 5-adic series, but not a normalized one. One must normalize it for getting the difference as a 5-adic numbers. D.Lazard (talk) 17:18, 13 June 2021 (UTC)
- By the way, I do not like so much the introduction of p-adic numbers through p-adic series. But the representation of p-adic numbers as p-adic series is implicit in their positional notation, and this positional notation is used in many introducing textbook. As Wikipedia must be based on a solid mathematical foundation, p-adic series must appear soon in the article. It is possible to avoid series, by defining a p-adic integer as a sequence such that, for every i, and is the image of under the canonical map (this is the definition of the p-adic numbers as an inverse limit). I'll detail this approach in a section entitled "Modular properties". This is important as this is widely used for fast integer and rational computation (exact linear algebra), and polynomial factorization. D.Lazard (talk) 17:18, 13 June 2021 (UTC)
- and are normalized 5-adic series. Their difference as series is
- I thought that everybody knows that the standard (in your words the normalized) p-adic series ARE closed under addition, subtraction, multiplication, division. I am sure that you know this as well: Isn't a field
- In many introducing textbooks, p-adic numbers are identified with p-adic series of your normalized type. And it is possible to define arithmetics (addition, subtraction, multiplication, division) on these series of your normalized type and to show that this arithmetic coincides for rational numbers with the standard arithmetic ― very much similar to the teachers for decimal arithmetic at school. These definitions and proofs are on solid mathematical foundations and there is no need to talk about inverse limits nor about modular properties, but ―yes― carry management is needed. [Several times I have tried to pinpoint you to the very strange Quote notation: these people even replace (numerator,denominator)-arithmetics by p-adic series ― and try to convince the whole world that theirs is better.] Btw, you did not yet really show how solid your mathematical foundations are: for me and up to now, the usefulness of the unnormalized p-adic series of D.Lazard type is hot air including the arithmetics on them. I can agree that some positional p-adic notation appears soon in the article and I have decided to wait, although your latest post does not help me very much.
- Btw, I threw out your remark on the size of the base, because you are far away from showing an example where a problem about the size of the digits shows up.
- ―Nomen4Omen (talk) 18:34, 13 June 2021 (UTC)
Section „p-adic series” is WP:OR=Original Research
[edit]@D.Lazard: As it appears you have finished working on this article. So I insert some amendments which make clear that not everything is clear, especially this section „p-adic series”. At the beginning you inserted 20:45, 9 June 2021 "formal series". So I convert this to standard notation. [Additionally I have to write "evaluated at point X=p".] As you possibly see: Your set of p-adic series is not the Formal power series as the standard user is insinuated to assume. And it is absolutely not obvious and has to be proved explicitly that your equivalence relation comprises all rational numbers. ―Nomen4Omen (talk) 09:32, 20 June 2021 (UTC)
- It is wrong to say that using formal series for defining p-adic numbers is WP:OR, as many textbooks use formal series for defining p-adic numbers. The definition/representation of p-adic numbers as infinite sequences of digits use formal series implicitly and cannot be made formally correct without formal series.
- The definition of p-adic series is explicitly restricted to this article, it has been introduced for convenience of writing. It would be WP:OR only if this was presented as a standard definition.
- By the way, I have edited Formal power series for including the general definition of a power series. This is not WP:OR, as the completion of a local ring is often defined by using formal series with a term in each degree of the associated graded ring. This is not the case in WP, where the more technical use of inverse limit has been preferred. D.Lazard (talk) 11:26, 20 June 2021 (UTC)
- @D.Lazard: You saw my remark and reverted it. But this is NOT AT ALL an answer to my question: How do you find this order (after a mathematical operation) without any evaluation ? ―Nomen4Omen (talk) 13:23, 20 June 2021 (UTC)
Valuation first
[edit]Besides the unresolved issue about the „p-adic series” above, I think it is not a good sequence of explaining some math analysis when the series do run up to infinity without having defined the conditions for convergence. Many books introduce the possible valuations (absolute values) of the rational numbers first, then define a topology, then define limits and completion within, and then (in the case of p-adics) show that all rational numbers (and not only those with p-denominators) are among these convergent series and can if needs be written as infinite p-adic series. –Nomen4Omen (talk) 16:25, 9 June 2021 (UTC)
- Up to now, I have not yet considered any math analysis. Everything that I have written is pure algebra. I have just edited the article for making clear that the p-adic series are formal series, and thus that no convergence has to be considered. In any case circular reasoning must be avoided, and it seems that this is what you are asking for: one cannot define a p-adic number as a limit when the space in which the limit occurs is not yet defined.
- About the terminology, I know that "p-adic series" is not a standard term. This is the reason for introducing them by "in this article". However, the concept is not original research, as my "normalized p-adic series" is exactly the same concept as the "infinite p-adic expansion" widely considered in the article, with the difference that writing the terms of the series as digits makes impossible to work with large prime numbers.
- Also p-adic numbers were introduced for number theory, and most of their applications are in number theory and algebra. So, they must be described in a style adapted for number theorists and algebraists. This was not the case before my edits. D.Lazard (talk) 21:21, 9 June 2021 (UTC)
- If you identify math analysis with real analysis you may be right. But if analysis starts with infinitesimal and infinity then you are wrong, then it is analysis already when you talk about formal series which run to infinity. And you certainly know that the difference between pure algebra and other math does not help you so much.
Your recourse to formal series is a problem especially when you admit coefficients with denominators : as far as I can see the identification of these series with their normalizations can work only if you take non-formal (≈ analytic ??) limits, e.g. when expanding 1/2 for p=3.
You say: «So, the p-adic expansion of a rational number is a normalized p-adic series.» Why that? Isn't the (I admit: unnormalized) 3-adic series a valid 3-adic expansion of the rational number 1/2 ??
You say: «The p-adic valuation, or p-adic order of a nonzero p-adic series is the lowest integer i such that » What if the numerator is divisible by p ??
You do not elaborate true algorithms for addition, subtraction, multiplication, division. - As far as I can see: especially your section «p-adic series» is WP:OR and even a defective one. ―Nomen4Omen (talk) 08:42, 10 June 2021 (UTC)
- Clearly some tweaks are still needed. I have fixed your objection about the numerator multiple of p. Also, I have clarified that the p-adic expansion of a rational number has all its coefficients integers in the interval [0, p − 1).
- An example of computation of a p-adic expansion of a rational number is still lacking. Also, the algorithms are only sketched, but a section detailing them is needed and lacking (even in the old version). D.Lazard (talk) 14:39, 10 June 2021 (UTC)
- If you identify math analysis with real analysis you may be right. But if analysis starts with infinitesimal and infinity then you are wrong, then it is analysis already when you talk about formal series which run to infinity. And you certainly know that the difference between pure algebra and other math does not help you so much.
- I saw your repair wrt. numerator. Indeed, great insight !!
- I'm kind of helpless wrt. your proposed division step consisting of writing for r=1/2 and p=3. What do you propose: a=1 and s=−1/2 or a=0 and s=1/2 ?? Both satisfy , but appear not to satisfy . Or a=2 and s=−3/2 ? Then, what would be the subsequent division step ?? And the 3-adic expansion of 1/2 ?? It is , but how do you get there ? Since these algorithms are all well known and already contained in WP, I'm asking why you do not take them ― and present your phantasy instead ?
- I'm extremely eager to learn about your detailing the «only sketched» algorithms of addition, subtraction, multiplication, division (I do not see a sketch anywhere).
- As it appears in total: you do not have a book where you are taking your texts from.
- As far as I can see the old version recurs to the well-known standard algorithms of finite partial sums and goes to the valid(!) limits. But I agree: this is not really well elaborated, if you do not take the link to the very strange Quote notation. And it has the additional (in my opinion lesser) problem of 10 not being a prime. Finally, it is indeed a question whether starting from decimal standard has to be given up in principle. ―Nomen4Omen (talk) 18:33, 10 June 2021 (UTC)
- If and one has and thus one must have (you forgot this condition in your post). As (Bézout's identity for 2 and 3), one has So and At the next step, one has So, and the process can be repeated infinitely.
- In the end, the end is not visible. So I'll let you time for your elaborations. We both know that the matter is/the matters are settled in principle ― maybe already since 1897.
Remark: I had to correct some process to be repeated indefinitely above.
Best regards. ―Nomen4Omen (talk) 14:16, 11 June 2021 (UTC) - Sorry, I still can't resist: Isn't a finite
- formal series of the form where every nonzero is a rational number such that none of and is divisible by p
- already a kind of your «p-adic series», and a simpler one ??
Pls note that it has the additional advantage that its arithmetics is taught in school !! ―Nomen4Omen (talk) 14:42, 11 June 2021 (UTC)
- In the end, the end is not visible. So I'll let you time for your elaborations. We both know that the matter is/the matters are settled in principle ― maybe already since 1897.
Trying to rescue the section „p-adic expansion of rational numbers”
[edit]- Bind r to the formula.
- Bind s to its role in the iteration.
- Remove misplaced "with the order of digits reversed".
- Make the value of s explicit.
- Not the order of the digits is reversed, but their production wrt. significance.
- Make explicit the "integer part".
- The sign in has to be omitted.
- Show the order of the digits in the standard notation.
―Nomen4Omen (talk) 18:33, 23 June 2021 (UTC)
Plase didactic examples
[edit]For example for P-adic_number#p-adic_integers is not evident how to use . Suppose p=2 and x as the first natural numbers...
x | x1 | x2 | x3 | x4
-------+----+----+----+----
1 | ? | ? | ? | ?
2 | ? | ? | ? | ?
3 | ? | ? | ? | ?
...
8 | ? | ? | ? | ?
...
Please show a list of valid values as example.
Alternative definition is valid?
[edit]This Gupta's link has a, perhaps, didactic definition for p-adic integers, that is not used but is valid:
- where p is a prime and the are integers from {0, 1, . . . , p− 1}. So, seems the positional notation.
The reader can understand that, for p=2, the valid are in {0,1}
- ... the simple (but in reversed order) classic binary representation. Is it?
Now, returning to the article's definition of p-adic_integers, how to obtain a valid ? It is non-obvious in the article. And, if the Gupta's definition is valid, how to relate the two representations? they are equivalent? Krauss (talk) 14:38, 23 July 2023 (UTC)
- I agree that the article is awfully written. I have rewritten the lead for having a clear (and as elementary as possible) definition of p-adic numbers and integers.
- As it is, the article contains a method for computing the coefficients of the normalized p-adic series of a rational number, but, to be found, it requires a careful reading of the article.
- Also, it is only for positive integers that p-adic representation resembles to positional notation. For example, for every p, the p-adic representation of –1 is D.Lazard (talk) 13:31, 24 July 2023 (UTC)
- That example still resembles positional notation, to any programmer familiar with two's complement. —David Eppstein (talk) 18:02, 24 July 2023 (UTC)
- I took a shot at a more accessible first sentence, but folks should feel free to adapt or rewrite it for clarity/style. Can we find any existing materials aimed at laypeople which have a clear 1–2 sentence summary? –jacobolus (t) 20:21, 26 July 2023 (UTC)
OOOPS
[edit]The order of the sections was confusing. In particular, the p-adic expansion of a rational number into a p-adic series was described before the definition of a p-adic series. So, I have written a section "p-adic series". This is only after publishing it that I saw that a section existed already with this title, in a style that resemble to mine. In fact, it is myself who partially wrote the section two year ago.
So, these two sections need to be merged, and I will do this soon. However, the old section contains some mistakes. Mainly that, with the chosen definition of p-adic series, the sum of two p-adic series is not always a p-adic series. D.Lazard (talk) 16:48, 16 August 2023 (UTC)
 Done. The subsequent sections still require to be updated and upgraded. D.Lazard (talk) 15:00, 19 August 2023 (UTC)
Done. The subsequent sections still require to be updated and upgraded. D.Lazard (talk) 15:00, 19 August 2023 (UTC)
Lead image
[edit]
I'm disappointed by the removal of the previous lead image (shown at right) in this August edit: [1]. I created the image, so I'm biased! But I think there's a lot of value in having a lead image that is compelling and, dare I say, pretty. And I want to emphasize that the image isn't some flight-of-fancy original research on my part. It's just the solenoidal embedding of the p-adic integers. The description for the full-size image cites Chistyakov (1996), but you can find similar images in the dynamical systems literature even before that.
I'm open to improving the image to have more explanatory value, although at the outset, I want to warn that there's only so much explanation that is possible in a lead image. The image description page has plenty of room for explanatory text, but the image itself doesn't, nor does the caption. It's asking too much of the lead image to fully explain the topic to a general-audience reader with no background.
That said, I think the most straightforward improvement would be to label the selected group elements. I could embed, in the image, labels like:
- 0 = 0_3
- 9 = 100_3
- 3 = 10_3
- 1 = 1_3
- −1/8 = …0101_3 (edit: this was wrong in the original comment)
- −1/2 = …111_3
- 1/4 = …2021_3
- −1/4 = …0202_3
- 1/2 = …1112_3
- 1/8 = …2122_3
- −1 = …222_3
- −3 = …2220_3
- −9 = …22200_3
Such labels would have the nice benefit of reinforcing the lead paragraph's discussion of digit expansions. They would make the whole image larger, so to avoid losing detail, I would want to increase the WP:THUMBSIZE by 50% or so.
@D.Lazard: Before I go to the trouble of putting such an SVG together, what do you think? Of course, other editors' opinions are also welcome. Melchoir (talk) 00:34, 2 October 2023 (UTC)
- One general request (not specific to this image): can people please choose colors that are less colorful than #00F, #0F0, #F00, etc.? If anyone needs help choosing a color scheme I am happy to offer more concrete advice based on whatever constraints are relevant to the particular image. –jacobolus (t) 01:27, 2 October 2023 (UTC)
- Wikipedia Manual of Style says
Images must be significant and relevant in the topic's context, not primarily decorative. They are often an important illustrative aid to understanding
. Here, the image caption involves advanced knowledge of the theory of topological groups, which are not supposed to be known by readers; even for people who know the involved concepts, the relationship between p-adic numbers and elements of the figure is far to be obvious. So, the image is definitively not an "illustrative aid to understand" p-adic numbers, and it is only "decorative" for most readers. Moreover, it is very confusing, as suggesting that the group structure (additive or multiplicative?) is more fundamental than the field structure. - However, if a section would be added on the characters of the group of p-adic numbers, such an image could be used to illustrate the section. If such a section is eventually added, the image must be in that section, not in the lead.
- About your suggested modification of the image, I doubt that it will make the image clearer for the lay reader. Moreover, I do not understand how you intend to label nodes of a finite tree (this is the nature of the image) with infinite 3-adic expansions.
- D.Lazard (talk) 09:34, 2 October 2023 (UTC)
- If there's otherwise no image at all, I think this is too harsh a standard / too harsh an application of the standard. Do you have an idea for a more comprehensible image that would be meaningful to an audience at, say, high school level? If not, an image that flies over some readers heads is still better than nothing. It seems fair enough to call this image significant and relevant, not "primarily decorative", even if it is not immediately obvious to less technical readers. –jacobolus (t) 17:25, 2 October 2023 (UTC)
- There are some examples at this Quanta article that might inspire a slightly more elementary image. –jacobolus (t) 17:36, 2 October 2023 (UTC)
- For a comprehensive image, I would use a rooted ternary tree whose edges are arrows directed toward the root. The nodes of level k should be labeled by the integers from (in decimal notation or in base 3-notation or both) to The arrow from a node of level to a node of level should correspond to the reduction modulo (for example, ). If one stops at, say, the level 3 (27 nodes at this level), one may add some nodes at infinity such as -1, 1/2, -1/2, 5/7, ..., with dotted arrows toward their reduction modulo 27. I suggest to present the image horizontally with the root on the right. Probably, the level 3 would give a to complicate image. This can be solved by stopping at level 2 or considering 2-adic numbers. In any case, 2-adic numbers seem more suitable than 3-adic numbers, as allowing more information with less nodes. Also, readers are probably more accustomed with base 2 than with base 3. D.Lazard (talk) 20:07, 2 October 2023 (UTC)
- There are some examples at this Quanta article that might inspire a slightly more elementary image. –jacobolus (t) 17:36, 2 October 2023 (UTC)
- If there's otherwise no image at all, I think this is too harsh a standard / too harsh an application of the standard. Do you have an idea for a more comprehensible image that would be meaningful to an audience at, say, high school level? If not, an image that flies over some readers heads is still better than nothing. It seems fair enough to call this image significant and relevant, not "primarily decorative", even if it is not immediately obvious to less technical readers. –jacobolus (t) 17:25, 2 October 2023 (UTC)
I restored the image in a flight of passion before reading the talk page. I did not intend to edit war, I am sorry. It is one of my favorite mathematical illustrations. I don't think the criticisms of the image are strong enough to warrant its deletion. D.Lazard criticizes the image for labelling infinite p-adic representations on an illustration only showing finite digits, but in his own proposed illustration he still must cut an infinite representation short, which is the very nature of these things. Even if the lay reader does not understand the whole image, the middle section is a very clear illustration of the topology of the p-adics. The SVG even tagged the balls, which are not clear in the article space, perhaps this is to be remedied somehow. The picture is striking and Pontryagin Duality gives a geometric association to a subject which too easily could appear overly formal to the lay reader. The color pallete is completely in line with those used in 3d complex plots, with argument represented by a value on a color wheel. These are often hailed as stunning visuals that get people intrigued in a number system initially beyond their intuition, even if the plots can stay largely mysterious. There is another illustration using 2-adic numbers. It's a good one, but 90-degree angles are some of the most recognized and can lead to some confusion as to groupings as the groupings can easily be inferred to be in groups of 4 (of course filtering the limit to powers of 4 changes nothing about the 2-adic integers, but that is not the most natural way of thinking about them). Hence I think 3 is a better choice. Qsdd (talk) 22:42, 2 October 2023 (UTC)

- Thanks for the comments! I'm not as active on Wikipedia as I used to be, so I might not be able to respond to every point of discussion. Just a couple of things to clarify:
- * The 2-adic version is shown at the right. It has roughly the same formal content, but I agree with Qsdd that the 3-adic image is better. In part, this is because the 2-adic version makes the black points sparser (lower Hausdorff dimension), so the 2-adic numbers are less visually salient than the metric balls and the selected duals. The lead image for an article about the p-adic numbers should put some set of p-adic numbers front and center, so that's an important consideration in favor of the 3-adic version.
- * (Also, the simple fraction 1/2 is not a 2-adic integer, which is a shame. I think the elements −1/2 and 1/2 are the most visually stunning elements of the 3-adic integers in the 3-adic image. The 2-adic image shows −1/3 and 1/3, but the colored discs for those are much less comprehensible, in my opinion.)
- * Regarding how my above proposal for labeling would work, the idea is simply that the image already picks out a few representative 3-adic integers to label, namely 0, 9, 3, 1, −1/8, −1/2, 1/4, −1/4, 1/2, 1/8, −1, −3, and −9. Those labels are already explained in the image description page. The proposal is merely to embed the labels in the content of the image, as well. There is no need to worry about infinite digit expansions, since the selected elements are all rational numbers with repeating expansions, which I wrote down above. Melchoir (talk) 00:29, 3 October 2023 (UTC)
color pallete is completely in line with those used in 3d complex plots
– this may be, but that's because those complex plots (what Wegert calls phase portraits) have an incredibly poorly chosen color scheme (which is not surprising: the color scheme was barely "chosen" at all, but rather was the easiest thing to implement for various mathematicians/programmers who had no background whatsoever in visual art, design, or vision science). The problems with it are that (1) the colors create visual artifacts that are not relevant to the data, (2) the colors hide visual features of the data that should be presented, (3) the color relationships give misleading visual impression of data relationships, and perhaps especially (4) the colors are so intense that they are visually distracting and unpleasant (perhaps even physically uncomfortable) to look at. One of my medium term goals is to take my painfully slow Matlab code that generates dramatically better phase portraits than the ones found around the web, and properly reimplement it in a browser to render using a GPU. Ricky Reusser implemented something like my ideas here but I don't think all of the details are quite right yet. Once that is sorted I'd like to try to replace as many of the phase portraits found around the world as possible with better ones that more appropriately and pleasantly depict the data they are trying to show. –jacobolus (t) 05:11, 3 October 2023 (UTC)
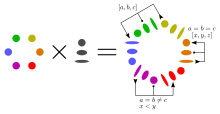
Proof that I don't always use the same colors - Here's the thing about the naive RGB color scheme. In 99% of cases, I would agree with the framing of (1-3) as problems that should be avoided. Just to prove that I'm being sincere, see the illustration on the right, where I didn't use it.
- But if ever there were a time to introduce visual artifacts that emphasize the special role of the cube roots of unity, the diagram of the 3-adic integers would be the time. It is meaningful that certain characters assign certain elements of the dual group to certain cube roots of unity. We want it to be obvious where that happens. The usage of special colors is -- in this one, exceptional case -- a feature, not a bug.
- As for (4), that's more subjective. I could try dialing back the green a bit. Not too much, though, because the variation in lightness serves a mathematical purpose! It helps to communicate the mirror-image relationship between the pinwheel shapes on the right, especially −9 vs 9. The difference in lightness between green and blue makes those characters visually "turn" in opposite directions. If all the colors had the same lightness, I worry that the whole thing would degrade into visual noise. Melchoir (talk) 19:03, 3 October 2023 (UTC)
- The colors absolutely should not all have the same lightness (lightness contrast is the most visually salient for recognizing fine details, and a picture without lightness contrast looks entirely flat and becomes difficult for readers with normal color vision but nearly impossible for readers with color vision deficiencies). However, the lightness used for each color should be deliberately chosen, not just left to the arbitrary primaries used in sRGB. –jacobolus (t) 02:22, 4 October 2023 (UTC)
- Oh interesting, I thought we were going to disagree about lightness contrast, but I'm glad to have been mistaken!
- So... what kind of colors would you suggest? Melchoir (talk) 04:59, 4 October 2023 (UTC)
- The colors absolutely should not all have the same lightness (lightness contrast is the most visually salient for recognizing fine details, and a picture without lightness contrast looks entirely flat and becomes difficult for readers with normal color vision but nearly impossible for readers with color vision deficiencies). However, the lightness used for each color should be deliberately chosen, not just left to the arbitrary primaries used in sRGB. –jacobolus (t) 02:22, 4 October 2023 (UTC)
n-adic numbers when n is not a prime
[edit]What about the case of n-adic numbers when n is not a prime? I've read that:
- When n is a product of two (or more) different primes, the resulting structure has divisors of 0. (For example, in 10-adic numbers there are numbers which correspond to "2^∞" and "5^∞", and (2^∞)*(5^∞) is 0.
- When n is a power of a prime (p^k), n-adic numbers are isomorphic to p-adic numbers. (4-adic numbers are equivalent to 2-adic numbers.)
Mike Rosoft (talk) 09:05, 17 December 2024 (UTC)
- n-adic numbers are generally not defined when n is not prime. However, the construction of p-adic numbers is a specific case of completion with respect to an ideal. The p-adic numbers is the case where the ideal is the cases your are talking about is when the ideal is not prime. Passing from p to amounts to multiply the p-adic absolute value by a constant factor; so, this does not change the completion. It is true also that if there are several minimal prime ideals containing the ideal used for completion, the resulting ring contains zero-divisor.
- This should be mentioned in a section "Generalization", but, unfortunately, no editor took the time for writing this. D.Lazard (talk) 15:23, 17 December 2024 (UTC)





![{\displaystyle [0,p-1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d784d3c09f6c16f2be810fc933b13c064cf70df)
![{\displaystyle [-1,0,+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71581e910fd6e51b3919f5605f01690a81139bd9)















































