Equivalent radius
In applied sciences, the equivalent radius (or mean radius) is the radius of a circle or sphere with the same perimeter, area, or volume of a non-circular or non-spherical object. The equivalent diameter (or mean diameter) () is twice the equivalent radius.
Perimeter equivalent
[edit]
The perimeter of a circle of radius R is . Given the perimeter of a non-circular object P, one can calculate its perimeter-equivalent radius by setting
or, alternatively:
For example, a square of side L has a perimeter of . Setting that perimeter to be equal to that of a circle imply that
Applications:
- US hat size is the circumference of the head, measured in inches, divided by pi, rounded to the nearest 1/8 inch. This corresponds to the 1D mean diameter.[1]
- Diameter at breast height is the circumference of tree trunk, measured at height of 4.5 feet, divided by pi. This corresponds to the 1D mean diameter. It can be measured directly by a girthing tape.[2]
Area equivalent
[edit]

The area of a circle of radius R is . Given the area of a non-circular object A, one can calculate its area-equivalent radius by setting
or, alternatively:
Often the area considered is that of a cross section.
For example, a square of side length L has an area of . Setting that area to be equal that of a circle imply that
Similarly, an ellipse with semi-major axis and semi-minor axis has mean radius .
For a circle, where , this simplifies to .
Applications:
- The hydraulic diameter is similarly defined as 4 times the cross-sectional area of a pipe A, divided by its "wetted" perimeter P. For a circular pipe of radius R, at full flow, this is
- as one would expect. This is equivalent to the above definition of the 2D mean diameter. However, for historical reasons, the hydraulic radius is defined as the cross-sectional area of a pipe A, divided by its wetted perimeter P, which leads to , and the hydraulic radius is half of the 2D mean radius.[3]
- In aggregate classification, the equivalent diameter is the "diameter of a circle with an equal aggregate sectional area", which is calculated by . It is used in many digital image processing programs.[4]
Volume equivalent
[edit]
The volume of a sphere of radius R is . Given the volume of a non-spherical object V, one can calculate its volume-equivalent radius by setting
or, alternatively:
For example, a cube of side length L has a volume of . Setting that volume to be equal that of a sphere imply that
Similarly, a tri-axial ellipsoid with axes , and has mean radius .[5] The formula for a rotational ellipsoid is the special case where . Likewise, an oblate spheroid or rotational ellipsoid with axes and has a mean radius of .[6] For a sphere, where , this simplifies to .
Applications:
- For planet Earth, which can be approximated as an oblate spheroid with radii 6378.1 km and 6356.8 km, the 3D mean radius is .[6]
Other equivalences
[edit]Surface-area equivalent radius
[edit]The surface area of a sphere of radius R is . Given the surface area of a non-spherical object A, one can calculate its surface area-equivalent radius by setting
or equivalently
For example, a cube of length L has a surface area of . A cube therefore has an surface area-equivalent radius of
Curvature-equivalent radius
[edit]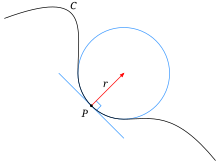
The osculating circle and osculating sphere define curvature-equivalent radii at a particular point of tangency for plane figures and solid figures, respectively.
See also
[edit]- Antenna equivalent radius
- Cloud drop effective radius
- Cubic mean
- Earth ellipsoid
- Earth radius
- Galaxy effective radius
- Geoid
- Geometric mean
- Semidiameter
References
[edit]- ^ Bello, Ignacio; Britton, Jack Rolf (1993). Topics in Contemporary Mathematics (5th ed.). Lexington, Mass: D.C. Heath. p. 512. ISBN 9780669289572.
- ^ West, P. W. (2004). "Stem diameter". Tree and Forest Measurement. New York: Springer. pp. 13ff. ISBN 9783540403906.
- ^ Wei, Maoxing; Cheng, Nian-Sheng; Lu, Yesheng (October 2023). "Revisiting the concept of hydraulic radius". Journal of Hydrology. 625 (Part B): 130134. Bibcode:2023JHyd..62530134W. doi:10.1016/j.jhydrol.2023.130134.
- ^ Sun, Lijun (2016). "Asphalt mix homogeneity". Structural Behavior of Asphalt Pavements. pp. 821–921. doi:10.1016/B978-0-12-849908-5.00013-4. ISBN 978-0-12-849908-5.
- ^ Leconte, J.; Lai, D.; Chabrier, G. (2011). "Distorted, nonspherical transiting planets: impact on the transit depth and on the radius determination" (PDF). Astronomy & Astrophysics. 528 (A41): 9. arXiv:1101.2813. Bibcode:2011A&A...528A..41L. doi:10.1051/0004-6361/201015811.
- ^ a b Chambat, F.; Valette, B. (2001). "Mean radius, mass, and inertia for reference Earth models" (PDF). Physics of the Earth and Planetary Interiors. 124 (3–4): 4. Bibcode:2001PEPI..124..237C. doi:10.1016/S0031-9201(01)00200-X.






















![{\displaystyle R_{\text{eq}}={\sqrt[{3}]{\frac {3V}{4\pi }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/971b336cb40005d8de7260ab4e6468db9f5e7943)

![{\displaystyle R_{\text{eq}}={\sqrt[{3}]{\frac {3}{4\pi }}}L\approx 0.6204L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85bb7558e3541d789b504896a85150076aeceef4)

![{\displaystyle R_{\text{eq}}={\sqrt[{3}]{a\cdot b\cdot c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f4634f961d3bf8cbe1dfb5237da94274448c441)
![{\displaystyle R_{\text{eq}}={\sqrt[{3}]{a^{2}\cdot c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c50910bdf543a7efe98b346f0d5ad4fc5f2dc9fb)

![{\displaystyle R={\sqrt[{3}]{6378.1^{2}\cdot 6356.8}}=6371.0{\text{ km}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d1c9b558e1c6435b432e8536585072a51d0153c)




