Theodolite

A theodolite (/θiˈɒdəˌlaɪt/)[1] is a precision optical instrument for measuring angles between designated visible points in the horizontal and vertical planes. The traditional use has been for land surveying, but it is also used extensively for building and infrastructure construction, and some specialized applications such as meteorology and rocket launching.[2]
It consists of a moveable telescope mounted so it can rotate around horizontal and vertical axes and provide angular readouts. These indicate the orientation of the telescope, and are used to relate the first point sighted through the telescope to subsequent sightings of other points from the same theodolite position. These angles can be measured with accuracies down to microradians or seconds of arc. From these readings a plan can be drawn, or objects can be positioned in accordance with an existing plan. The modern theodolite has evolved into what is known as a total station where angles and distances are measured electronically, and are read directly to computer memory.
In a transit theodolite, the telescope is short enough to rotate about the trunnion axis, turning the telescope through the vertical plane through the zenith; for non-transit instruments vertical rotation is restricted to a limited arc.
The optical level is sometimes mistaken for a theodolite, but it does not measure vertical angles, and is used only for leveling on a horizontal plane (though often combined with medium accuracy horizontal range and direction measurements).
Principles of operation
[edit]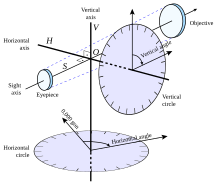
Preparation for making sightings
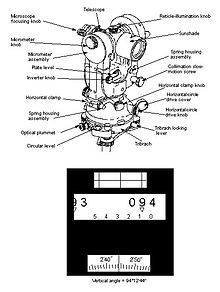
[edit]Temporary adjustments are a set of operations necessary in order to make a theodolite ready for taking observations at a station. These include its setting up, centering, leveling up and elimination of parallax, and are achieved in four steps:
- Setting up: fixing the theodolite onto a tripod along with approximate leveling and centering over the station mark.
- Centering: bringing the vertical axis of theodolite immediately over station mark using a centering plate also known as a tribrach.
- Leveling: leveling of the base of the instrument to make the vertical axis vertical usually with an in-built bubble-level.
- Focusing: removing parallax error by proper focusing of objective and eye-piece. The eye-piece only requires adjustment once at a station. The objective will be re-focused for each subsequent sighting from this station because of the different distances to the target.
Sightings
[edit]Sightings are taken by the surveyor, who adjusts the telescope's vertical and horizontal angular orientation so the cross-hairs align with the desired sighting point. Both angles are read either from exposed or internal scales and recorded. The next object is then sighted and recorded without moving the position of the instrument and tripod.
The earliest angular readouts were from open vernier scales directly visible to the eye. Gradually these scales were enclosed for physical protection, and finally became an indirect optical readout, with convoluted light paths to bring them to a convenient place on the instrument for viewing. The modern digital theodolites have electronic displays.
Errors in measurement
[edit]- Index error
- The angles in the vertical axis should read 90° (100 grad) when the sight axis is horizontal, or 270° (300 grad) when the instrument is transited. Half of the difference between the two positions is called the index error. This can only be checked on transit instruments.
- Horizontal axis error
- The horizontal and vertical axes of a theodolite must be perpendicular; if not then a horizontal axis error exists. This can be tested by aligning the tubular spirit bubble parallel to a line between two footscrews and setting the bubble central. A horizontal axis error is present if the bubble runs off central when the tubular spirit bubble is reversed (turned through 180°). To adjust, the operator removes half the amount the bubble has run off using the adjusting screw, then re-level, test and refine the adjustment.
- Collimation error
- The optical axis of the telescope must also be perpendicular to the horizontal axis; if not, then a collimation error exists.
Index error, horizontal-axis error (trunnion-axis error) and collimation error are regularly determined by calibration and are removed by mechanical adjustment. Their existence is taken into account in the choice of measurement procedure in order to eliminate their effect on the measurement results of the theodolite.
History
[edit]Historical background
[edit]Prior to the theodolite, instruments such as the groma, geometric square and the dioptra, and various other graduated circles (see circumferentor) and semicircles (see graphometer) were used to obtain either vertical or horizontal angle measurements. Over time their functions were combined into a single instrument that could measure both angles simultaneously.
The first occurrence of the word "theodolite" is found in the surveying textbook A geometric practice named Pantometria (1571) by Leonard Digges.[3] The origin of the word is unknown. The first part of the Neo-Latin theo-delitus might stem from the Greek θεᾶσθαι, "to behold or look attentively upon"[4] The second part is often attributed to an unscholarly variation of the Greek word: δῆλος, meaning "evident" or "clear".[5][6] Other Neo-Latin or Greek derivations have been suggested as well as an English origin from "the alidade".[7]
The early forerunners of the theodolite were sometimes azimuth instruments for measuring horizontal angles, while others had an altazimuth mount for measuring horizontal and vertical angles. Gregorius Reisch illustrated an altazimuth instrument in the appendix of his 1512 book Margarita Philosophica.[3] Martin Waldseemüller, a topographer and cartographer made the device in that year[8] calling it the polimetrum.[9] In Digges's book of 1571, the term "theodolite" was applied to an instrument for measuring horizontal angles only, but he also described an instrument that measured both altitude and azimuth which he called a topographicall instrument [sic].[10] Possibly the first instrument approximating to a true theodolite was the built by Josua Habemel in 1576, complete with compass and tripod.[8] The 1728 Cyclopaedia compares "graphometer" to "half-theodolite".[11] As late as the 19th century, the instrument for measuring horizontal angles only was called a simple theodolite and the altazimuth instrument, the plain theodolite.[12]
The first instrument to combine the essential features of the modern theodolite was built in 1725 by Jonathan Sisson.[12] This instrument had an altazimuth mount with a sighting telescope. The base plate had spirit levels, compass and adjusting screws. The circles were read with a vernier scale.
-
Jesse Ramsden's Great Theodolite of 1787
-
A theodolite of 1851, showing the open construction, and the altitude and azimuth scales which are read directly
-
A theodolite of the transit type with six-inch circles, manufactured in Britain c. 1910 by Troughton & Simms
-
Wild T2 theodolite originally designed by Heinrich Wild in 1919
-
Sectioned Wild theodolite showing the complex light paths for optical readout, and the enclosed construction
-
Bundeswehr Zeiss Rk 76 A1 - 1970s
Development of the theodolite
[edit]The theodolite became a modern, accurate instrument in 1787, with the introduction of Jesse Ramsden's famous great theodolite, which he created using a very accurate dividing engine of his own design.[12] Ramsden's instruments were used for the Principal Triangulation of Great Britain. At this time the highest precision instruments were made in England by such makers as Edward Troughton.[13] Later the first practical German theodolites were made by Breithaupt together with Utzschneider, Reichenbach and Fraunhofer.[14]
As technology progressed the vertical partial circle was replaced with a full circle, and both vertical and horizontal circles were finely graduated. This was the transit theodolite. This type of theodolite was developed from 18th century astronomical Transit instruments used to measure accurate star positions. The technology was transferred to theodolites in the early 19th century by instrument makers such as Edward Troughton and William Simms[15] and became the standard theodolite design. Development of the theodolite was spurred on by specific needs. In the 1820s progress on national surveying projects such as the Ordnance Survey in Britain produced a requirement for theodolites capable of providing sufficient accuracy for large scale triangulation and mapping. The Survey of India at this time produced a requirement for more rugged and stable instruments such as the Everest pattern theodolite with its lower center of gravity.
Railway engineers working in the 1830s in Britain commonly referred to a theodolite as a "Transit".[16] The 1840s was the start of a period of rapid railway building in many parts of the world which resulted in a high demand for theodolites wherever railways were being constructed.[17] It was also popular with American railroad engineers pushing west, and it replaced the railroad compass, sextant and octant. Theodolites were later adapted to a wider variety of mountings and uses. In the 1870s, an interesting waterborne version of the theodolite (using a pendulum device to counteract wave movement) was invented by Edward Samuel Ritchie.[18] It was used by the U.S. Navy to take the first precision surveys of American harbors on the Atlantic and Gulf coasts.[19]
In the early 1920s a step change in theodolite design occurred with the introduction of the Wild T2 made by the Swiss Wild Heerbrugg company. Heinrich Wild designed a theodolite with divided glass circles with readings from both sides presented at a single eyepiece close to the telescope so the observer did not have to move to read them. The Wild instruments were not only smaller, easier to use and more accurate than contemporary rivals but also sealed from rain and dust. Canadian surveyors reported that while the Wild T2 with 3.75 inch circles was not able to provide the accuracy for primary triangulation it was the equal in accuracy to a 12 inch traditional design.[20] The Wild T2, T3, and A1 instruments were made for many years.
In 1926 a conference was held at Tavistock in Devon, UK where Wild theodolites were compared with British ones. The Wild product outclassed the British theodolites so manufacturers such as Cooke, Troughton & Simms and Hilger & Watts set about improving the accuracy of their products to match their competition. Cooke, Troughton and Simms developed the Tavistock pattern theodolite and later the Vickers V. 22.[21]
Wild went on to develop the DK1, DKM1, DM2, DKM2, and DKM3 for Kern Aarau company. With continuing refinements, instruments steadily evolved into the modern theodolite used by surveyors today. By 1977 Wild, Kern and Hewlett-Packard were all offering "Total stations" which combined angular measurements, electronic distance measurement and microchip functions in a single unit.
Operation in surveying
[edit]
Triangulation, as invented by Gemma Frisius around 1533, consists of making such direction plots of the surrounding landscape from two separate standpoints. The two graphing papers are superimposed, providing a scale model of the landscape, or rather the targets in it. The true scale can be obtained by measuring one distance both in the real terrain and in the graphical representation.
Modern triangulation as, e.g., practiced by Snellius, is the same procedure executed by numerical means. Photogrammetric block adjustment of stereo pairs of aerial photographs is a modern, three-dimensional variant.
In the late 1780s, Jesse Ramsden, a Yorkshireman from Halifax, England who had developed the dividing engine for dividing angular scales accurately to within a second of arc (≈ 0.0048 mrad or 4.8 μrad), was commissioned to build a new instrument for the British Ordnance Survey. The Ramsden theodolite was used over the next few years to map the whole of southern Britain by triangulation.
In network measurement, the use of forced centering speeds up operations while maintaining the highest precision. The theodolite or the target can be rapidly removed from, or socketed into, the forced centering plate with sub-millimeter precision. Nowadays GPS antennas used for geodetic positioning use a similar mounting system. The height of the reference point of the theodolite—or the target—above the ground benchmark must be measured precisely.
-
Surveying theodolite
-
United States Coast and Geodetic Survey technicians observing with a 0.2 arcsecond (≈ 0.001 mrad or 1 μrad) resolution Wild T3 theodolite mounted on an observing stand. Photo was taken during an Arctic field party (c. 1950).
Transit theodolite
[edit]The term transit theodolite, or transit for short, refers to a type of theodolite where the telescope is short enough to rotate in a full circle on its horizontal axis as well as around its vertical axis. It features a vertical circle which is graduated through the full 360 degrees and a telescope that could "flip over" ("transit the scope"). By reversing the telescope and at the same time rotating the instrument through 180 degrees about the vertical axis, the instrument can be used in 'plate-left' or 'plate-right' modes ('plate' refers to the vertical protractor circle). By measuring the same horizontal and vertical angles in these two modes and then averaging the results, centering and collimating errors in the instrument can be eliminated. Some transit instruments are capable of reading angles directly to thirty arc-seconds (≈ 0.15 mrad). Modern theodolites are usually of the transit-theodolite design, but engraved plates have been replaced with glass plates designed to be read with light-emitting diodes and computer circuitry, greatly improving accuracy up to arc-second (≈ 0.005 mrad) levels.
Use with weather balloons
[edit]There is a long history of theodolite use in measuring winds aloft, by using specially-manufactured theodolites to track the horizontal and vertical angles of special weather balloons called ceiling balloons or pilot balloons (pibal). Early attempts at this were made in the opening years of the nineteenth century, but the instruments and procedures weren't fully developed until a hundred years later. This method was extensively used in World War II and thereafter, and was gradually replaced by radio and GPS measuring systems from the 1980s onward.
The pibal theodolite uses a prism to bend the optical path by 90 degrees so the operator's eye position does not change as the elevation is changed through a complete 180 degrees. The theodolite is typically mounted on a rugged steel stand, set up so it is level and pointed north, with the altitude and azimuth scales reading zero degrees. A balloon is released in front of the theodolite, and its position is precisely tracked, usually once a minute. The balloons are carefully constructed and filled, so their rate of ascent can be known fairly accurately in advance. Mathematical calculations on time, rate of ascent, azimuth and angular altitude can produce good estimates of wind speed and direction at various altitudes.[22]
Modern electronic theodolites
[edit]
In modern electronic theodolites, the readout of the horizontal and vertical circles is usually done with a rotary encoder. These produce signals indicating the altitude and azimuth of the telescope which are fed to a microprocessor. CCD sensors have been added to the focal plane of the telescope allowing both auto-targeting and the automated measurement of residual target offset. All this is implemented in embedded software of the processor.
Many modern theodolites are equipped with integrated electro-optical distance measuring devices, generally infrared based, allowing the measurement in one step of complete three-dimensional vectors—albeit in instrument-defined polar coordinates, which can then be transformed to a preexisting coordinate system in the area by means of a sufficient number of control points. This technique is called a resection solution or free station position surveying and is widely used in mapping surveying.
Such instruments are "intelligent" theodolites called self-registering tacheometers or colloquially "total stations", and perform all the necessary angular and distance calculations, and the results or raw data can be downloaded to external processors, such as ruggedized laptops, PDAs or programmable calculators.[23]
Gyrotheodolites
[edit]A gyrotheodolite is used when the north-south reference bearing of the meridian is required in the absence of astronomical star sights. This occurs mainly in the underground mining industry and in tunnel engineering. For example, where a conduit must pass under a river, a vertical shaft on each side of the river might be connected by a horizontal tunnel. A gyrotheodolite can be operated at the surface and then again at the foot of the shafts to identify the directions needed to tunnel between the base of the two shafts. Unlike an artificial horizon or inertial navigation system, a gyrotheodolite cannot be relocated while it is operating. It must be restarted again at each site.
The gyrotheodolite comprises a normal theodolite with an attachment that contains a gyrocompass, a device which senses the rotation of the Earth in order to find true north and thus, in conjunction with the direction of gravity, the plane of the meridian. The meridian is the plane that contains both the axis of the Earth's rotation and the observer. The intersection of the meridian plane with the horizontal defines the true north-south direction found in this way. Unlike magnetic compasses, gyrocompasses are able to find true north, the surface direction toward the north pole.
A gyrotheodolite will function at the equator and in both the northern and southern hemispheres. The meridian is undefined at the geographic poles. A gyrotheodolite cannot be used at the poles where the Earth's axis is precisely perpendicular to the horizontal axis of the spinner, indeed it is not normally used within about 15 degrees of the pole where the angle between the earth's rotation and the direction of gravity is too small for it to work reliably. When available, astronomical star sights are able to give the meridian bearing to better than one hundred times the accuracy of the gyrotheodolite. Where this extra precision is not required, the gyrotheodolite is able to produce a result quickly without the need for night observations.
See also
[edit]- Manufacturers
References
[edit]- ^ "theodolite". Dictionary.com Unabridged (Online). n.d.
- ^ Thyer, Norman (March 1962). "Double Theodolite Pibal Evaluation by Computer". Journal of Applied Meteorology and Climatology. 1 (1). American Meteorological Society: 66–68. Bibcode:1962JApMe...1...66T. doi:10.1175/1520-0450(1962)001<0066:DTPEBC>2.0.CO;2.
- ^ a b Daumas, Maurice, Scientific Instruments of the Seventeenth and Eighteenth Centuries and Their Makers, Portman Books, London 1989 ISBN 978-0-7134-0727-3
- ^ "Theaomai – Greek Lexicon". Archived from the original on 8 December 2008. Retrieved 15 September 2008.
- ^ "languagehat.com : THEODOLITE". languagehat.com.
- ^ "Take Our Word for It Issue 16". takeourword.com.
- ^ Melivll, E. H. V. (1909). "Derivation of the word "Theodolite"". Nature. 81 (2087): 517–518. Bibcode:1909Natur..81R.517M. doi:10.1038/081517b0. S2CID 3955351.
- ^ a b Colombo, Luigi; Selvini, Attilio (1988). Sintesi di una storia degli strumenti per la misura topografica [Summary of a history of topographic measurement tools] (in Italian). Archived from the original on 13 November 2007.
- ^ Mills, John FitzMaurice, Encyclopedia of Antique Scientific Instruments, Aurum Press, London, 1983, ISBN 0-906053-40-4
- ^ Turner, Gerard L'E., Elizabethan Instrument Makers: The Origins of the London Trade in Precision Instrument Making, Oxford University Press, 2000, ISBN 978-0-19-856566-6
- ^ Cyclopaedia, vol. 2 p. 50 for "Semi-Circle"
- ^ a b c Turner, Gerard L'E. Nineteenth Century Scientific Instruments, Sotheby Publications, 1983, ISBN 0-85667-170-3
- ^ Anita McConnell, Instrument Makers to the World pp. 6–44 ISBN 978-1850720966
- ^ Ralf Kern: Wissenschaftliche Instrumente in ihrer Zeit/Band 4: Perfektion von Optik und Mechanik. Cologne, 2010, pp. 349–360.
- ^ McConnells, Anita (1992). Instrument Makers to the World. Sessions. pp. 6–24. ISBN 978-1850720966.
- ^ Conder, F R (1983). The Men who Built Railways (reprint from 1837). Thomas Telford. pp. 4–56. ISBN 978-0727701831.
- ^ Anita McConnell, Instrument Makers to the World pp. 123–125 ISBN 978-1850720966
- ^ American Academy of Arts and Sciences, Proceedings of the American Academy of Arts and Sciences, Vol. XXIII, May 1895 – May 1896, Boston: University Press, John Wilson and Son (1896), pp. 359–360
- ^ American Academy, pp. 359–360
- ^ Anita McConnell, Instrument Makers to the World pp. 79–80 ISBN 978-1850720966
- ^ Anita McConnell, Instrument Makers to the World pp. 80–82 ISBN 978-1850720966
- ^ Brenner, Martin (25 November 2009). "Pilot Weather Balloon (Pibal) Optical Theodolites". Martin Brenner's Pilot Balloon Resources. California State University, Long Beach. Retrieved 25 July 2014.
- ^ Paiva, Joseph V. (1 October 2004). "The End of An Era - On the genesis, life and death of the HP 48". Point of Beginning (PoB). BNP Media. Retrieved 20 October 2015.
External links
[edit] Media related to Theodolites at Wikimedia Commons
Media related to Theodolites at Wikimedia Commons








