File:VFPt metal balls largesmall potential+contour.svg
Page contents not supported in other languages.
Tools
Actions
General
In other projects
Appearance

Size of this PNG preview of this SVG file: 800 × 600 pixels. Other resolutions: 320 × 240 pixels | 640 × 480 pixels | 1,024 × 768 pixels | 1,280 × 960 pixels | 2,560 × 1,920 pixels.
Original file (SVG file, nominally 800 × 600 pixels, file size: 183 KB)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
| DescriptionVFPt metal balls largesmall potential+contour.svg |
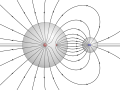
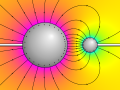
English: Electric field around a large and a small conducting sphere at opposite electric potential. The shape of the field lines is computed exactly, using the method of image charges with an infinite series of charges inside the two spheres. Field lines are always orthogonal to the surface of each sphere. In reality, the field is created by a continuous charge distribution at the surface of each sphere, indicated by small plus and minus signs. The electric potential is depicted as background color with yellow at 0V together with equipotential lines. |
| Date | |
| Source | Own work |
| Author | Geek3 |
| Other versions |
|
| SVG development InfoField | |
| Source code InfoField | Python code# paste this code at the end of VectorFieldPlot 3.1
# https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot
u = 100.0
doc = FieldplotDocument('VFPt_metal_balls_largesmall_potential+contour',
commons=True, width=800, height=600, unit=u)
# define spheres with position and radius
s1 = {'c':sc.array([-1.0, 0.]), 'r':1.5}
s2 = {'c':sc.array([2.0, 0.]), 'r':0.5}
spheres = [s1, s2]
def U_sphere(sphere, charges):
f = Field([ ['monopole', {'x':c['p'][0], 'y':c['p'][1], 'Q':c['Q']}] for c in charges])
return sc.mean([f.V(sphere['c'] + sphere['r'] * array((cos(phi), sin(phi))))
for phi in sc.linspace(0, 2*pi, 64, endpoint=False)])
def Q_sphere(isphere, charges):
return sum([c['Q'] for c in charges if c['i'] == isphere])
# compute series of charges https://dx.doi.org/10.2174/1874183500902010032
def mirrored_charges(p, Q, isphere, spheres, Qmin):
'''
Recursive function. Returns list of mirrored charges for n spheres
'''
if fabs(Q) < Qmin:
return []
charges = [{'p':p, 'Q':Q, 'i':isphere}]
for i, s in enumerate(spheres):
if i != isphere:
pnew = s['c'] + (p - s['c']) * (s['r'] / vabs(p - s['c']))**2
Qnew = -Q * s['r'] / vabs(p - s['c'])
charges += mirrored_charges(pnew, Qnew, i, spheres, Qmin)
return charges
charges_raw = [mirrored_charges(s['c'], 1., si, spheres, 1e-4) for si,s in enumerate(spheres)]
# Use charge normalization from paper above
# Here one can also solve for charge conditions such as neutrality
matrixU = [ [U_sphere(s, cs) for cs in charges_raw] for s in spheres]
matrixQ = [ [Q_sphere(si, cs) for cs in charges_raw] for si in range(len(spheres))]
U0, U1 = 1., -1
charge_factors = sc.linalg.solve(matrixU, [U0, U1])
for il in range(len(charges_raw)):
for ic in range(len(charges_raw[il])):
charges_raw[il][ic]['Q'] *= charge_factors[il]
charges = [c for cl in charges_raw for c in cl]
charges = sorted(charges, key=lambda x: -fabs(x['Q']))
for si, s in enumerate(spheres):
s['U'] = U_sphere(s, charges)
s['Q'] = Q_sphere(si, charges)
#print('sphere', si, s, 'U =', s['U'], 'Q =', s['Q'])
print('using', len(charges), 'mirror charges.')
field = Field([ ['monopole', {'x':c['p'][0], 'y':c['p'][1], 'Q':c['Q']}] for c in charges])
def pot(xy):
for s in spheres:
if vabs(xy - s['c']) <= s['r']:
return s['U']
return field.V(xy)
doc.draw_scalar_field(func=pot, cmap=doc.cmap_AqYlFs, vmin=U1, vmax=U0)
doc.draw_contours(func=pot, linewidth=1, linecolor='#444444',
levels=sc.linspace(U1, U0, 17)[1:-1])
# draw symbols
#for c in charges:
# doc.draw_charges(Field([ ['monopole', {'x':c[0][0], 'y':c[0][1], 'Q':c[1]}] ]),
# scale=0.6*sqrt(fabs(c[1])))
gradr = doc.draw_object('linearGradient', {'id':'rod_shade', 'x1':0, 'x2':0,
'y1':0, 'y2':1, 'gradientUnits':'objectBoundingBox'}, group=doc.defs)
for col, of in (('#666', 0), ('#ddd', 0.6), ('#fff', 0.7), ('#ddd', 0.8),
('#888', 1)):
doc.draw_object('stop', {'offset':of, 'stop-color':col}, group=gradr)
gradb = doc.draw_object('radialGradient', {'id':'metal_spot', 'cx':'0.53',
'cy':'0.54', 'r':'0.55', 'fx':'0.65', 'fy':'0.7',
'gradientUnits':'objectBoundingBox'}, group=doc.defs)
for col, of in (('#fff', 0), ('#e7e7e7', 0.15), ('#ddd', 0.25),
('#aaa', 0.7), ('#888', 0.9), ('#666', 1)):
doc.draw_object('stop', {'offset':of, 'stop-color':col}, group=gradb)
ball_charges = []
for ib, s in enumerate(spheres):
ball = doc.draw_object('g', {'id':'metal_ball{:}'.format(ib+1),
'transform':'translate({:.3f},{:.3f})'.format(*(s['c'])),
'style':'fill:none; stroke:#000;stroke-linecap:square', 'opacity':1})
# draw rods
if ib == 0:
x1, x2 = -4.1 - s1['c'][0], -0.9 * s1['r']
else:
x1, x2 = 0.9 * s2['r'], 4.1 - s2['c'][0]
doc.draw_object('rect', {'x':x1, 'width':x2-x1,
'y':-0.1/1.2+0.01, 'height':0.2/1.2-0.02,
'style':'fill:url(#rod_shade); stroke-width:0.02'}, group=ball)
# draw metal balls
doc.draw_object('circle', {'cx':0, 'cy':0, 'r':s['r'],
'style':'fill:url(#metal_spot); stroke-width:0.02'}, group=ball)
ball_charges.append(doc.draw_object('g',
{'style':'stroke-width:0.02'}, group=ball))
def startpath1(t):
phi = 2. * pi * t
return s2['c'] + 1.5 * array([cos(phi), sin(phi)])
def startpath2(t):
phi = 2. * pi * t
return s1['c'] + s1['r'] * array([cos(phi), -sin(phi)])
nlines1 = 16
startpoints = Startpath(field, startpath1).npoints(nlines1)
nlines2 = 14
startpoints += Startpath(field, startpath2, t0=0.195, t1=1-0.195).npoints(nlines2)
for ip, p0 in enumerate(startpoints):
line = FieldLine(field, p0, directions='both', maxr=7.,
bounds_func=lambda xy: max([s['r'] - vabs(xy-s['c']) for s in [s1, s2]]))
# draw little charge signs near the surface
path_minus = 'M {0:.5f},0 h {1:.5f}'.format(-2./u, 4./u)
path_plus = 'M {0:.5f},0 h {1:.5f} M 0,{0:.5f} v {1:.5f}'.format(-2./u, 4./u)
for si in range(2):
sphere = [s1, s2][si]
# check if fieldline ends inside the sphere
for ci in range(2):
if (vabs(line.get_position(ci) - sphere['c']) < sphere['r'] and
vabs(line.get_position(1-ci) - sphere['c']) > sphere['r']):
# find the point where the field line cuts the surface
t = optimize.brentq(lambda t: vabs(line.get_position(t)
- sphere['c']) - sphere['r'], 0., 1.)
pr = line.get_position(t) - sphere['c']
cpos = (-0.06 + 0.96 * sphere['r']) * vnorm(pr)
doc.draw_object('path', {'stroke':'black', 'd':
[path_plus, path_minus][ci],
'transform':'translate({:.5f},{:.5f})'.format(
round(u*cpos[0])/u, round(u*cpos[1])/u)},
group=ball_charges[si])
arrow_d = 2.0
of = {'start':0.5 + s1['r'] / arrow_d, 'leave_image':0.45,
'enter_image':0.5, 'end':0.5 + s2['r'] / arrow_d}
ar_st = {'dist':arrow_d, 'offsets':of}
if ip >= nlines1:
ar_st = {'potential':pot, 'at_potentials':[0.55*U0]}
ar_st['scale'] = 1.2
doc.draw_line(line, arrows_style=ar_st)
doc.write()
|
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
This file is licensed under the Creative Commons Attribution-Share Alike 4.0 International license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Captions
Electric field around a large and a small sphere at opposite potential
Items portrayed in this file
depicts
30 May 2020
image/svg+xml
187,772 byte
600 pixel
800 pixel
54e62e9609b6e3e900cd1c6e094c0a288b9fbba2
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 12:37, 30 May 2020 |  | 800 × 600 (183 KB) | Geek3 | Uploaded own work with UploadWizard |
File usage
The following page uses this file:
Global file usage
The following other wikis use this file:
- Usage on fa.wikipedia.org
- Usage on sr.wikipedia.org
- Usage on tl.wikipedia.org
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.
If the file has been modified from its original state, some details may not fully reflect the modified file.
| Short title | VFPt_metal_balls_largesmall_potential+contour |
|---|---|
| Image title | VFPt_metal_balls_largesmall_potential+contour
created with VectorFieldPlot 3.1 https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot about: https://commons.wikimedia.org/wiki/File:VFPt_metal_balls_largesmall_potential+contour.svg rights: Creative Commons Attribution ShareAlike 4.0 |
| Width | 800 |
| Height | 600 |