File:VFPt dipoles electric.svg
Original file (SVG file, nominally 840 × 840 pixels, file size: 108 KB)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
| DescriptionVFPt dipoles electric.svg |
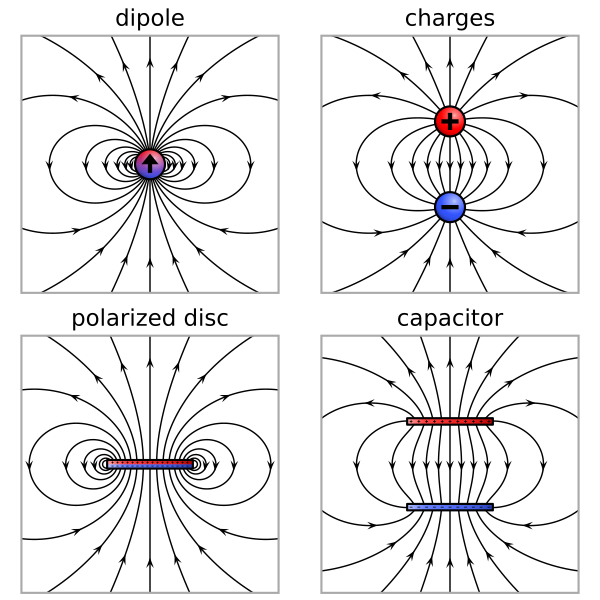
English: Computed drawings of four different types of electric dipoles.
Upper left: An ideal point-like dipole. The field shape is scale invariant and approximates the field of any charge configuration with nonzero dipole moment at large distance. Русский: Рассчитанные электростатические поля четырех различных типов электрических диполей.
Поле идеального точечного диполя. Конфигурация поля в большом масштабе инвариантна и приблизительно соответствует полю любой конфигурации зарядов с ненулевым дипольным моментом на большом расстоянии. Дискретный диполь двух противоположных точечных зарядов разнесенных на конечное расстояние, – физический диполь. Тонкий круглый диск с равномерной электрической поляризацией вдоль оси симметрии. Плоский конденсатор с одинаково заряженными круглыми обкладками. Несмотря на различие этих конфигураций, вблизи которых поля существенно различаются, все эти поля сходятся к одному и тому же дипольному полю на больших расстояниях где они приблизительно одинаковы, при этом любая система зарядов может моделировать идеальный электрический диполь. |
| Date | |
| Source | Own work |
| Author | Geek3 |
| Other versions |
|
| SVG development InfoField | This plot was created with VectorFieldPlot. This file is translated using SVG switch elements: all translations are stored in the same file. |
| Source code InfoField | Python code# paste this code at the end of VectorFieldPlot 3.3
R = 0.6
h = 0.6
rsym = 21
doc = FieldplotDocument('VFPt_dipoles_electric1', commons=True,
width=360, height=360)
field = Field([ ['dipole', {'x':0, 'y':0, 'px':0., 'py':1.}] ])
def f_arrows(xy):
return xy[1] * (sc.hypot(xy[0], xy[1]) / 1.4 - 1)
def f_cond(xy):
return hypot(*xy) > 1e-4 and (fabs(xy[1]) < 1e-3 or fabs(xy[1]) > .3)
nlines = 19
startpoints = Startpath(field, lambda t: 0.25*sc.array([sin(t), cos(t)]),
t0=-pi/2, t1=pi/2).npoints(nlines)
for p0 in startpoints:
line = FieldLine(field, p0, directions='both')
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
# draw dipole symbol
rb_grad = etree.SubElement(doc._get_defs(), 'linearGradient')
rb_grad.set('id', 'grad_rb')
for attr, val in [['x1', '0'], ['x2', '0'], ['y1', '0'], ['y2', '1']]:
rb_grad.set(attr, val)
for col, of in [['#3355ff', '0'], ['#9944aa', '0.5'], ['#ff0000', '1']]:
stop = etree.SubElement(rb_grad, 'stop')
stop.set('stop-color', col)
stop.set('offset', of)
stop.set('stop-opacity', '1')
symb = doc.draw_object('g', {'id':'dipole_symbol',
'transform':'scale({0},{0})'.format(1./doc.unit)})
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym,
'fill':'url(#grad_rb)', 'stroke':'none'}, group=symb)
doc._check_whitespot()
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym,
'fill':'url(#white_spot)', 'stroke':'#000000', 'stroke-width':'3'},
group=symb)
doc.draw_object('path', {'fill':'#000000', 'stroke':'none',
'd':'M 3,-12 V 0 H 12 L 0,15 L -12,0 H -3 V -12 H 3 Z'}, group=symb)
doc.write()
doc = FieldplotDocument('VFPt_dipoles_electric2', commons=True,
width=360, height=360)
field = Field([ ['monopole', {'x':0, 'y':h, 'Q':1}],
['monopole', {'x':0, 'y':-h, 'Q':-1}] ])
def f_arrows(xy):
return xy[1] * (sc.hypot(xy[0], xy[1]) / 1.4 - 1)
def f_cond(xy):
return fabs(xy[0]) < 1.4
nlines = 18
stp = Startpath(field, lambda t: R*sc.array([.2*sin(t), 1+.2*cos(t)]),
t0=-pi, t1=pi)
startpoints = [stp.startpos(s) for s in sc.arange(nlines)/float(nlines)]
startpoints.append(startpoints[nlines//2].dot([[1,0],[0,-1]]))
for p0 in startpoints:
line = FieldLine(field, p0, directions='both', maxr=100)
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
# draw charge symbols
symb_plus = doc.draw_object('g', {
'transform':'translate(0,{0}) scale({1},{1})'.format(h, 1./doc.unit)})
symb_minus = doc.draw_object('g', {
'transform':'translate(0,{0}) scale({1},{1})'.format(-h, 1./doc.unit)})
for i, g in enumerate([symb_plus, symb_minus]):
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym, 'stroke':'none',
'fill':['#ff0000', '#3355ff'][i]}, group=g)
doc._check_whitespot()
doc.draw_object('circle', {'cx':'0', 'cy':'0', 'r':rsym,
'fill':'url(#white_spot)', 'stroke':'#000000', 'stroke-width':'3'}, group=g)
c_symb = doc.draw_object('path', {'fill':'#000000', 'stroke':'none'}, group=g)
if i == 0: # plus sign
c_symb.set('d', 'M 3,3 V 12 H -3 V 3 H -12 V -3'
+ ' H -3 V -12 H 3 V -3 H 12 V 3 H 3 Z')
else: # minus sign
c_symb.set('d', 'M 12,3 H -12 V -3 H 12 V 3 Z')
doc.write()
doc = FieldplotDocument('VFPt_dipoles_electric3', commons=True,
width=360, height=360)
field = Field([ ['ringcurrent', {'x':0, 'y':0, 'R':R, 'phi':pi/2, 'I':1.}] ])
def f_arrows(xy):
return xy[1] * (sc.hypot(xy[0], xy[1]) / 1.4 - 1)
def f_cond(xy):
return hypot(*xy) > 1.2*R and fabs(fabs(xy[0]) - 1.4) > 0.2
nlines = 19
startpoints = Startpath(field, lambda t: sc.array([R*t, 0.]),
t0=-0.9375, t1=0.9375).npoints(nlines)
for p0 in startpoints:
line = FieldLine(field, p0, directions='both')
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
# draw polarized sheet
sheet = doc.draw_object('g', {'id':'polarized_sheet'})
s = 0.06
doc.draw_object('rect', {'x':-R, 'y':-s, 'width':2*R, 'height':2*s,
'stroke':'none', 'fill':'#3355ff'}, group=sheet)
doc.draw_object('rect', {'x':-R, 'y':0, 'width':2*R, 'height':s,
'stroke':'none', 'fill':'#ff0000'}, group=sheet)
grad = doc.draw_object('linearGradient', {'id':'grad-round',
'x1':str(R), 'x2':str(-R), 'y1':'0', 'y2':'0',
'gradientUnits':'userSpaceOnUse'}, group=doc.defs)
for o, c, a in ((0, '#000', 0.3), (0.3, '#999', 0.2),
(0.8, '#fff', 0.25), (1, '#fff', 0.65)):
doc.draw_object('stop', {'id':'grad',
'offset':str(o), 'stop-color':c, 'stop-opacity':str(a)}, grad)
doc.draw_object('rect', {'x':-R, 'y':-s, 'width':2*R, 'height':2*s,
'stroke':'#000000', 'stroke-width':0.03, 'fill':'url(#grad-round)',
'stroke-linejoin':'round'}, group=sheet)
symbols_plus = []
symbols_minus = []
for x in sc.linspace(-R*0.875, R*0.875, 16):
symbols_minus.append('M {:.3f},0 h 0.03'.format(x-0.015))
symbols_plus.append('M {:.3f},0 h 0.03 M {:.3f},-0.015 v 0.03'.format(
x-0.015, x))
doc.draw_object('path', {'d':' '.join(symbols_plus), 'stroke':'#000000',
'fill':'none', 'stroke-width':0.01, 'stroke-linecap':'butt',
'transform':'translate(0,0.025)'}, group=sheet)
doc.draw_object('path', {'d':' '.join(symbols_minus), 'stroke':'#000000',
'fill':'none', 'stroke-width':0.01, 'stroke-linecap':'butt',
'transform':'translate(0,-0.025)'}, group=sheet)
doc.write()
doc = FieldplotDocument('VFPt_dipoles_electric4', commons=True,
width=360, height=360)
field_D = Field([ ['coil', {'x':0, 'y':0, 'phi':pi/2, 'R':R, 'Lhalf':h,
'I':1./(R**2*pi)}] ])
field_E = Field([ ['charged_disc', {'x0':-R, 'x1':R, 'y0':h, 'y1':h, 'Q':.5/h}],
['charged_disc', {'x0':-R, 'x1':R, 'y0':-h, 'y1':-h, 'Q':-.5/h}] ])
field_E_inside = Field([ ['homogeneous', {'Fx':0., 'Fy':-.5/(h*R**2*pi)}],
['coil', {'x':0, 'y':0, 'phi':pi/2, 'R':R, 'Lhalf':h, 'I':1./(R**2*pi)}] ])
def f_arrows(xy):
return xy[1] * (sc.hypot(xy[0], xy[1]) / 1.4 - 1)
def f_cond(xy):
return True
# Use fieldlines in D-field to find good starting points
nlines = 13
startpoints = []
startpoints2 = []
for iline in range(nlines):
p0 = sc.array([R * (-1. + 2. * (iline + 0.5) / nlines), 0.])
print('p0', p0)
line_D = FieldLine(field_D, p0, directions='forward',
maxr=100, stop_funcs=2*[lambda xy: -xy[1] - max(0, 1-hypot(*xy)/R)])
p1 = line_D.nodes[-1]['p']
startpoints.append(p1)
if iline >= 3 and iline < nlines - 3:
line_D = FieldLine(field_D, p0, directions='forward',
maxr=2, stop_funcs=2*[lambda xy: xy[1] - h])
p2 = line_D.nodes[-1]['p']
startpoints2.append(p2)
startpoints.append([0, -3])
for p0 in startpoints:
line = FieldLine(field_E, p0, directions='both', maxr=100)
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
for p0 in startpoints2:
line = FieldLine(field_E_inside, p0, directions='forward',
stop_funcs=2*[lambda xy: -xy[1] - h])
doc.draw_line(line, maxdist=1, arrows_style={'at_potentials':[0.],
'potential':f_arrows, 'condition_func':f_cond, 'scale':1.2})
# draw charged discs
disc_plus = doc.draw_object('g', {'id':'disc_plus',
'transform':'translate(0,{0})'.format(h)})
disc_minus = doc.draw_object('g', {'id':'disc_minus',
'transform':'translate(0,{0})'.format(-h)})
s = 0.045
grad = doc.draw_object('linearGradient', {'id':'grad-round',
'x1':str(R), 'x2':str(-R), 'y1':'0', 'y2':'0',
'gradientUnits':'userSpaceOnUse'}, group=doc.defs)
for o, c, a in ((0, '#000', 0.3), (0.3, '#999', 0.2),
(0.8, '#fff', 0.25), (1, '#fff', 0.65)):
doc.draw_object('stop', {
'offset':str(o), 'stop-color':c, 'stop-opacity':str(a)}, grad)
for i, g in enumerate([disc_plus, disc_minus]):
doc.draw_object('rect', {'x':-R, 'y':-s, 'width':2*R, 'height':2*s,
'stroke':'none', 'fill':['#ff0000', '#3355ff'][i]}, group=g)
doc.draw_object('rect', {'x':-R, 'y':-s, 'width':2*R, 'height':2*s,
'stroke':'#000000', 'stroke-width':0.03, 'fill':'url(#grad-round)',
'stroke-linejoin':'round'}, group=g)
symbols = []
for x in [R * (2 * (0.5 + isy) / 11 - 1) for isy in range(11)]:
if i == 0:
d = 'M {:.3f},0 h 0.04 M {:.3f},-0.02 v 0.04'.format(x-0.02, x)
else:
d = 'M {:.3f},0 h 0.04'.format(x-0.02)
symbols.append(d)
doc.draw_object('path', {'d':' '.join(symbols), 'stroke':'#000000',
'fill':'none', 'stroke-width':0.01, 'stroke-linecap':'butt'}, group=g)
doc.write()
|
Licensing
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Captions
11 January 2020
image/svg+xml
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 21:37, 22 May 2021 |  | 840 × 840 (108 KB) | Geek3 | added russion captions from VFPt_dipoles_electric-ru.svg |
| 16:25, 11 January 2020 |  | 840 × 840 (107 KB) | Geek3 | User created page with UploadWizard |
File usage
The following page uses this file:
Global file usage
The following other wikis use this file:
- Usage on bn.wikipedia.org
- Usage on sk.wikipedia.org
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.
If the file has been modified from its original state, some details may not fully reflect the modified file.
| Short title | VFPt_dipoles_electric |
|---|---|
| Image title | VFPt_dipoles_electric
created with VectorFieldPlot 2.5 https://commons.wikimedia.org/wiki/User:Geek3/VectorFieldPlot about: https://commons.wikimedia.org/wiki/File:VFPt_dipoles_electric.svg rights: Creative Commons Attribution ShareAlike 4.0 |
| Width | 840 |
| Height | 840 |


