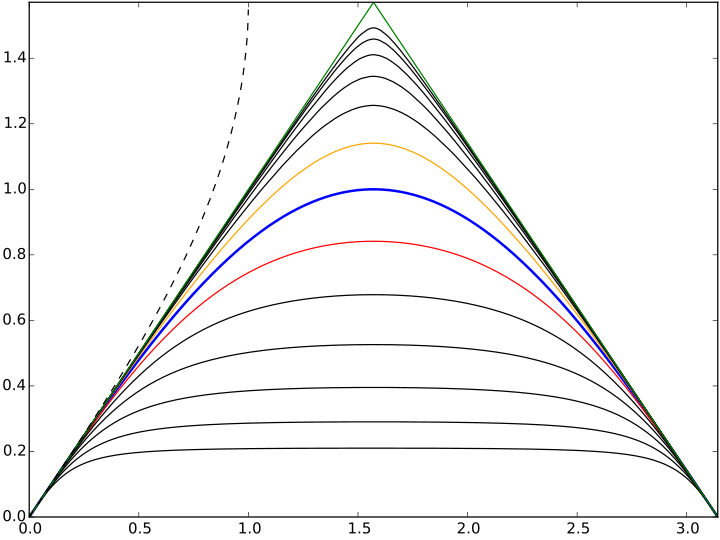
English: Iterates of the sine function (
blue), in the first half-period. Half-iterate (
orange), i.e., the sine's functional square root; the functional square root of that, the quarter-iterate (black) above it, up until the 1/64 iterate; and six integral iterates below it, starting with the second iterate (
red). The
green envelope triangle represents the limiting null iterate, the sawtooth function serving as the starting point leading to the sine function. The dashed black function is iterate -1, or the inverse of sine (arc sine).
Python source code:
import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.linspace(0, np.pi, 10000)
def double_iter(a):
d = np.array(a)
interpolated = interpolate.interp1d(x, a, kind="linear")
for i in range(len(a)):
d[i] = interpolated(min(x[-1], a[i]))
return d
def improve(candidate, f):
improved = np.empty_like(candidate)
for i in range(len(f)):
naive_newval = np.argmin(np.abs(candidate[:len(f)/2]-f[i])) * np.pi/len(f)
improved[i] = candidate[i] + 0.1*(naive_newval - candidate[i])
return improved
def half_iter(f):
half = np.array(f)
mean_error = float("inf")
while mean_error > 1e-4:
half = improve(half, f)
mean_error = np.mean(np.abs(double_iter(half)-f))
print mean_error
return half
iter_1 = np.sin(x)
iter_minus1 = np.arcsin(x)
iter_0 = np.concatenate((x[0:len(x)/2], np.flipud(x[0:len(x)/2])), axis=1)
iter_2 = double_iter(iter_1)
iter_4 = double_iter(iter_2)
iter_8 = double_iter(iter_4)
iter_16 = double_iter(iter_8)
iter_32 = double_iter(iter_16)
iter_64 = double_iter(iter_32)
iter_1_2 = half_iter(iter_1)
iter_1_4 = half_iter(iter_1_2)
iter_1_8 = half_iter(iter_1_4)
iter_1_16 = half_iter(iter_1_8)
iter_1_32 = half_iter(iter_1_16)
iter_1_64 = half_iter(iter_1_32)
n = 10
plotx = x[::n]
plt.plot(plotx, iter_1[::n],"b",linewidth=2)
plt.plot(plotx, iter_2[::n],"r")
plt.plot(plotx, iter_4[::n],"k")
plt.plot(plotx, iter_8[::n],"k")
plt.plot(plotx, iter_16[::n],"k")
plt.plot(plotx, iter_32[::n],"k")
plt.plot(plotx, iter_64[::n],"k")
plt.plot(plotx, iter_1_2[::n],"orange")
plt.plot(plotx, iter_1_4[::n],"k")
plt.plot(plotx, iter_1_8[::n],"k")
plt.plot(plotx, iter_1_16[::n],"k")
plt.plot(plotx, iter_1_32[::n],"k")
plt.plot(plotx, iter_1_64[::n],"k")
plt.plot(plotx, iter_0[::n],"g")
plt.plot(x, iter_minus1,"k--")
plt.ylim([0,np.pi/2])
plt.xlim([0,np.pi])
plt.tight_layout(pad=0.15)
plt.savefig("Sine_iterations.svg")