File:Schwarz triangle function.svg
Page contents not supported in other languages.
Tools
Actions
General
In other projects
Appearance
Size of this PNG preview of this SVG file: 617 × 599 pixels. Other resolutions: 247 × 240 pixels | 494 × 480 pixels | 791 × 768 pixels | 1,055 × 1,024 pixels | 2,109 × 2,048 pixels | 619 × 601 pixels.
Original file (SVG file, nominally 619 × 601 pixels, file size: 222 KB)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
This plot was created with Matplotlib.
| DescriptionSchwarz triangle function.svg |
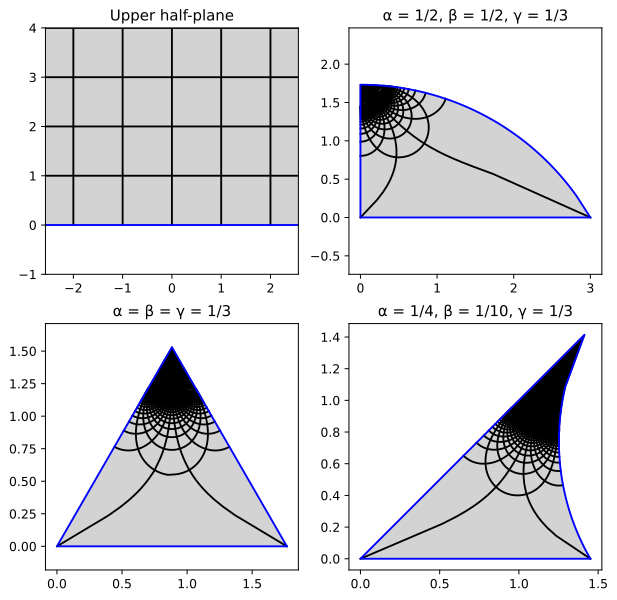
English: Plots of the Schwarz triangle function for various parameters.
|
||
| Date | |||
| Source | Own work | ||
| Author | Apocheir | ||
| Source code InfoField | Python code
|
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
| This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. | |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
Captions
Plots of the Schwarz triangle function
Items portrayed in this file
depicts
16 August 2022
image/svg+xml
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 01:02, 18 August 2022 |  | 619 × 601 (222 KB) | Apocheir | titles, more distinct choice of parameters |
| 02:28, 17 August 2022 |  | 615 × 601 (226 KB) | Apocheir | Uploaded own work with UploadWizard |
File usage
The following page uses this file:
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.
If the file has been modified from its original state, some details may not fully reflect the modified file.
| Width | 495.008017pt |
|---|---|
| Height | 481.15125pt |
Retrieved from "https://en.wikipedia.org/wiki/File:Schwarz_triangle_function.svg"
