File:Double six.svg
Appearance
Size of this PNG preview of this SVG file: 622 × 599 pixels. Other resolutions: 249 × 240 pixels | 498 × 480 pixels | 797 × 768 pixels | 1,063 × 1,024 pixels | 2,125 × 2,048 pixels | 635 × 612 pixels.
Original file (SVG file, nominally 635 × 612 pixels, file size: 14 KB)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 03:59, 3 January 2017 |  | 635 × 612 (14 KB) | Hedwig in Washington | Reverted to version as of 23:29, 31 July 2010 (UTC) |
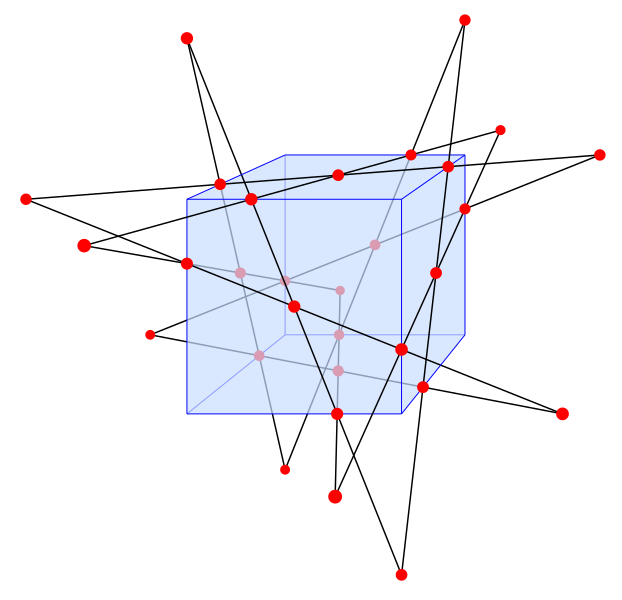
| 23:29, 31 July 2010 |  | 635 × 612 (14 KB) | David Eppstein | {{Information |Description={{en|1=Schläfli's double six configuration — twelve lines with five intersection points per line and two lines per intersection point, intersecting in the pattern of a crown graph — inscribed on a cube, |
File usage
The following 3 pages use this file:
Global file usage
The following other wikis use this file:
- Usage on ru.wikipedia.org
- Usage on uk.wikipedia.org

