File:Birthdaymatch.svg
Page contents not supported in other languages.
Tools
Actions
General
In other projects
Appearance
Size of this PNG preview of this SVG file: 720 × 540 pixels. Other resolutions: 320 × 240 pixels | 640 × 480 pixels | 1,024 × 768 pixels | 1,280 × 960 pixels | 2,560 × 1,920 pixels.
Original file (SVG file, nominally 720 × 540 pixels, file size: 291 KB)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
| DescriptionBirthdaymatch.svg |
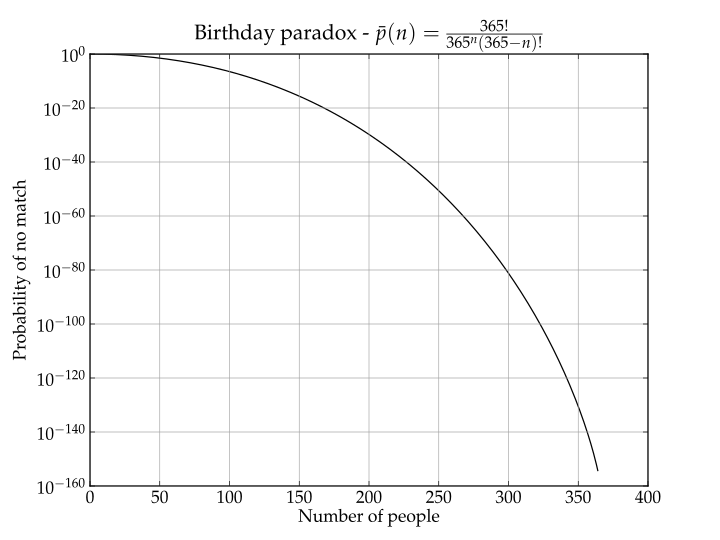
English: In probability theory, the birthday problem or birthday paradox concerns the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 367 (since there are 366 possible birthdays, including February 29). However, 99% probability is reached with just 57 people, and 50% probability with 23 people. These conclusions are based on the assumption that each day of the year (except February 29) is equally probable for a birthday.
The mathematics behind this problem led to a well-known cryptographic attack called the birthday attack, which uses this probabilistic model to reduce the complexity of cracking a hash function. |
| Date | |
| Source | Own work |
| Author | Guillaume Jacquenot |
| SVG development InfoField | This W3C-invalid plot was created with Matplotlib. |
| Source code InfoField | Python code# -*- coding: utf-8 -*-
#
# Script to generate in English and French, graphs for the
# birthday problem.
# More precisely, it generates two SVG files representing the
# probability of no match of two identical birthday one the same
# wrt the number of person in the considered group.
#
# **************************************************************
# http://en.wikipedia.org/wiki/Birthday_problem
# From Wikipedia, the free encyclopedia:
# In probability theory, the birthday problem or birthday
# paradox concerns the probability that, in a set of n
# randomly chosen people, some pair of them will have the
# same birthday. By the pigeonhole principle, the probability
# reaches 100% when the number of people reaches 367
# (since there are 366 possible birthdays, including February
# 29). However, 99% probability is reached with just 57 people,
# and 50% probability with 23 people. These conclusions are
# based on the assumption that each day of the year (except
# February 29) is equally probable for a birthday.
#
# The mathematics behind this problem led to a well-known
# cryptographic attack called the birthday attack, which
# uses this probabilistic model to reduce the complexity
# of cracking a hash function.
#
# Text under the
# Creative Commons Attribution-ShareAlike License
# **************************************************************
#
# Implementation:
# To ensure numerical accuracy, one evaluates the log10 of the
# probabibity of no match. This allows to converts the
# probability formula from a product formula to a sum formula.
#
#
# Guillaume Jacquenot
# 2013/03/10
import matplotlib.pyplot as plt
from matplotlib import rc
rc('font',**{'family':'serif','serif':['Palatino'],'size':14})
rc('text', usetex=True)
import numpy as np
def BirthdaymatchComputationLog10():
'''
This function evaluates the log10 probability of no
match for the birthday paradox.
This ensures no approximation on the result.
$\log _{10} \left( {\bar p(n)} \right) =
\sum\limits_{i = 365 + 1 - n}^{365}
{\log _{10} \left( i \right)}
- n\log _{10} \left( {365} \right)$
'''
n=np.arange(1,365)
nR=np.arange(365,1,-1)
p=np.cumsum(np.log10(nR))-n*np.log10(365)
return n,p
def BirthdaymatchGenerateTitle(logTitle=False):
if logTitle:
title='$\\log _{10} \\left( {\\bar p(n)} \\right)\
= \\sum\\limits_{i = 365 + 1 - n}^{365}\
{\\log _{10} \\left( i \\right)}\
- n\\log _{10} \\left( {365} \\right)$'
else:
title='$\\bar p(n) = \\frac{365!}{365^n\
\\left( {365 - n} \\right)!}$'
return title
def Birthdaymatch(\
labels={'xlabel':'Number of people',\
'ylabel':'Probability of no match',\
'title':'Birthday paradox'},\
outputFilename = r'Birthdaymatch.svg'):
n,p = BirthdaymatchComputationLog10()
fig, ax = plt.subplots()
plt.plot(n,p,c='k', linestyle='-')
plt.grid(True, ls='-', c='#a0a0a0')
plt.xlabel(labels['xlabel'])
plt.ylabel(labels['ylabel'])
plt.title(labels['title']+' - '+BirthdaymatchGenerateTitle())
fig.canvas.draw()
labels = [item.get_text() for item in ax.get_yticklabels()]
labels = [label[1:] if label.startswith('$') else label for label in labels]
labels = [label[0:-1] if label.endswith('$') else label for label in labels]
labels = ['$10^{'+label+'}$' for label in labels]
ax.set_yticklabels(labels)
plt.savefig(outputFilename)
Birthdaymatch()
Birthdaymatch(\
labels={'xlabel':u"Nombre de personnes",\
'ylabel':u"Probabilit\\'e de non correspondance",\
'title':u"Paradoxe des anniversaires"},\
outputFilename = r'Birthdaymatch_FR.svg')
|
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Captions
Add a one-line explanation of what this file represents
Items portrayed in this file
depicts
10 March 2013
image/svg+xml
68b9c96e2a245296ec08bbfe7963536985e6cf9e
297,936 byte
540 pixel
720 pixel
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 19:39, 10 March 2013 |  | 720 × 540 (291 KB) | Gjacquenot | User created page with UploadWizard |
File usage
The following 2 pages use this file:
Global file usage
The following other wikis use this file:
- Usage on fa.wikipedia.org
- Usage on fr.wikisource.org
- Usage on ml.wikipedia.org
- Usage on sq.wikipedia.org
- Usage on th.wikipedia.org
- Usage on tr.wikipedia.org
Metadata
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.
If the file has been modified from its original state, some details may not fully reflect the modified file.
| Width | 576pt |
|---|---|
| Height | 432pt |
Retrieved from "https://en.wikipedia.org/wiki/File:Birthdaymatch.svg"
