# -*- coding: utf-8 -*-
#
# Script to generate in English and French, graphs for the
# birthday problem.
#
# **************************************************************
# http://en.wikipedia.org/wiki/Birthday_problem
# From Wikipedia, the free encyclopedia:
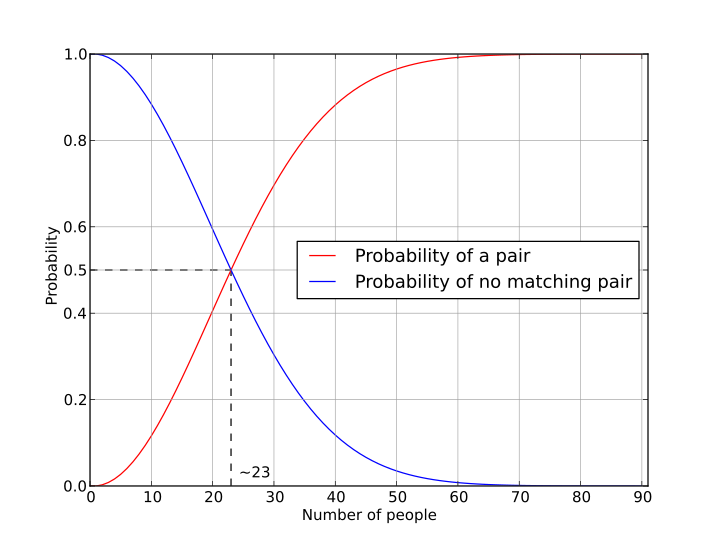
# In probability theory, the birthday problem or birthday
# paradox concerns the probability that, in a set of n
# randomly chosen people, some pair of them will have the
# same birthday. By the pigeonhole principle, the probability
# reaches 100% when the number of people reaches 367
# (since there are 366 possible birthdays, including February
# 29). However, 99% probability is reached with just 57 people,
# and 50% probability with 23 people. These conclusions are
# based on the assumption that each day of the year (except
# February 29) is equally probable for a birthday.
#
# The mathematics behind this problem led to a well-known
# cryptographic attack called the birthday attack, which
# uses this probabilistic model to reduce the complexity
# of cracking a hash function.
#
# Text under the
# Creative Commons Attribution-ShareAlike License
# **************************************************************
#
#
# Guillaume Jacquenot
# 2012/12/16
from pylab import *
import numpy as np
def makePlot(
generateEnglishPlot = True,
outputFilename = r'Birthday_paradox.svg',
useYLogScale = False):
N=91
n = np.arange(float(N))
pbar=np.exp(-n* (n-1) / (2.0*365.0))
p=1.0-pbar
n05 = 0.5*(1.0+np.sqrt(1-8.0*365.0*np.log(1.0-0.5)))
plot([n05,n05],[0.0,0.5],c='k', linestyle='--')
plot([0.0,n05],[0.5,0.5],c='k', linestyle='--')
text(23.5,0.02,' ~23')
if generateEnglishPlot:
plot(n,p ,c='r',label = unicode('Probability of a pair', 'utf8'))
plot(n,pbar,c='b',label = unicode('Probability of no matching pair', 'utf8'))
else:
plot(n,p ,c='r',label = unicode('Probabilité de coïncidence', 'utf8'))
plot(n,pbar,c='b',label = unicode('Probabilité de non-coïncidence', 'utf8'))
legend(loc='right')
xlim(0, N)
if useYLogScale:
ylim(1e-6, 1)
ax = gca()
ax.set_yscale('log')
else:
ylim(0, 1)
yticks([0.0,0.2,0.4,0.5,0.6,0.8,1.0])
xticks(range(0, N, 10))
grid(True, ls='-', c='#a0a0a0')
if generateEnglishPlot:
xlabel('Number of people')
ylabel('Probability')
else:
xlabel('Nombre de personnes')
ylabel(unicode('Probabilité', 'utf8'))
savefig(outputFilename)
show()
makePlot(generateEnglishPlot = True, outputFilename = r'Birthday_paradox.svg')
makePlot(generateEnglishPlot = False, outputFilename = r'Paradoxe_anniversaire.svg')