File:Bifurcation1-2.png
Original file (1,072 × 621 pixels, file size: 21 KB, MIME type: image/png)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Contents
Summary
| DescriptionBifurcation1-2.png |
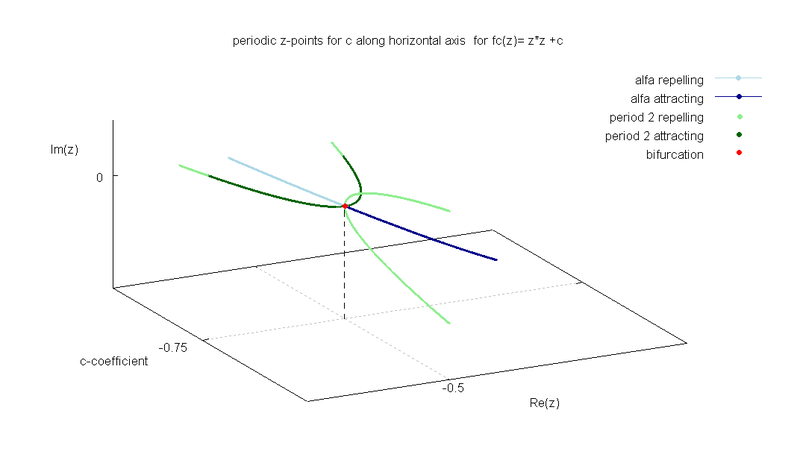
English: Bifurcation of periodic points from period 1 to 2 for fc(z)=z*z +c. Parabolic parameter c = -3/4 and fixed point z = 1/2 |
| Date | |
| Source | Own work |
| Author | Adam majewski |
| Other versions |
|
Summary
This image shows some features of the discrete dynamical system
based on complex quadratic polynomial :
.
When coefficient 
This path is inside Mandelbrot set ( escape route). It s also first of period doubling bifurcation.
Note that :
- there are fixed points for all c values, but they change from attracting to indifferent( in parabolic point, root point) and repelling
- there are 2 period 2 points for all c values. They also change from from attracting to indifferent( in parabolic point, root point) and repelling.
- in bifurcation point ( root, parabolic) all period 2 values and fixed point have the same value and the same (=1) stability index .
- before and after bifurcation point period 2 points creates 3D parabolas, which are rotated ( 90 degrees) with respect to themselves
| stability index of period 1 points | period 1 points on dynamic plane | period 1 points on parameter plane |
|---|---|---|
| changes from attractive through indifferent to repelling | moves from interior of Kc to its boundary | moves from interior of component of M-set to its boundary |
Please check demo 2 page 3 from program Mandel by Wolf Jung to see another visualisation of this bifurcation.
dynamics
| parameter c | location of c | Julia set | interior | type of critical orbit dynamics | critical point | fixed points | stability of alfa |
|---|---|---|---|---|---|---|---|
| c = -3/4 | boundary, root point | connected | exist | parabolic | attracted to alfa fixed point | alfa fixed point equal to beta fixed point, both are parabolic | r = 1 |
| 0 < x < -3/4 | internla ray 1/2 | connected | exist | attracting | attracted to alfa fixed point | 0 < r < 1.0 | |
| c = 0 | center, interior | connected = Circle Julia set | exist | superattracting | attracted to alfa fixed point | fixed critical point equal to alfa fixed point, alfa is superattracting, beta is repelling | r = 0 |
| 0<c<1/4 | internal ray 0, interior | connected | exist | attracting | attracted to alfa fixed point | alfa is attracting, beta is repelling | 0 < r < 1.0 |
| c = 1/4 | cusp, boundary | connected = cauliflower | exist | parabolic | equal to alfa fixed point | alfa fixed point equal to beta fixed point, both are parabolic | r = 1 |
| c>1/4 | external ray 0, exterior | disconnected = imploded cauliflower | disappears | repelling | repelling to infinity | both finite fixed points are repelling | r > 1 |
Stability r is absolute value of multiplier m at fixed point alfa 

c = 0.0000000000000000+0.0000000000000000*I m(c) = 0.0000000000000000+0.0000000000000000*I r(m) = 0.0000000000000000 t(m) = 0.0000000000000000 period = 1
c = 0.0250000000000000+0.0000000000000000*I m(c) = 0.0513167019494862+0.0000000000000000*I r(m) = 0.0513167019494862 t(m) = 0.0000000000000000 period = 1
c = 0.0500000000000000+0.0000000000000000*I m(c) = 0.1055728090000841+0.0000000000000000*I r(m) = 0.1055728090000841 t(m) = 0.0000000000000000 period = 1
c = 0.0750000000000000+0.0000000000000000*I m(c) = 0.1633399734659244+0.0000000000000000*I r(m) = 0.1633399734659244 t(m) = 0.0000000000000000 period = 1
c = 0.1000000000000000+0.0000000000000000*I m(c) = 0.2254033307585166+0.0000000000000000*I r(m) = 0.2254033307585166 t(m) = 0.0000000000000000 period = 1
c = 0.1250000000000000+0.0000000000000000*I m(c) = 0.2928932188134524+0.0000000000000000*I r(m) = 0.2928932188134524 t(m) = 0.0000000000000000 period = 1
c = 0.1500000000000000+0.0000000000000000*I m(c) = 0.3675444679663241+0.0000000000000000*I r(m) = 0.3675444679663241 t(m) = 0.0000000000000000 period = 1
c = 0.1750000000000000+0.0000000000000000*I m(c) = 0.4522774424948338+0.0000000000000000*I r(m) = 0.4522774424948338 t(m) = 0.0000000000000000 period = 1
c = 0.2000000000000000+0.0000000000000000*I m(c) = 0.5527864045000419+0.0000000000000000*I r(m) = 0.5527864045000419 t(m) = 0.0000000000000000 period = 1
c = 0.2250000000000000+0.0000000000000000*I m(c) = 0.6837722339831620+0.0000000000000000*I r(m) = 0.6837722339831620 t(m) = 0.0000000000000000 period = 1
c = 0.2500000000000000+0.0000000000000000*I m(c) = 0.9999999894632878+0.0000000000000000*I r(m) = 0.9999999894632878 t(m) = 0.0000000000000000 period = 1
c = 0.2750000000000000+0.0000000000000000*I m(c) = 1.0000000000000000+0.3162277660168377*I r(m) = 1.0488088481701514 t(m) = 0.0487455572605341 period = 1
c = 0.3000000000000000+0.0000000000000000*I m(c) = 1.0000000000000000+0.4472135954999579*I r(m) = 1.0954451150103321 t(m) = 0.0669301182003075 period = 1
c = 0.3250000000000000+0.0000000000000000*I m(c) = 1.0000000000000000+0.5477225575051662*I r(m) = 1.1401754250991381 t(m) = 0.0797514300099943 period = 1
c = 0.3500000000000000+0.0000000000000000*I m(c) = 1.0000000000000000+0.6324555320336760*I r(m) = 1.1832159566199232 t(m) = 0.0897542589928440 period = 1
==Maxima CAS src code==
<pre>
GiveRoots_bf(g):=
block(
[cc:bfallroots(expand(g)=0)],
cc:map(rhs,cc),/* remove string "c=" */
return(cc)
)$
/* functions for computing periodic points ; */
give_beta(_c):= (1+sqrt(abs(1-4*_c)))/2 $
give_alfa(_c):= (1-sqrt(abs(1-4*_c)))/2 $
give_2(c):=
block(
[eq,rr],
eq:z*z +z +c +1,
rr:GiveRoots_bf(eq),
return(float(rr))
);
xMax:0;
xMin:-1.39;
yMin:-2;
yMax:2;
iXmax:1000;
dx:(xMax-xMin)/iXmax;
/* points */
p_pts:[ [-0.75,-0.5,0] ];
p1_beta:[];
p1_alfa_r:[];
p1_alfa_a:[];
p2_r:[]; /* period 2 repelling */
p2_a:[]; /* period 2 attracting */
/* -------------------- main ----------------------- */
for c:xMin step dx thru xMax do
(
alfa:give_alfa(c),
if cabs(2*alfa)>1
then p1_alfa_r:cons([c,realpart(alfa),imagpart(alfa)],p1_alfa_r)
else p1_alfa_a:cons([c,realpart(alfa),imagpart(beta)],p1_alfa_a),
roots:allroots(z*z +z +c +1=0),
z2:rhs(roots[1]),
if cabs(float(4*z2*(z2*z2+c)))>1 /* multiplier */
then for z in roots do p2_r:cons([c,realpart(rhs(z)),imagpart(rhs(z))],p2_r)
else for z in roots do p2_a:cons([c,realpart(rhs(z)),imagpart(rhs(z))],p2_a)
);
load(cpoly); /* for bfallroots */
load(draw);
draw3d(
terminal = screen,
pic_height= iXmax,
title = "periodic z-points for c along horizontal axis for fc(z)= z*z +c ",
ylabel = "Re(z)",
zlabel ="Im(z)",
xlabel = "c-coefficient",
yrange = [yMin,yMax],
point_type = filled_circle,
point_size = 0.2,
points_joined = true,
/* period 1 */
key = " alfa repelling",
color = dark-blue,
points(p1_alfa_r),
key = " alfa attracting",
color = light-blue,
points(p1_alfa_a),
/* period 2 */
points_joined = false,
key = " period 2 attracting",
color = dark-green,
points(p2_a),
key = " period 2 repelling",
color = light-green,
points(p2_r),
/* grid and tics */
xtics = {-3/4},
/* -2,root points,centers, 0 */
/*xtics_axis = true, plot tics on x-axis */
xtics_rotate = true,
ytics = {-0.5},
ztics = {-1,0,1},
grid = true, /* draw grid*/
/* special points */
point_size = 0.7,
color = red,
key = "bifurcation",
points(p_pts)
)$
Licensing
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.

|
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
Captions
Items portrayed in this file
depicts
some value
20 June 2009
image/png
8bd7df451e38bf38d308f876ff31279f6d84928f
21,244 byte
621 pixel
1,072 pixel
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 16:41, 22 June 2009 |  | 1,072 × 621 (21 KB) | Soul windsurfer | I have changed colors |
| 20:15, 20 June 2009 |  | 1,072 × 621 (21 KB) | Soul windsurfer | {{Information |Description={{en|1=Bifurcation of periodic points from period 1 to 2 for fc(z)=z*z +c}} |Source=Own work by uploader |Author=Adam majewski |Date=2009.06.20 |Permission= |other_versions= }} <!--{{ImageUpload|full}}--> |
File usage
The following 3 pages use this file:
Global file usage
The following other wikis use this file:
- Usage on el.wikipedia.org
- Usage on en.wikibooks.org
- Fractals/Iterations in the complex plane/parabolic
- Fractals/Iterations in the complex plane/Parameter plane
- Fractals/Mathematics/sequences
- Fractals/Iterations in the complex plane/periodic points
- Fractals/Iterations in the complex plane/1over2 family
- Fractals/Mathematics/periodic points of complex quadratic map
- Fractals/Iterations in the complex plane/petal
- Usage on uk.wikipedia.org






