Catalan solid


The Catalan solids are the dual polyhedra of Archimedean solids. The Archimedean solids are thirteen highly-symmetric polyhedra with regular faces and symmetric vertices.[1] The faces of the Catalan solids correspond by duality to the vertices of by Archimedean solids, and vice versa.[2] One way to construct the Catalan solids is by using the Dorman Luke construction.[3]
The Catalan solids are face-transitive or isohedral meaning that their faces are symmetric to one another, but they are not vertex-transitive because their vertices are not symmetric. Their dual, the Archimedean solids, are vertex-transitive but not face-transitive. Each Catalan solid has constant dihedral angles, meaning the angle between any two adjacent faces is the same.[1] Additionally, two Catalan solids, the rhombic dodecahedron and rhombic triacontahedron, are edge-transitive, meaning their edges are symmetric to each other.[citation needed] Some Catalan solids were discovered by Johannes Kepler during his study of zonohedra, and Eugene Catalan completed the list of the thirteen solids in 1865.[4]
Two Catalan solids, the pentagonal icositetrahedron and the pentagonal hexecontahedron, are chiral, meaning that these two solids are not their own mirror images. They are dual to the snub cube and snub dodecahedron respectively, which are also chiral.
Eleven of the thirteen Catalan solids are known to have the Rupert property that a copy of the same solid can be passed through a hole in the solid.[5]
| Name | Image | Faces | Edges | Vertices | Dihedral angle[6] | Point group |
|---|---|---|---|---|---|---|
| triakis tetrahedron | 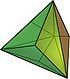
|
12 isosceles triangles | 18 | 8 | 129.521° | Td |
| rhombic dodecahedron | 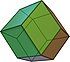
|
12 rhombi | 24 | 14 | 120° | Oh |
| triakis octahedron | 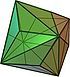
|
24 isosceles triangles | 36 | 14 | 147.350° | Oh |
| tetrakis hexahedron | 
|
24 isosceles triangles | 36 | 14 | 143.130° | Oh |
| deltoidal icositetrahedron | 
|
24 kites | 48 | 26 | 138.118° | Oh |
| disdyakis dodecahedron | 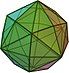
|
48 scalene triangles | 72 | 26 | 155.082° | Oh |
| pentagonal icositetrahedron | 
|
24 pentagons | 60 | 38 | 136.309° | O |
| rhombic triacontahedron | 
|
30 rhombi | 60 | 32 | 144° | Ih |
| triakis icosahedron | 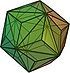
|
60 isosceles triangles | 90 | 32 | 160.613° | Ih |
| pentakis dodecahedron | 
|
60 isosceles triangles | 90 | 32 | 156.719° | Ih |
| deltoidal hexecontahedron | 
|
60 kites | 120 | 62 | 154.121° | Ih |
| disdyakis triacontahedron | 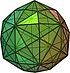
|
120 scalene triangles | 180 | 62 | 164.888° | Ih |
| pentagonal hexecontahedron | 
|
60 pentagons | 150 | 92 | 153.179° | I |
References
[edit]Footnotes
[edit]- ^ a b Diudea (2018), p. 39.
- ^ Wenninger (1983), p. 1, Basic notions about stellation and duality.
- ^
- Cundy & Rollett (1961), p. 117
- Wenninger (1983), p. 30
- ^
- Diudea (2018), p. 39
- Heil & Martini (1993), p. 352
- ^ Fredriksson (2024).
- ^ Williams (1979).
Works cited
[edit]- Cundy, H. Martyn; Rollett, A. P. (1961), Mathematical Models (2nd ed.), Oxford: Clarendon Press, MR 0124167.
- Diudea, M. V. (2018), Multi-shell Polyhedral Clusters, Carbon Materials: Chemistry and Physics, vol. 10, Springer, doi:10.1007/978-3-319-64123-2, ISBN 978-3-319-64123-2.
- Fredriksson, Albin (2024), "Optimizing for the Rupert property", The American Mathematical Monthly, 131 (3): 255–261, arXiv:2210.00601, doi:10.1080/00029890.2023.2285200.
- Gailiunas, P.; Sharp, J. (2005), "Duality of polyhedra", International Journal of Mathematical Education in Science and Technology, 36 (6): 617–642, doi:10.1080/00207390500064049, S2CID 120818796.
- Heil, E.; Martini, H. (1993), "Special convex bodies", in Gruber, P. M.; Wills, J. M. (eds.), Handbook of Convex Geometry, North Holland, ISBN 978-0-08-093439-6
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
External links
[edit]- Weisstein, Eric W. "Catalan Solids". MathWorld.
- Weisstein, Eric W. "Isohedron". MathWorld.
- Catalan Solids – at Visual Polyhedra
- Archimedean duals – at Virtual Reality Polyhedra
- Interactive Catalan Solid in Java
- Download link for Catalan's original 1865 publication – with beautiful figures, PDF format
















































