Bürgi–Dunitz angle

Bürgi–Dunitz and Flippin–Lodge nucleophile approach trajectory angles, $\alpha _{BD}$ and $\alpha _{FL}$, analogized to altitude- and azimuth-types of parameters in the celestial (horizontal) coordinate system. Both in this celestial coordinate system, and in the system to describe a nucleophile approaching a planar electrophile, the problem is to uniquely describe the location of a point off of a plane, relative to specific point on the plane. Hence, in both cases, the problem can be addressed using two angles, an altitude-type angle and an azimuth-type angle. Note, while elevation in celestial applications is most easily measured as the specific altitude shown, the elevation of the nucleophile, $\alpha _{BD}$, is most easily measured as the supplementary angle, Nu-C-O, hence its values are most often >90° (see text and next image).

The Bürgi–Dunitz angle (BD angle) is one of two angles that fully define the geometry of "attack" (approach via collision) of a nucleophile on a trigonal unsaturated center in a molecule, originally the carbonyl center in an organic ketone, but now extending to aldehyde, ester, and amide carbonyls, and to alkenes (olefins) as well. The angle was named after crystallographers Hans-Beat Bürgi and Jack D. Dunitz, its first senior investigators.

Practically speaking, the Bürgi–Dunitz and Flippin–Lodge angles were central to the development of understanding of chiral chemical synthesis, and specifically of the phenomenon of asymmetric induction during nucleophilic attack at hindered carbonyl centers (see the Cram–Felkin–Anh and Nguyen models).

Additionally, the stereoelectronic principles that underlie nucleophiles adopting a proscribed range of Bürgi–Dunitz angles may contribute to the conformational stability of proteins and are invoked to explain the stability of particular conformations of molecules in one hypothesis of a chemical origin of life.

Definition

In the addition of a nucleophile (Nu) attack to a carbonyl, the BD angle is defined as the Nu-C-O bond angle. The BD angle adopted during an approach by a nucleophile to a trigonal unsaturated electrophile depends primarily on the molecular orbital (MO) shapes and occupancies of the unsaturated carbon center (e.g., carbonyl center), and only secondarily on the molecular orbitals of the nucleophile.

Of the two angles which define the geometry of nucleophilic "attack", the second describes the "offset" of the nucleophile's approach toward one of the two substituents attached to the carbonyl carbon or other electrophilic center, and was named the Flippin–Lodge angle (FL angle) by Clayton Heathcock after his contributing collaborators Lee A. Flippin and Eric P. Lodge.

These angles are generally construed to mean the angle measured or calculated for a given system, and not the historically observed value range for the original Bürgi–Dunitz aminoketones, or an idealized value computed for a particular system (such as hydride addition to formaldehyde, image at left). That is, the BD and FL angles of the hydride-formaldehyde system produce a given pair of values, while the angles observed for other systems may vary relative to this simplest of chemical systems.

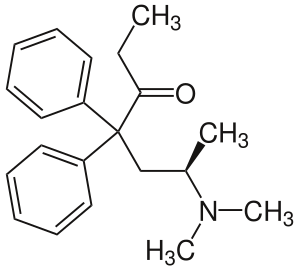
Measurement

The original Bürgi-Dunitz measurements were of a series of intramolecular amine-ketone carbonyl interactions, in crystals of compounds bearing both functionalities—e.g., methadone and protopine. These gave a narrow range of BD angle values (105 ± 5°); corresponding computations—molecular orbital calculations of the SCF-LCAO-type—describing the approach of the s-orbital of a hydride anion (H⁻) to the pi-system of the simplest aldehyde, formaldehyde (H₂C=O), gave a BD angle value of 107°.

Hence, Bürgi, Dunitz, and thereafter many others noted that the crystallographic measurements of the aminoketones and the computational estimate for the simplest nucleophile-electrophile system were quite close to a theoretical ideal, the tetrahedral angle (internal angles of a tetrahedron, 109.5°), and so consistent with a geometry understood to be important to developing transition states in nucleophilic attacks at trigonal centers.

• 
  Structure of L-methadone, a key molecule whose crystals were studied in the development of the BD angle concept.
• 
  Structure of protopine, an alkaloid, whose crystals were also studied in the development of the BD angle concept.
• 
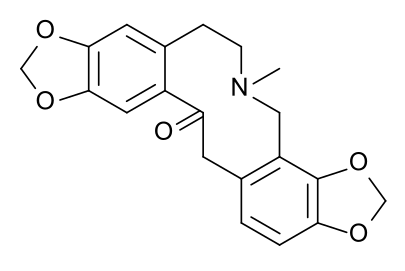
  The amine-to-carbonyl n→π* interaction in protopine with an unusually short N···C distance of 2.555 Å and a Bürgi–Dunitz angle of 102°.

In the structure of L-methadone (above, left), note the tertiary amine projecting to the lower right, and the carbonyl (C=O) group at the center, which engage in an intramolecular interaction in the crystal structure (after rotation around the single bonds connecting them, during the crystallization process).

Similarly, in the structure of protopine (above, center), note the tertiary amine at the center of the molecule, part of a ten-membered ring, and the C=O group opposite it on the ring; these engage in an intramolecular interaction allowed by changes in the torsion angles of the atoms of the ring.

Theory

Hydride addition to formaldehyde

Estimated Bürgi–Dunitz ($\alpha _{BD}$) angle for this simplest H^(–) → H₂C=O nucleo-philic addition.

HOMO-LUMO interaction underlying $\alpha _{BD}$ angle in simple systems.

(Left) Shown is nucleophilic attack by the charged nucleophile (Nu), hydride anion, on the unsaturated trigonal center of the aldehyde electrophile, formaldehyde (R,R'=H). The value computed as optimal for this system, 107°, is indicated, and is representative of the obtuse values observed in most experimental chemical systems.
(Right) Cartoon of the approach of a p-type highest occupied molecular orbital (HOMO) of a nucleophile such as chloride ion (green sphere), and the lowest unoccupied molecular orbital (LUMO) of the trigonal center of an electrophilic carbonyl of formaldehyde (black sphere carbon, red sphere oxygen, white spheres hydrogen). View is nearly side on, and the developing out-of-plane distortion of the carbonyl carbon atom is omitted for simplicity.

The convergence of observed BD angles can be viewed as arising from the need to maximize overlap between the highest occupied molecular orbital (HOMO) of the nucleophile, and the lowest unoccupied molecular orbital (LUMO) of the unsaturated, trigonal center of the electrophile. (See, in comparison, the related inorganic chemistry concept of the angular overlap model.)

In the case of addition to a carbonyl, the HOMO is often a p-type orbital (e.g., on an amine nitrogen or halide anion), and the LUMO is generally understood to be the antibonding π* molecular orbital perpendicular to the plane containing the ketone C=O bond and its substituents (see figure at right above). The BD angle observed for nucleophilic attack is believed to approach the angle that would produce optimal overlap between HOMO and LUMO (based on the principle of the lowering of resulting new molecular orbital energies after such mixing of orbitals of similar energy and symmetry from the participating reactants). At the same time, the nucleophile avoids overlap with other orbitals of the electrophilic group that are unfavorable for bond formation (not apparent in image at right, above, because of the simplicity of the R=R'=H in formaldehyde).

Complications

Electrostatic and Van der Waals interactions

To understand cases of real chemical reactions, the HOMO-LUMO-centered view is modified by understanding of further complex, electrophile-specific repulsive and attractive electrostatic and Van der Waals interactions that alter the altitudinal BD angle, and bias the azimuthal Flippin-Lodge angle toward one substituent or the other (see graphic above).

Linear and rotational dynamics

BD angle theory was developed based on "frozen" interactions in crystals where the impacts of dynamics at play in the system (e.g., easily changed torsional angles) may be negligible. However, much of the chemistry of general interest and use takes place via collisions of molecules tumbling in solution; accordingly, dynamics are taken into account in such cases.

Constrained environments in enzymes and nanomaterials

Moreover, in constrained reaction environments such as in enzyme and nanomaterial binding sites, early evidence suggests that BD angles for reactivity can be quite distinct, since reactivity concepts assuming orbital overlaps during random collision are not directly applicable.

For instance, the BD value determined for enzymatic cleavage of an amide by a serine protease (subtilisin) was 88°, quite distinct from the hydride-formaldehyde value of 107°; moreover, compilation of literature crystallographic BD angle values for the same reaction mediated by different protein catalysts clustered at 89 ± 7° (i.e., only slightly offset from directly above or below the carbonyl carbon). At the same time, the subtilisin FL value was 8°, and FL angle values from the careful compilation clustered at 4 ± 6° (i.e., only slightly offset from directly behind the carbonyl; see the Flippin–Lodge angle article).

See also

• Flippin–Lodge angle